6.1 What is a Tree?
A tree is a data structure similar to a linked list but instead of each node pointing simply to the next node in a linear fashion, each node points to a number of nodes. Tree is an example of a nonlinear data structure. A tree structure is a way of representing the hierarchical nature of a structure in a graphical form.
In trees ADT (Abstract Data Type), the order of the elements is not important. If we need ordering information, linear data structures like linked lists, stacks, queues, etc. can be used.
6.2 Glossary
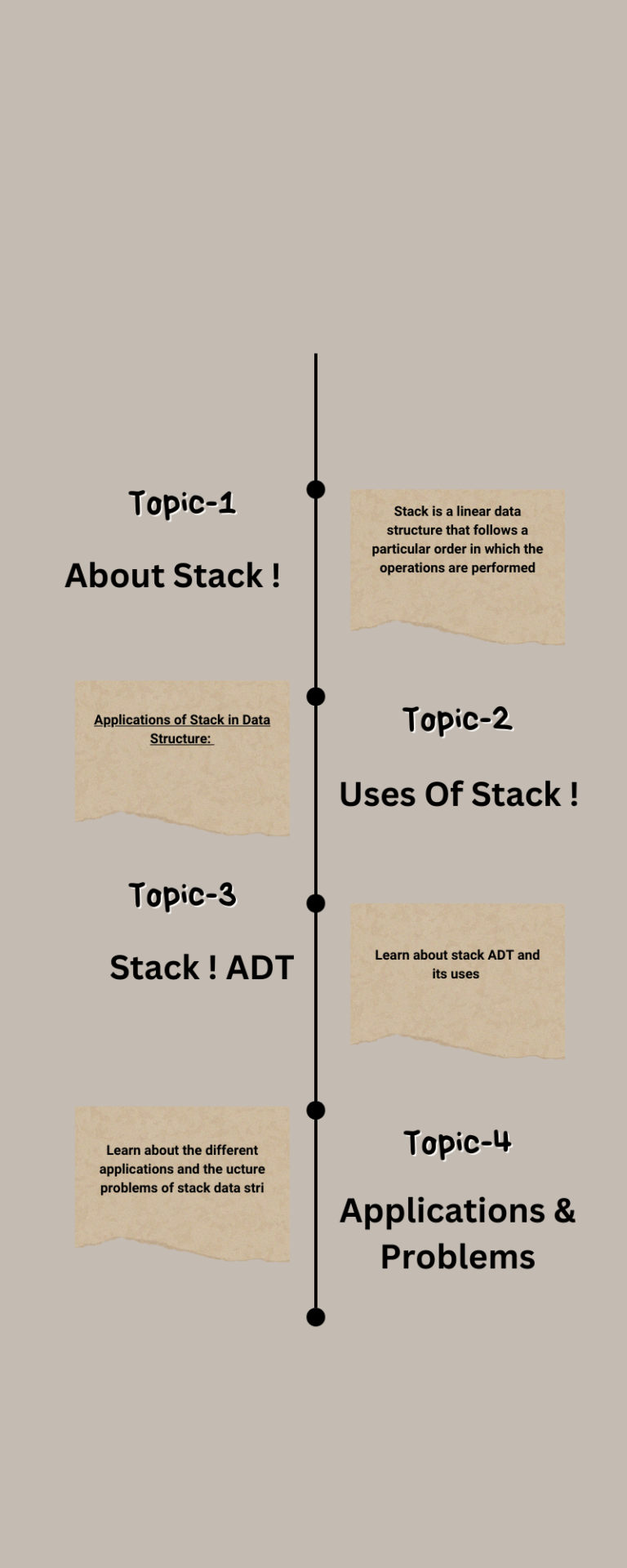
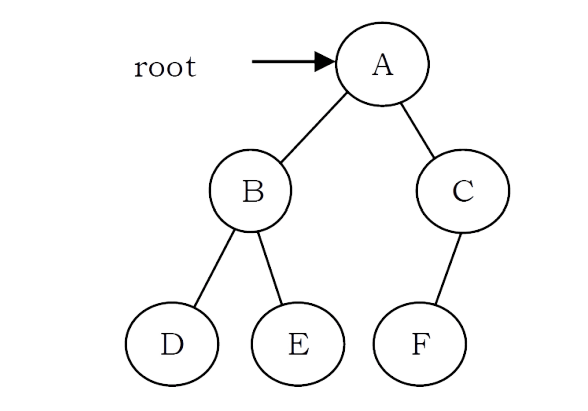
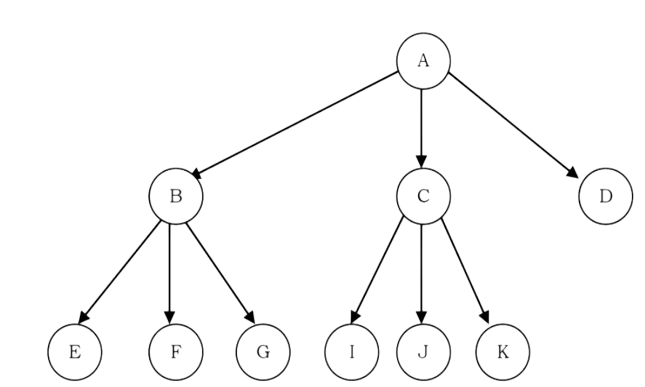
• The root of a tree is the node with no parents. There can be at most one root node in a tree (node A in the above example)
. • An edge refers to the link from parent to child (all links in the figure).
• A node with no children is called leaf node (E,J,K,H and I).
• Children of same parent are called siblings (B,C,D are siblings of A, and E,F are the siblings of B).
• A node p is an ancestor of node q if there exists a path from root to q and p appears on the path. The node q is called a descendant of p. For example, A,C and G are the ancestors of if.
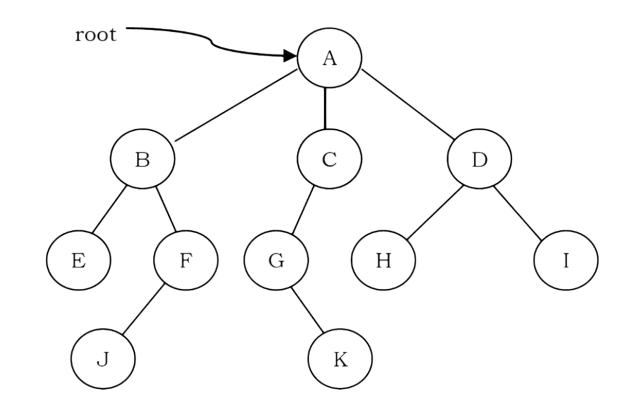
• The set of all nodes at a given depth is called the level of the tree (B, C and D are the same level). The root node is at level zero.
• The depth of a node is the length of the path from the root to the node (depth of G is 2, A – C – G).
• The height of a node is the length of the path from that node to the deepest node. The height of a tree is the length of the path from the root to the deepest node in the tree. A (rooted) tree with only one node (the root) has a height of zero. In the previous example, the height of B is 2 (B – F – J).
• Height of the tree is the maximum height among all the nodes in the tree and depth of the tree is the maximum depth among all the nodes in the tree. For a given tree, depth and height returns the same value. But for individual nodes we may get different results.
• The size of a node is the number of descendants it has including itself (the size of the subtree C is 3).
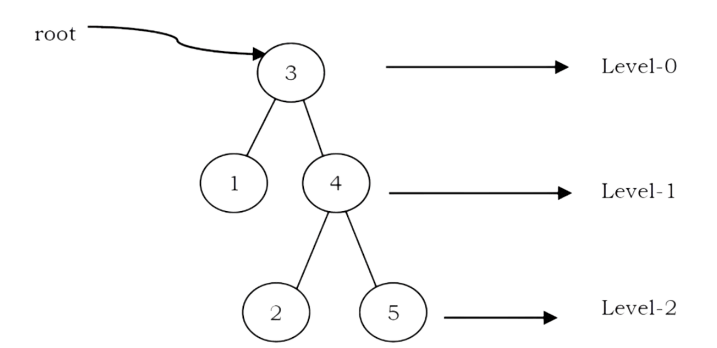
• If every node in a tree has only one child (except leaf nodes) then we call such trees skew trees. If every node has only left child then we call them left skew trees. Similarly, if every node has only right child then we call them right skew trees.
6.3 Binary Trees
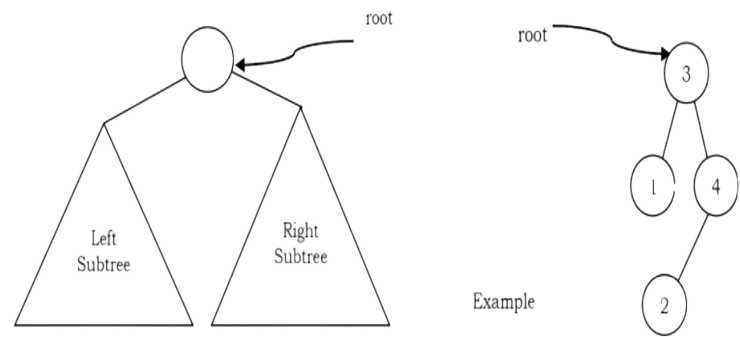
A tree is called binary tree if each node has zero child, one child or two children. Empty tree is also a valid binary tree. We can visualize a binary tree as consisting of a root and two disjoint binary trees, called the left and right subtrees of the root.
Generic Binary Tree
6.4 Types of Binary Trees
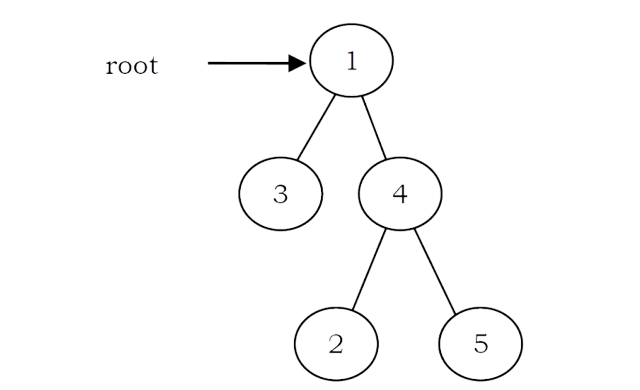
Strict Binary Tree: A binary tree is called strict binary tree if each node has exactly two children or no children.
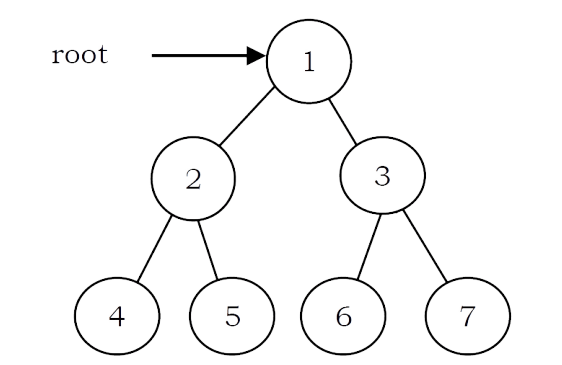
Full Binary Tree: A binary tree is called full binary tree if each node has exactly two children and all leaf nodes are at the same level.
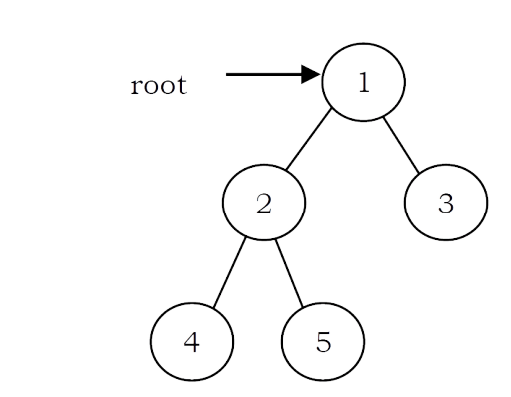
Complete Binary Tree: Before defining the complete binary tree, let us assume that the height of the binary tree is h. In complete binary trees, if we give numbering for the nodes by starting at the root (let us say the root node has 1) then we get a complete sequence from 1 to the number of nodes in the tree. While traversing we should give numbering for NULL pointers also. A binary tree is called complete binary tree if all leaf nodes are at height h or h – 1 and also without any missing number in the sequence.
6.5 Properties of Binary Trees
For the following properties, let us assume that the height of the tree is h. Also, assume that root node is at height zero.
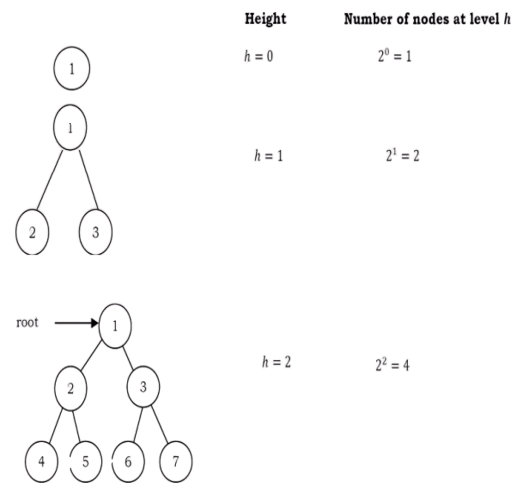
From the diagram we can infer the following properties:
• The number of nodes n in a full binary tree is 2 h+1 – 1. Since, there are h levels we need to add all nodes at each level [2 0 + 2 1+ 2 2 + ··· + 2 h = 2 h+1 – 1].
• The number of nodes n in a complete binary tree is between 2 h (minimum) and 2 h+1 – 1 (maximum). For more information on this, refer to Priority Queues chapter.
• The number of leaf nodes in a full binary tree is 2 h .
• The number of NULL links (wasted pointers) in a complete binary tree of n nodes is n + 1.
Structure of Binary Trees
Now let us define structure of the binary tree. For simplicity, assume that the data of the nodes are integers. One way to represent a node (which contains data) is to have two links which point to left and right children along with data fields as shown below:

struct Binary TreeNode{
int data;
struct BinaryTreeNode "left;
struct BinaryTreeNode "right;
}
Note: In trees, the default flow is from parent to children and it is not mandatory to show directed branches. For our discussion, we assume both the representations shown below are the same.

Operations on Binary Trees
Basic Operations
• Inserting an element into a tree
• Deleting an element from a tree
• Searching for an element
• Traversing the tree
Auxiliary Operations
• Finding the size of the tree
• Finding the height of the tree
• Finding the level which has maximum sum
• Finding the least common ancestor (LCA) for a given pair of nodes, and many more.
Applications of Binary Trees
Following are the some of the applications where binary trees play an important role:
• Expression trees are used in compilers.
• Huffman coding trees that are used in data compression algorithms.
• Binary Search Tree (BST), which supports search, insertion and deletion on a collection of items in O(logn) (average).
• Priority Queue (PQ), which supports search and deletion of minimum (or maximum) on a collection of items in logarithmic time (in worst case).
6.6 Binary Tree Traversals
In order to process trees, we need a mechanism for traversing them, and that forms the subject of this section. The process of visiting all nodes of a tree is called tree traversal. Each node is processed only once but it may be visited more than once. As we have already seen in linear data structures (like linked lists, stacks, queues, etc.), the elements are visited in sequential order. But, in tree structures there are many different ways.
Tree traversal is like searching the tree, except that in traversal the goal is to move through the tree in a particular order. In addition, all nodes are processed in the traversal but searching stops when the required node is found.
Traversal Possibilities
Starting at the root of a binary tree, there are three main steps that can be performed and the order in which they are performed defines the traversal type. These steps are: performing an action on the current node (referred to as “visiting” the node and denoted with “D”), traversing to the left child node (denoted with “L”), and traversing to the right child node (denoted with “R”). This process can be easily described through recursion. Based on the above definition there are 6 possibilities:
1. LDR: Process left subtree, process the current node data and then process right subtree
2. LRD: Process left subtree, process right subtree and then process the current node data
3. DLR: Process the current node data, process left subtree and then process right subtree
4. DRL: Process the current node data, process right subtree and then process left subtree
5. RDL: Process right subtree, process the current node data and then process left subtree
6. RLD: Process right subtree, process left subtree and then process the current node data
Classifying the Traversals
The sequence in which these entities (nodes) are processed defines a particular traversal method. The classification is based on the order in which current node is processed. That means, if we are classifying based on current node (D) and if D comes in the middle then it does not matter whether L is on left side of D or R is on left side of D
Similarly, it does not matter whether L is on right side of D or R is on right side of D. Due to this, the total 6 possibilities are reduced to 3 and these are:
• Preorder (DLR) Traversal
• Inorder (LDR) Traversal
• Postorder (LRD) Traversal
There is another traversal method which does not depend on the above orders and it is:
• Level Order Traversal: This method is inspired from Breadth First Traversal (BFS of Graph algorithms).
Let us use the diagram below for the remaining discussion.
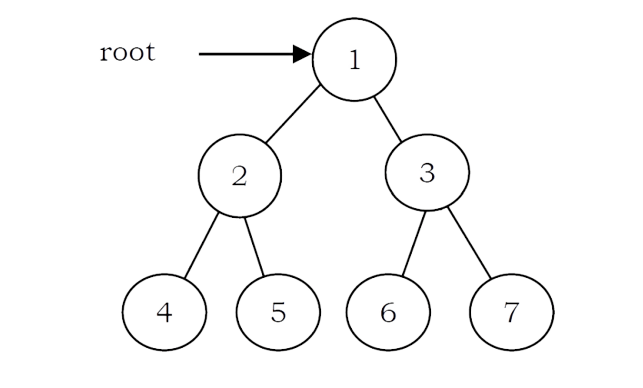
PreOrder Traversal
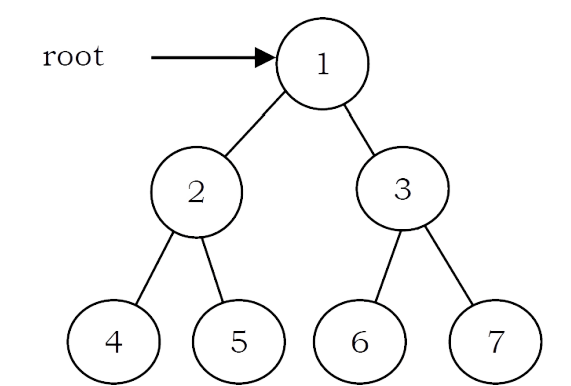
In preorder traversal, each node is processed before (pre) either of its subtrees. This is the simplest traversal to understand. However, even though each node is processed before the subtrees, it still requires that some information must be maintained while moving down the tree. In the example above, 1 is processed first, then the left subtree, and this is followed by the right subtree.
Therefore, processing must return to the right subtree after finishing the processing of the left subtree. To move to the right subtree after processing the left subtree, we must maintain the root information. The obvious ADT for such information is a stack. Because of its LIFO structure, it is possible to get the information about the right subtrees back in the reverse order.
Preorder traversal is defined as follows:
• Visit the root.
• Traverse the left subtree in Preorder.
• Traverse the right subtree in Preorder. The nodes of tree would be visited in the order: 1 2 4 5 3 6 7
void PreOrder(struct BinaryTreeNode *root){
if(root) {
printf("%d", root-data);
PreOrder(root-left);
PreOrder (root-right);
}
Time Complexity: O(n). Space Complexity: O(n).
Non-Recursive Preorder Traversal
In the recursive version, a stack is required as we need to remember the current node so that after completing the left subtree we can go to the right subtree. To simulate the same, first we process the current node and before going to the left subtree, we store the current node on stack. After completing the left subtree processing, pop the element and go to its right subtree. Continue this process until stack is nonempty
void PreOrderNonRecursive(struct BinaryTreeNode *root){ struct Stack *S = CreateStack();
}
while(1){
}
while(root) {
//Process current node
printf("%d", root-data);
Push(S,root);
//If left subtree exists, add to stack
root = root-left;
if(IsEmptyStack(S)) break;
root = Pop(S);
//Indicates completion of left subtree and current node, now go to right subtree
root = root-right;
DeleteStack(S);
Time Complexity: O(n). Space Complexity: O(n).
InOrder Traversal
In Inorder Traversal the root is visited between the subtrees. Inorder traversal is defined as follows:
• Traverse the left subtree in Inorder.
• Visit the root.
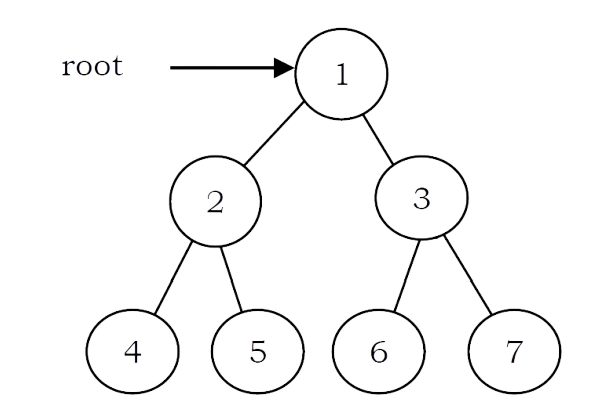
• Traverse the right subtree in Inorder. The nodes of tree would be visited in the order: 4 2 5 1 6 3 7
void InOrder(struct BinaryTreeNode *root){
if(root){
InOrder(root-left);
printf("%d",root-data);
InOrder(root-right);
Time Complexity: O(n). Space Complexity: O(n).
Non-Recursive Inorder Traversal
The Non-recursive version of Inorder traversal is similar to Preorder. The only change is, instead of processing the node before going to left subtree, process it after popping (which is indicated after completion of left subtree processing).
void InOrder Non Recursive(struct BinaryTreeNode *root){ struct Stack *S= CreateStack();
while(1){
while(root) {
}
Push(S,root);
//Got left subtree and keep on adding to stack root root-left;
if(IsEmptyStack(S))
break;
root = Pop(S);
printf("%d", root-data); //After popping, process the current node
//Indicates completion of left subtree and current node, now go to right subtree
root = root right;
DeleteStack(S);
Time Complexity: O(n). Space Complexity: O(n).
PostOrder Traversal
In postorder traversal, the root is visited after both subtrees. Postorder traversal is defined asfollows:
• Traverse the left subtree in Postorder.
• Traverse the right subtree in Postorder.
• Visit the root.
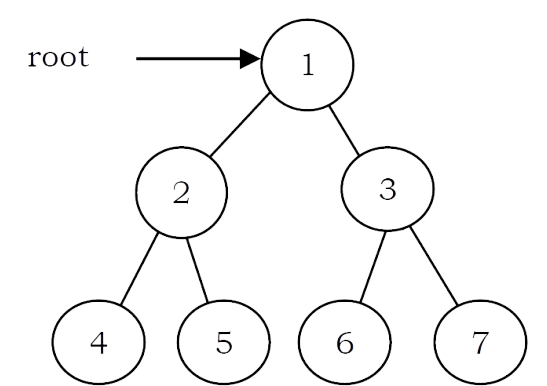
The nodes of the tree would be visited in the order: 4 5 2 6 7 3 1
void PostOrder(struct BinaryTreeNode *root){
if(root)
PostOrder(root-left);
PostOrder(root-right);
printf("%d", root-data);
Time Complexity: O(n). Space Complexity: O(n)
Non-Recursive Postorder
Traversal In preorder and inorder traversals, after popping the stack element we do not need to visit the same vertex again. But in postorder traversal, each node is visited twice. That means, after processing the left subtree we will visit the current node and after processing the right subtree we will visit the same current node. But we should be processing the node during the second visit. Here the problem is how to differentiate whether we are returning from the left subtree or the right subtree.
We use a previous variable to keep track of the earlier traversed node. Let’s assume current is the current node that is on top of the stack. When previous is current’s parent, we are traversing down the tree. In this case, we try to traverse to current’s left child if available (i.e., push left child to the stack). If it is not available, we look at current’s right child. If both left and right child do not exist (ie, current is a leaf node), we print current’s value and pop it off the stack.
If prev is current’s left child, we are traversing up the tree from the left. We look at current’s right child. If it is available, then traverse down the right child (i.e., push right child to the stack); otherwise print current’s value and pop it off the stack. If previous is current’s right child, we are traversing up the tree from the right. In this case, we print current’s value and pop it off the stack.
void PostOrderNonRecursive(struct BinaryTreeNode *root) { struct SimpleArrayStack *S = CreateStack();
struct BinaryTreeNode *previous = NULL;
do
}
while (root!=NULL){
Push(S, root);
root = root->left;
while(root == NULL && !IsEmptyStack(S)){
root = Top(S);
}
if(root->right == NULL || root->right == previous){
else
printf("%d", root->data);
Pop(S);
previous = root;
root = NULL;
root = root->right;
}
while (!IsEmptyStack(S));
Time Complexity: O(n). Space Complexity: O(n)
Level Order Traversal
Level order traversal is defined as follows:
• Visit the root.
• While traversing level (, keep all the elements at level ( + 1 in queue.
• Go to the next level and visit all the nodes at that level.
• Repeat this until all levels are completed.
The nodes of the tree are visited in the order: 1 2 3 4 5 6 7
void LevelOrder(struct BinaryTreeNode *root){ struct Binary TreeNode *temp; struct Queue Q = CreateQueue();
}
if(!root)
return;
EnQueue(Q,root); while (!IsEmptyQueue(Q)) { temp = DeQueue(Q); //Process current node
printf("%d", temp-data);
if(temp-left)
EnQueue(Q, temp-left);
if(temp-right)
EnQueue(Q, temp-right);
DeleteQueue(Q);
Time Complexity: O(n). Space Complexity: O(n). Since, in the worst case, all the nodes on the entire last level could be in the queue simultaneously
Binary Trees: Problems & Solutions
Problem-1 Give an algorithm for finding maximum element in binary tree.
Solution: One simple way of solving this problem is: find the maximum element in left subtree, find the maximum element in right sub tree, compare them with root data and select the one which is giving the maximum value. This approach can be easily implemented with recursion.
int FindMax(struct BinaryTreeNode *root) { int root_val, left, right, max = INT_MIN; if(root !=NULL) { root_val = root-data;
}
left = FindMax(root-left);
right = FindMax(root-right);
// Find the largest of the three values.
if(left > right) max = left;
else max = right; if(root_val> max) max = root_val;
return max;
Time Complexity: O(n). Space Complexity: O(n).
Problem-2 Give an algorithm for finding the maximum element in binary tree without recursion.
Solution: Using level order traversal: just observe the element’s data while deleting.
int FindMaxUsingLevelOrder(struct BinaryTreeNode *root){
struct BinaryTreeNode *temp; int max = INT_MIN;
struct Queue *Q= CreateQueue();
EnQueue(Q,root);
while (!IsEmptyQueue(Q)) { temp = DeQueue(Q);
}
// largest of the three values
if(max < temp-data)
max = temp-data;
if(temp-left)
EnQueue (Q, temp-left);
if(temp-right)
EnQueue (Q, temp-right);
DeleteQueue(Q);
return max;
Time Complexity: O(n). Space Complexity: O(n).
Problem-3 Give an algorithm for searching an element in binary tree.
Solution: Given a binary tree, return true if a node with data is found in the tree. Recurse down the tree, choose the left or right branch by comparing data with each node’s data
int FindInBinaryTreeUsingRecursion(struct BinaryTreeNode *root, int data) { int temp;
// Base case == empty tree, in that case, the data is not found so return false if(root == NULL)
return 0;
else {
//see if found here
if(data == root-data) return 1;
else {
// otherwise recur down the correct subtree
temp = FindInBinaryTreeUsingRecursion (root-left, data) if(temp != 0)
return temp;
else return(FindInBinaryTreeUsingRecursion(root-right, data));
return 0;
Time Complexity: O(n). Space Complexity: O(n).
Problem-4 Give an algorithm for searching an element in binary tree without recursion.
Solution: We can use level order traversal for solving this problem. The only change required in level order traversal is, instead of printing the data, we just need to check whether the root data is equal to the element we want to search.
int Search UsingLevelOrder(struct BinaryTreeNode *root, int data){
struct BinaryTreeNode *temp;
struct Queue *Q;
if(!root) return -1;
Q = CreateQueue(); EnQueue(Q,root);
while (!IsEmptyQueue(Q)) {
temp = DeQueue(Q);
//see if found here
if(data == root-data)
return 1;
if(temp-left)
EnQueue (Q, temp-left);
if(temp-right)
EnQueue (Q, temp-right);
}
DeleteQueue(Q);
return 0;
Time Complexity: O(n). Space Complexity: O(n).
Problem-5 Give an algorithm for inserting an element into binary tree.
Solution: Since the given tree is a binary tree, we can insert the element wherever we want. To insert an element, we can use the level order traversal and insert the element wherever we find the node whose left or right child is NULL.
void InsertInBinaryTree (struct BinaryTreeNode *root, int data){
struct Queue *Q;
struct BinaryTreeNode *temp;
struct BinaryTreeNode *newNode;
newNode = (struct BinaryTreeNode *) malloc(sizeof(struct BinaryTreeNode));
newNode-left = newNode-right = NULL;
if(!newNode) {
printf("Memory Error"); return;
if(!root){
}
root = newNode;
return;
Q = CreateQueue(); EnQueue(Q,root);
while (!IsEmptyQueue(Q)) { temp DeQueue(Q); if(temp-left)
else {
EnQueue(Q, temp-left);
temp-left-newNode; DeleteQueue(Q);
return;
if(temp-right)
EnQueue(0, temp-right):
else{
temp-right-newNode; DeleteQueue(Q);
return;
DeleteQueue(Q);
Time Complexity: O(n). Space Complexity: O(n).
Problem-6 Give an algorithm for finding the size of binary tree.
Solution: Calculate the size of left and right subtrees recursively, add 1 (current node) and return to its parent.
// Compute the number of nodes in a tree.
int SizeOfBinaryTree(struct BinaryTreeNode *root) {
if(root == NULL)
return 0;
else return(SizeOfBinaryTree(root-left) + 1 + SizeOfBinaryTree(root->right));
Time Complexity: O(n). Space Complexity: O(n).
Problem-7 Can we solve Problem-6 without recursion?
Solution: Yes, using level order traversal.
int SizeofBTUsingLevelOrder(struct BinaryTreeNode *root){
struct BinaryTreeNode *temp;
struct Queue *Q;
int count = 0;
if(!root) return 0;
Q = CreateQueue(); EnQueue(Q,root); while (!IsEmptyQueue(Q)) temp = DeQueue(Q);
count++;
if(temp-left)
EnQueue (Q, temp-left);
if(temp-right)
EnQueue (Q, temp-right);
}
DeleteQueue(Q);
return count;
Time Complexity: O(n). Space Complexity: O(n
Problem-8 Give an algorithm for printing the level order data in reverse order. For example, the output for the below tree should be: 4 5 6 7 2 3 1

void LevelOrderTraversalln Reverse(struct BinaryTreeNode *root){
struct Queue *Q;
struct Stack *s = CreateStack(); struct BinaryTreeNode *temp; if(!root) return;
Q = CreateQueue(); EnQueue(Q, root); while (!IsEmptyQueue(Q)) { temp = DeQueue(Q); if(temp-right)
EnQueue(Q, temp-right);
if(temp-left)
EnQueue (Q, temp-left);
Push(s, temp);
}
while (!IsEmptyStack(s))
printf("%d", Pop(s)-data);
Time Complexity: O(n). Space Complexity: O(n)
Problem-9 Give an algorithm for deleting the tree.
Solution:
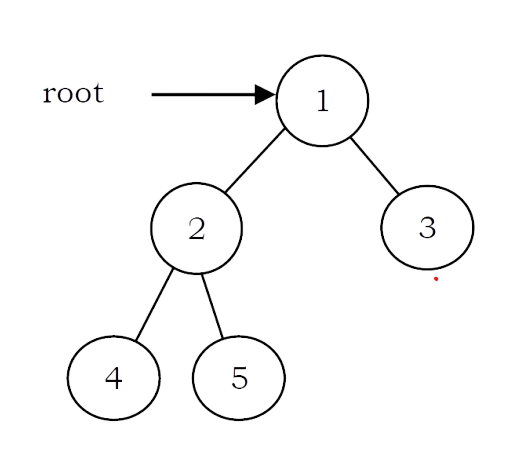
To delete a tree, we must traverse all the nodes of the tree and delete them one by one. So which traversal should we use: Inorder, Preorder, Postorder or Level order Traversal?
Before deleting the parent node we should delete its children nodes first. We can use postorder traversal as it does the work without storing anything. We can delete tree with other traversals also with extra space complexity. For the following, tree nodes are deleted in order – 4,5,2,3,1
void Delete BinaryTree(struct BinaryTreeNode *root){ if(root == NULL) return;
/* first delete both subtrees
Delete Binary Tree(root-left); DeleteBinaryTree(root-right);
//Delete current node only after deleting subtrees free(root);
Time Complexity: O(n). Space Complexity: O(n)
Problem-10 Give an algorithm for finding the height (or depth) of the binary tree.
Solution: Recursively calculate height of left and right subtrees of a node and assign height to the node as max of the heights of two children plus 1. This is similar to PreOrder tree traversal (and DFS of Graph algorithms).
int HeightOfBinaryTree(struct BinaryTreeNode *root){ int leftheight, rightheight;
if(root == NULL)
else{
return 0;
/* compute the depth of each subtree */ leftheight = HeightOfBinaryTree(root-left);
rightheight = HeightOfBinaryTree(root-right);
if(leftheight > rightheight)
return(leftheight + 1);
else
return(rightheight + 1);
Time Complexity: O(n). Space Complexity: O(n).
Problem-11 Can we solve Problem-10 without recursion?
Solution: Yes, using level order traversal. This is similar to BFS of Graph algorithms. End of level is identified with NULL.
void ReverseStack(struct Stack *S){ int data;
}
if(IsEmptyStack(S)) return;
data = Pop(S); ReverseStack(S); InsertAtBottom(S, data);
void InsertAtBottom(struct Stack *S, int data){
int temp; if(IsEmptyStack(S)) { Push(S, data);
}
return;
temp = Pop(S);
InsertAtBottom(S, data); Push(S, temp);
Time Complexity: O(n). Space Complexity: O(n).
Problem-12 Give an algorithm for finding the deepest node of the binary tree.
Solution:
struct Binary TreeNode *DeepestNodeinBinaryTree(struct BinaryTreeNode *root){
struct BinaryTreeNode *temp;
struct Queue *Q;
if(!root) return NULL;
Q = CreateQueue(); EnQueue(Q,root);
while (!IsEmptyQueue(Q)) { temp = DeQueue(Q);
}
if(temp-left)
EnQueue(Q, temp-left);
if(temp-right)
EnQueue(Q, temp-right);
DeleteQueue(Q);
return temp;
Time Complexity: O(n). Space Complexity: O(n).
Problem-13 Give an algorithm for deleting an element (assuming data is given) from binary tree.
Solution: The deletion of a node in binary tree can be implemented as
• Starting at root, find the node which we want to delete.
• Find the deepest node in the tree.
• Replace the deepest node’s data with node to be deleted.
• Then delete the deepest node.
Problem-14 Give an algorithm for finding the number of leaves in the binary tree without using recursion.
Solution: The set of nodes whose both left and right children are NULLare called leaf nodes
int NumberOfLeaves InBTusingLevelOrder(struct BinaryTreeNode *root){
struct BinaryTreeNode *temp;
struct Queue *Q;
int count = 0;
if(!root) return 0; Q = CreateQueue(); EnQueue(Q,root); while (!IsEmptyQueue(Q)) { temp = DeQueue(Q);
if(!temp-left && !temp-right) count++;
else{ if(temp-left)
DeleteQueue(Q);
return count;
EnQueue(Q, temp-left);
if(temp-right)
EnQueue(Q, temp-right);
Time Complexity: O(n). Space Complexity: O(n)
Problem-15 Give an algorithm for finding the number of full nodes in the binary tree without using recursion.
Solution: The set of all nodes with both left and right children are called full nodes.
int NumberOfFullNodesInBTusingLevelOrder(struct BinaryTreeNode *root){
struct BinaryTreeNode *temp;
struct Queue *Q;
int count = 0;
if(!root)
return 0;
Q = CreateQueue(); EnQueue(Q,root); while (!IsEmptyQueue(Q)) { temp = DeQueue(Q); if(temp-left && temp-right) count++;
if(temp-left)
}
EnQueue (Q, temp-left);
if(temp-right)
EnQueue (Q, temp-right);
DeleteQueue(Q);
return count;
Time Complexity: O(n). Space Complexity: O(n)
Problem-16 Give an algorithm for finding the number of half nodes (nodes with only one child) in the binary tree without using recursion.
Solution: The set of all nodes with either left or right child (but not both) are called half nodes.
int NumberOfHalf NodesInBTusingLevelOrder(struct BinaryTreeNode *root){
struct BinaryTreeNode *temp;
struct Queue *Q;
int count = 0; if(!root) return 0; Q = CreateQueue(); EnQueue(Q,root);
while (!IsEmptyQueue(Q)) { temp = DeQueue(Q);
//we can use this condition also instead of two temp-left ^ temp-right if(!temp-left && temp-right || temp-left && !temp->right)
count++;
if(temp-left)
EnQueue (Q, temp-left);
if(temp-right)
EnQueue (Q, temp-right);
DeleteQueue(Q);
return count;
Time Complexity: O(n). Space Complexity: O(n)
Problem-17 Given two binary trees, return true if they are structurally identical.
Solution:
Algorithm:
• If both trees are NULLthen return true.
• If both trees are not NULL, then compare data and recursively check left and right subtree structures.
//Return true if they are structurally identical.
int AreStructurullySame Trees (struct BinaryTreeNode *root1, struct BinaryTreeNode *root2) { // both empty→1
if(root1==NULL && root2==NULL) return 1;
if(root1==NULL || root2==NULL) return 0;
// both non-empty-compare them
return(root1-data == root2-data && AreStructurullySameTrees(root1-left, root2-left) && AreStructurully SameTrees(root1-right, root2-right));
Time Complexity: O(n). Space Complexity: O(n), for recursive stack.
Problem-18 Give an algorithm for finding the diameter of the binary tree. The diameter of a tree (sometimes called the width) is the number of nodes on the longest path between two leaves in the tree.
Solution: To find the diameter of a tree, first calculate the diameter of left subtree and right subtrees recursively. Among these two values, we need to send maximum value along with current level (+1).
int DiameterOfTree(struct BinaryTreeNode *root, int *ptr){
}
}
int left, right; if(!root)
return 0;
left DiameterOfTree(root-left, ptr);
=
right DiameterOfTree(root-right, ptr);
if(left + right > *ptr)
*ptr = left + right;
return Max(left, right)+1;
//Alternative Coding
static int diameter(struct BinaryTreeNode *root) {
if (root == NULL) return 0;
int IHeight = height(root->eft); int rHeight = height(root-right);
int IDiameter diameter(root-left);
=
int rDiameter diameter(root-right);
return max(Height+rHeight + 1, max(IDiameter, rDiameter));
/* The function Compute the "height" of a tree. Height is the number of nodes along the longest path from the root node down to the farthest leaf node.*/
static int height(Node root) {
if (root == null) return 0;
return 1+ max(height(root.left), height(root.right));
There is another solution and the complexity is O(n). The main idea of this approach is that the node stores its left child’s and right child’s maximum diameter if the node’s child is the “root”, therefore, there is no need to recursively call the height method. The drawback is we need to add two extra variables in the node structure.
int findMaxLen(Node root) { int nMaxLen = 0; if (root == null) return 0;
if (root.left == null) root.nMaxLeft = 0;
}
if (root.right == null) root.nMaxRight = 0;
if (root.left!= null)
findMaxLen(root.left);
if (root.right != null)
findMaxLen(root.right);
if (root.left!= null) {
int nTempMaxLen = 0;
nTempMaxLen = (root.left.nMaxLeft > root.left.nMaxRight)? root.left.nMaxLeft: root.left.nMaxRight;
root.nMaxLeftnTempMaxLen + 1;
if (root.right != null) {
int nTempMaxLen = 0;
nTempMaxLen = (root.right.nMaxLeft > root.right.nMaxRight)?
root.right.nMaxLeft: root.right.nMaxRight;
root.nMaxRight nTempMaxLen + 1;
if (root.nMaxLeft+ root.nMaxRight > nMaxLen) nMaxLen = root.nMaxLeft + root.nMaxRight;
return nMaxLen;
Time Complexity: O(n). Space Complexity: O(n)
Problem-19 Give an algorithm for finding the level that has the maximum sum in the binary tree.
Solution: The logic is very much similar to finding the number of levels. The only change is, we n e e d t o ke e p tr a c k o f th e s ums a s w e l l
int FindLevelwithMaxSum(struct BinaryTreeNode *root){ struct BinaryTreeNode *temp;
int level=0, maxLevel=0;
struct Queue *Q;
int currentSum= 0, maxSum = 0;
if(!root)
return 0;
Q-CreateQueue();
EnQueue(Q,root);
EnQueue(Q,NULL);
while (!IsEmptyQueue(Q)){
temp -DeQueue(Q);
//End of first level.
// If the current level is completed then compare sums
if(temp == NULL) {
if(currentSum> maxSum) {
}
maxSum = currentSum;
maxLevel = level;
currentSum = 0;
//place the indicator for end of next level at the end of queue
if(!IsEmptyQueue(Q))
EnQueue(Q,NULL);
level++;
}
else {
currentSum += temp-data;
if(temp-left)
EnQueue(temp, temp-left);
if(root-right)
EnQueue(temp, temp-right);
}
return maxLevel;
Time Complexity: O(n). Space Complexity: O(n).
Problem-20 Given a binary tree, print out all its root-to-leaf paths.
Solution: Refer to comments in functions.
void PrintPaths Recur(struct BinaryTreeNode *root, int path[], int pathLen) { if(root == NULL) return;
// append this node to the path array path[pathLen] root-data; pathLen++;
// it's a leaf, so print the path that led to here
if(root-left==NULL && root-right ==NULL) PrintArray(path, pathLen);
else{
// otherwise try both subtrees
PrintPaths Recur(root-left, path, pathLen); PrintPaths Recur(root-right, path, pathLen);
// Function that prints out an array on a line. void PrintArray(int ints[], int len) {
for (int i=0; i<len; i++)
printf("%d",ints[i]);
Time Complexity: O(n). Space Complexity: O(n), for recursive stackTime Complexity: O(n). Space Complexity: O(n), for recursive stack
Problem-21 Give an algorithm for checking the existence of path with given sum. That means, given a sum, check whether there exists a path from root to any of the nodes.
Solution: For this problem, the strategy is: subtract the node value from the sum before calling its children recursively, and check to see if the sum is 0 when we run out of tree.
void PrintPaths Recur(struct BinaryTreeNode *root, int path[], int pathLen) { if(root ==NULL) return;
// append this node to the path array path[pathLen] root-data; pathLen++;
// it's a leaf, so print the path that led to here
if(root-left-NULL && root-right == NULL) PrintArray(path, pathLen);
else{
// otherwise try both subtrees
PrintPaths Recur(root-left, path, pathLen); PrintPaths Recur(root-right, path, pathLen);
// Function that prints out an array on a line. void PrintArray(int ints[], int len) { for (int i=0; i<len; i++)
printf("%d",ints[i]);
if((root-left && root-right) | | (!root-left && !root-right)) return(HasPathSum(root-left, remainingSum) || HasPathSum(root-right, remainingSum));
else if(root-left)
else
return HasPathSum(root-left, remainingSum);
return HasPathSum(root-right, remainingSum);
Time Complexity: O(n). Space Complexity: O(n).
Problem-22 Give an algorithm for finding the sum of all elements in binary tree.
Solution: Recursively, call left subtree sum, right subtree sum and add their values to current nodes data.
int Add(struct BinaryTreeNode *root) {
if(root == NULL) return 0;
else return (root-data+Add(root-left)+ Add(root-right));
Time Complexity: O(n). Space Complexity: O(n).
Problem-23 Can we solve Problem-22 without recursion?
Solution: We can use level order traversal with simple change. Every time after deleting an element from queue, add the nodes data value to sum variable.
int SumofBTusingLevelOrder(struct BinaryTreeNode *root){ struct BinaryTreeNode *temp;
struct Queue *Q;
int sum = 0;
if(!root)
return 0;
Q = CreateQueue();
EnQueue(Q,root); while(!IsEmptyQueue(Q)) {
temp = DeQueue(Q);
sum += temp-data;
if(temp-left)
if(temp-right)
EnQueue (Q, temp-left);
EnQueue (Q, temp-right);
DeleteQueue(Q);
return sum;
Time Complexity: O(n). Space Complexity: O(n).
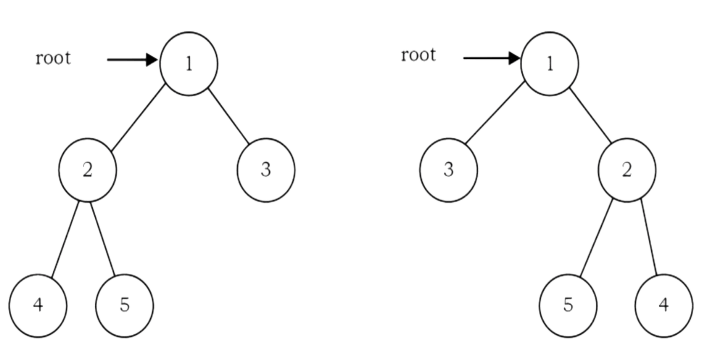
Problem-24 Give an algorithm for converting a tree to its mirror. Mirror of a tree is another tree with left and right children of all non-leaf nodes interchanged. The trees below are mirrors to each other.
struct BinaryTreeNode *MirrorOfBinaryTree(struct BinaryTreeNode *root){ struct BinaryTreeNode* temp;
if(root) {
MirrorOfBinaryTree(root-left); MirrorOfBinaryTree(root-right);
/* swap the pointers in this node */
temp-root-left;
root-left-root-right; root-right = temp;
}
return root;
Time Complexity: O(n). Space Complexity: O(n).
Problem-25 Given two trees, give an algorithm for checking whether they are mirrors of each other.
Solution
int AreMirrors(struct BinaryTreeNode root1, struct BinaryTreeNode * root2) {
if(root1 == NULL && root2 == NULL)
return 1;
if(root1 == NULL || root2 == NULL)
return 0;
if(root 1-data = root2→data)
return 0;
else return Are Mirrors(root1-left, root2-right) && AreMirrors (root 1-right, root2-left);
Problem-26 Give an algorithm for finding LCA (Least Common Ancestor) of two nodes in a Binary Tree.
Solution:
struct BinaryTreeNode *LCA(struct BinaryTreeNode *root, struct BinaryTreeNode *a, struct BinaryTreeNode *ẞ){
struct Binary TreeNode *left, *right;
if(root == NULL)
return root;
if(root
t == a || root == |
B)
return root;
left = LCA (root-left, a, ß);
=
right LCA (root right, a, ẞ);
if(left && right) return root;
else return (left? left: right)
Time Complexity: O(n). Space Complexity: O(n) for recursion
Problem-27 Give an algorithm for constructing binary tree from given Inorder and Preorder traversals.
Solution: Let us consider the traversals below:
Inorder sequence: D B E A F C
Preorder sequence: A B D E C F

In a Preorder sequence, leftmost element denotes the root of the tree. So we know ‘A’ is the root for given sequences. By searching ‘A’ in Inorder sequence we can find out all elements on the left side of ‘A’, which come under the left subtree, and elements on the right side of ‘A’, which come under the right subtree. So we get the structure as seen below.
We recursively follow the above steps and get the following tree
Algorithm: BuildTree()
1 Select an element from Preorder. Increment a Preorder index variable (preOrderIndex in code below) to pick next element in next recursive call.
2 Create a new tree node (newNode) from heap with the data as selected element.\
3 Find the selected element’s index in Inorder. Let the index be inOrderIndex.
4 Call BuildBinaryTree for elements before inOrderIndex and make the built tree as left subtree of newNode.
5 Call BuildBinaryTree for elements after inOrderIndex and make the built tree as right subtree of newNode.
6 return newNode.
struct BinaryTreeNode *BuildBinaryTree(int inOrder]], int preOrder[], int inOrderStart, int inOrderEnd){ static int preOrderIndex = 0;
}
struct BinaryTreeNode *newNode; if(inOrderStart > inOrderEnd) return NULL;
newNode = (struct BinaryTreeNode *) malloc (sizeof(struct BinaryTreeNode));
if(!newNode) {
printf("Memory Error");
return NULL;
Select current node from Preorder traversal using preOrderIndex
newNode-data preOrder[preOrderIndex];
preOrderIndex++;
if(inOrderStart == inOrderEnd)
return newNode;
// find the index of this node in Inorder traversal
int inOrderIndex Search(inOrder, inOrderStart, inOrderEnd, newNode-data); //Fill the left and right subtrees using index in Inorder traversal
newNode-left = BuildBinaryTree (inOrder, preOrder, inOrderStart, inOrderIndex -1); newNode-right = BuildBinaryTree (in Order, preOrder, inOrderIndex +1, inOrderEnd); return newNode;
Time Complexity: O(n). Space Complexity: O(n)
Problem-28 If we are given two traversal sequences, can we construct the binary tree uniquely?
Solution: It depends on what traversals are given. If one of the traversal methods is Inorder then the tree can be constructed uniquely, otherwise not.
Therefore, the following combinations can uniquely identify a tree:
• Inorder and Preorder
• Inorder and Postorder
• Inorder and Level-order
The following combinations do not uniquely identify a tree.
• Postorder and Preorder
• Preorder and Level-order
• Postorder and Level-order For example, Preorder, Level-order and Postorder traversals are the same for the above trees:

So, even if three of them (PreOrder, Level-Order and PostOrder) are given, the tree cannot be constructed uniquely.
Problem-29 Give an algorithm for printing all the ancestors of a node in a Binary tree. For the tree below, for 7 the ancestors are 1 3 7
Solution: Apart from the Depth First Search of this tree, we can use the following recursive way to print the ancestors
int PrintAllAncestors(struct BinaryTreeNode *root, struct BinaryTreeNode *node){ if(root == NULL) return 0;
if(root-left == node || root-right == node || PrintAllAncestors (root-left, node) || PrintAllAncestors (root-right, node)) {
printf("%d", root-data);
return 1;
return 0;
Time Complexity: O(n). Space Complexity: O(n) for recursion
Problem-30 Zigzag Tree Traversal: Give an algorithm to traverse a binary tree in Zigzag order. For example, the output for the tree below should be: 1 3 2 4 5 6 7
Solution: This problem can be solved easily using two stacks. Assume the two stacks are: currentLevel and nextLevel. We would also need a variable to keep track of the current level order (whether it is left to right or right to left).
We pop from currentLevel stack and print the node’s value. Whenever the current level order is from left to right, push the node’s left child, then its right child, to stack nextLevel. Since a stack is a Last In First Out (LIFO) structure, the next time that nodes are popped off nextLevel, it will be in the reverse order.
On the other hand, when the current level order is from right to left, we would push the node’s right child first, then its left child. Finally, don’t forget to swap those two stacks at the end of each level (i. e., when currentLevel is empty).
void ZigZag Traversal(struct BinaryTreeNode *root){ struct BinaryTreeNode *temp;
int leftToRight = 1;
if(root)
return;
struct Stack *currentLevel = CreateStack(), "nextLevel = CreateStack(); Push(currentLevel, root); while(!IsEmptyStack(currentLevel) { temp = Pop(currentLevel);
if(temp) {
}
printf("%d", temp-data);
if(leftToRight){
if(temp-left) Push(nextLevel, temp→left); if(temp-right) Push(nextLevel, temp→right);
else if(temp-right) Push(nextLevel, temp-right); if(temp-left) Push(nextLevel, temp-left);
if(IsEmptyStack(currentLevel]) {
leftToRight = 1-leftToRight;
swap(currentLevel, nextLevel);
Time Complexity: O(n). Space Complexity: Space for two stacks = O(n) + O(n) = O(n)
Problem-31 Give an algorithm for finding the vertical sum of a binary tree. For example, The tree has 5 vertical lines
Vertical-1: nodes-4 => vertical sum is 4
Vertical-2: nodes-2 => vertical sum is 2
Vertical-3: nodes-1,5,6 => vertical sum is 1 + 5 + 6 = 12
Vertical-4: nodes-3 => vertical sum is 3
Vertical-5: nodes-7 => vertical sum is 7 We need to output: 4 2 12 3 7
Solution: We can do an inorder traversal and hash the column. We call VerticalSumlnBinaryTreefroot, 0) which means the root is at column 0. While doing the traversal, hash the column and increase its value by root → data.
void VerticalSumInBinaryTree (struct BinaryTreeNode *root, int column){ if(root == NULL) return;
VerticalSumInBinaryTree(root-left, column-1);
//Refer Hashing chapter for implementation of hash table Hash[column] += root-data;
VerticalSumInBinaryTree(root-right, column+1);
VerticalSumInBinaryTree(root, 0);
Print Hash;
Problem-32 How many different binary trees are possible with n nodes?
Solution: For example, consider a tree with 3 nodes (n = 3). It will have the maximum combination of 5 different (i.e., 2 3 -3 = 5) trees
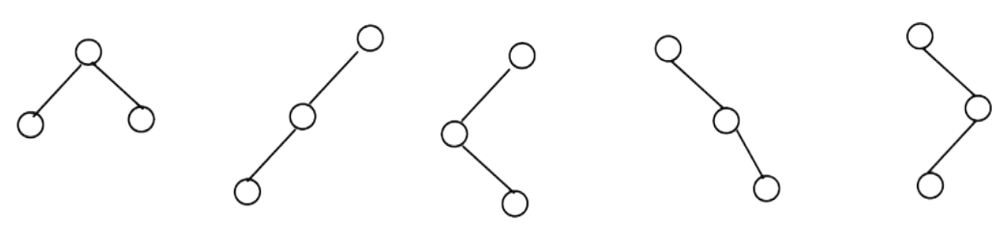
In general, if there are n nodes, there exist 2 n –n different trees.
Problem-33 Given a tree with a special property where leaves are represented with ‘L’ and internal node with ‘I’. Also, assume that each node has either 0 or 2 children. Given preorder traversal of this tree, construct the tree.
Example: Given preorder string => ILILL
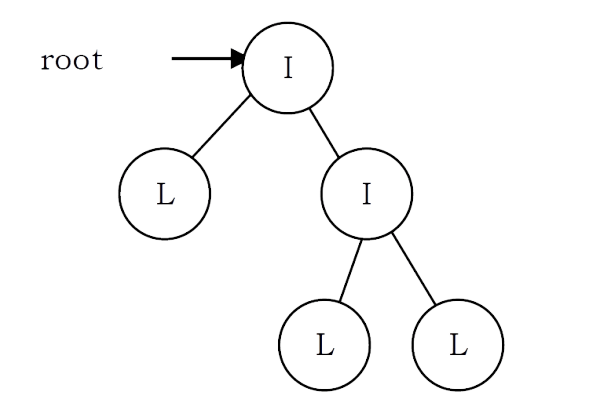
Solution: First, we should see how preorder traversal is arranged. Pre-order traversal means first put root node, then pre-order traversal of left subtree and then pre-order traversal of right subtree. In a normal scenario, it’s not possible to detect where left subtree ends and right subtree starts using only pre-order traversal. Since every node has either 2 children or no child, we can surely say that if a node exists then its sibling also exists. So every time when we are computing a subtree, we need to compute its sibling subtree as well.
Secondly, whenever we get ‘L’ in the input string, that is a leaf and we can stop for a particular subtree at that point. After this ‘L’ node (left child of its parent ‘L’), its sibling starts. If ‘L’ node is right child of its parent, then we need to go up in the hierarchy to find the next subtree to compute.
Keeping the above invariant in mind, we can easily determine when a subtree ends and the next one starts. It means that we can give any start node to our method and it can easily complete the subtree it generates going outside of its nodes. We just need to take care of passing the correct start nodes to different sub-trees.
struct BinaryTreeNode *BuildTreeFromPreOrder(char* A, int *i){ struct BinaryTreeNode *newNode;
newNode = (struct BinaryTreeNode *) malloc(sizeof(struct BinaryTreeNode));
newNode->data =A[i];
newNode-left = newNode-right = NULL;
if(A == NULL){
free(newNode);
return NULL;
//Boundary Condition
}
if(A[i]=='L)
//On reaching leaf node, return
return newNode;
*-*+1;
//Populate left sub tree
=
*=i+1;
newNode-left BuildTree FromPreOrder(A, i);
newNode-right = BuildTree From PreOrder(A, i);
return newNode;
//Populate right sub tree
Time Complexity: O(n)
Problem-34 Given a binary tree with three pointers (left, right and nextSibling), give an algorithm for filling the nextSibling pointers assuming they are NULLinitially.
Solution: We can use simple queue (similar to the solution of Problem-11). Let us assume that the structure of binary tree is:
struct BinaryTreeNode{ struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
struct BinaryTreeNode* nextSibling;
int Fill NextSiblings(struct BinaryTreeNode *root){ struct BinaryTreeNode "temp;
struct Queue *Q;
if(root)
return 0;
Q = CreateQueue(); EnQueue(Q,root); EnQueue(Q,NULL);
while (!IsEmptyQueue(Q)){ temp =DeQueue(Q);
// Completion of current level.
if(temp = NULL) { //Put another marker for next level. if(!IsEmptyQueue(Q))
EnQueue(Q,NULL);
}
else
{
temp-nextSibling = QueueFront(Q);
if(root-left)
EnQueue(Q, temp-left);
if(root-right)
EnQueue(Q, temp-right);
Time Complexity: O(n). Space Complexity: O(n).
Problem-35 Is there any other way of solving Problem-34?
Solution: The trick is to re-use the populated nextSibling pointers. As mentioned earlier, we just need one more step for it to work. Before we pass the left and right to the recursion function itself, we connect the right child’s nextSibling to the current node’s nextSibling left child. In order for this to work, the current node nextSibling pointer must be populated, which is true in this case.
void Fill NextSiblings(struct BinaryTreeNode* root) {
if (!root) return;
if (root-left)
root-left-nextSibling = root-right;
if (root-right)
root-right-nextSibling = (root-nextSibling) ? root-nextSibling-left: NULL;
Fill NextSiblings(root-left);
Fill NextSiblings(root-right);
}
Time Complexity: O(n).
6.7 Generic Trees (N-ary Trees)
In the previous section we discussed binary trees where each node can have a maximum of two children and these are represented easily with two pointers. But suppose if we have a tree with many children at every node and also if we do not know how many children a node can have, how do we represent them?
For example, consider the tree shown below.
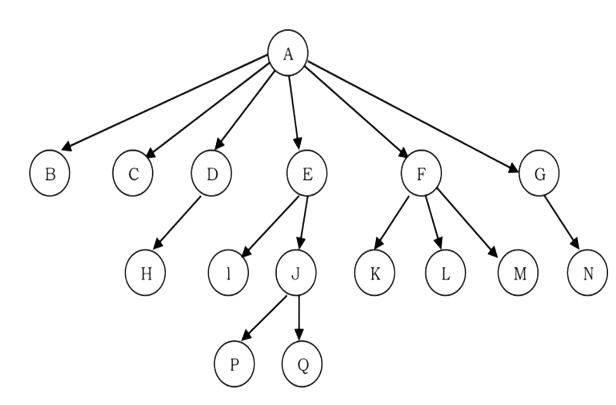
How do we represent the tree? In the above tree, there are nodes with 6 children, with 3 children, with 2 children, with 1 child, and with zero children (leaves). To present this tree we have to consider the worst case (6 children) and allocate that many child pointers for each node. Based on this, the node representation can be given as:
struct TreeNode int data;
struct TreeNode *firstChild;
struct TreeNode *secondChild;
struct TreeNode *thirdChild;
struct TreeNode "fourth Child;
struct TreeNode "fifth Child;
struct TreeNode *sixth Child;
Since we are not using all the pointers in all the cases, there is a lot of memory wastage. Another problem is that we do not know the number of children for each node in advance. In order to solve this problem we need a representation that minimizes the wastage and also accepts nodes with any number of children.
Representation of Generic Trees
Since our objective is to reach all nodes of the tree, a possible solution to this is as follows:
• At each node link children of same parent (siblings) from left to right.
• Remove the links from parent to all children except the first child.
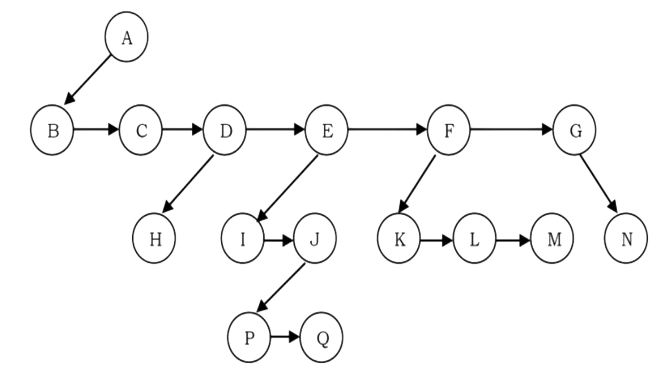
What these above statements say is if we have a link between children then we do not need extra links from parent to all children. This is because we can traverse all the elements by starting at the first child of the parent. So if we have a link between parent and first child and also links between all children of same parent then it solves our problem.
This representation is sometimes called first child/next sibling representation. First child/next sibling representation of the generic tree is shown above. The actual representation for this tree is:
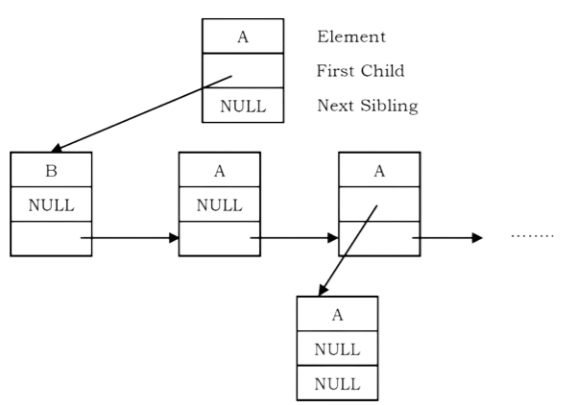
Based on this discussion, the tree node declaration for general tree can be given as:
struct TreeNode{ int data;
struct TreeNode *firstChild; struct TreeNode "nextSibling;
Note: Since we are able to convert any generic tree to binary representation; in practice we use
binary trees. We can treat all generic trees with a first child/next sibling representation as binary
trees.
Generic Trees: Problems & Solutions
Problem-36 Given a tree, give an algorithm for finding the sum of all the elements of the tree.
Solution: The solution is similar to what we have done for simple binary trees. That means, traverse the complete list and keep on adding the values. We can either use level order traversal or simple recursion.
int FindSum(struct TreeNode *root){
if(!root) return 0;
return root-data + FindSum(root-firstChild) + FindSum(root-nextSibling);
Time Complexity: O(n). Space Complexity: O(1) (if we do not consider stack space), otherwise O(n).
Note: All problems which we have discussed for binary trees are applicable for generic trees also. Instead of left and right pointers we just need to use firstChild and nextSibling.
Problem-37 For a 4-ary tree (each node can contain maximum of 4 children), what is the maximum possible height with 100 nodes? Assume height of a single node is 0.
Solution: In 4-ary tree each node can contain 0 to 4 children, and to get maximum height, we need to keep only one child for each parent. With 100 nodes, the maximum possible height we can get is 99. If we have a restriction that at least one node has 4 children, then we keep one node with 4 children and the remaining nodes with 1 child. In this case, the maximum possible height is 96. Similarly, with n nodes the maximum possible height is n – 4.
Problem-38 For a 4-ary tree (each node can contain maximum of 4 children), what is the minimum possible height with n nodes?
Solution: Similar to the above discussion, if we want to get minimum height, then we need to fill all nodes with maximum children (in this case 4). Now let’s see the following table, which indicates the maximum number of nodes for a given height.


For a given height h the maximum possible nodes are:4h+1-1/3 . To get minimum height, take
logarithm on both sides
Problem-39 Given a parent array P, where P[i] indicates the parent of i th node in the tree (assume parent of root node is indicated with –1). Give an algorithm for finding the height or depth of the tree.
Solution:
For example: if the P is

Its corresponding tree is:
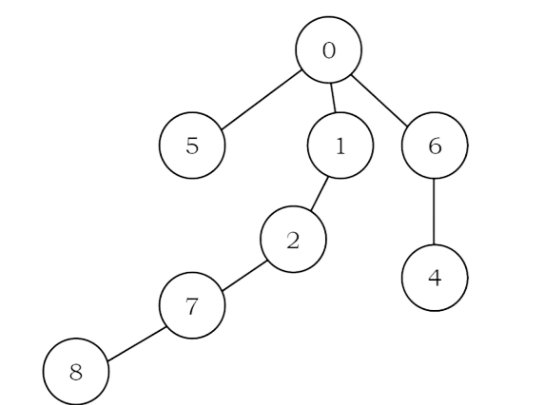
From the problem definition, the given array represents the parent array. That means, we need to consider the tree for that array and find the depth of the tree. The depth of this given tree is 4. If we carefully observe, we just need to start at every node and keep going to its parent until we reach –1 and also keep track of the maximum depth among all nodes.
int FindDepthInGenericTree(int P[], int n){ int maxDepth =-1, currentDepth =-1, j; for (int i=0; i < n; i++) {
currentDepth = 0; j = i;
while(Pj] != -1) {
currentDepth++; j = Plj];
}
if(currentDepth> maxDepth)
maxDepth = currentDepth;
}
return maxDepth;
Time Complexity: O(n 2 ). For skew trees we will be re-calculating the same values. Space Complexity: O(1).
Note: We can optimize the code by storing the previous calculated nodes’ depth in some hash table or other array. This reduces the time complexity but uses extra space.
Problem-40 Given a node in the generic tree, give an algorithm for counting the number of siblings for that node.
Solution: Since tree is represented with the first child/next sibling method, the tree structure can be given as:
struct TreeNode int data;
struct TreeNode *firstChild;
}
struct TreeNode *nextSibling;
For a given node in the tree, we just need to traverse all its next siblings
int SiblingsCount(struct TreeNode *current){ int count = 0;
while(current) { count++;
}
current = current-nextSibling;
reutrn count;
Time Complexity: O(n). Space Complexity: O(1).
Problem-41 Given a node in the generic tree, give an algorithm for counting the number of children for that node.
Solution: Since the tree is represented as first child/next sibling method, the tree structure can be given as:
struct TreeNode{ int data;
struct TreeNode *firstChild; struct TreeNode "nextSibling;
For a given node in the tree, we just need to point to its first child and keep traversing all its next siblings.
int ChildCount(struct TreeNode *current){ int count = 0;
current current-firstChild;
while(current) { count++;
current = current-nextSibling;
reutrn count;
Time Complexity: O(n). Space Complexity: O(1).
Problem-42 Given two trees how do we check whether the trees are isomorphic to each other or not?
Solution:
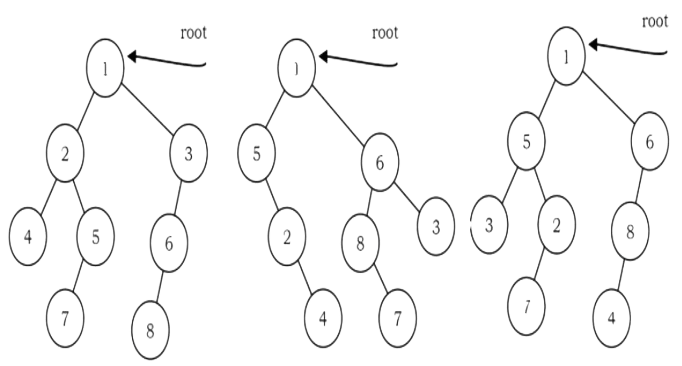
Two binary trees root1 and root2 are isomorphic if they have the same structure. The values of the nodes does not affect whether two trees are isomorphic or not. In the diagram below, the tree in the middle is not isomorphic to the other trees, but the tree on the right is isomorphic to the tree on the left.
int IsIsomorphic(struct TreeNode *root1, struct TreeNode *root2){
if(!root1 && !root2) return 1;
if(!root] && root2) || (root] && !root2))
return 0;
return (IsIsomorphic(root1-left, root2-left) && IsIsomorphic(root1-right, root2-right));
Time Complexity: O(n). Space Complexity: O(n).
Problem-43 Given two trees how do we check whether they are quasi-isomorphic to each other or not?
Solution:
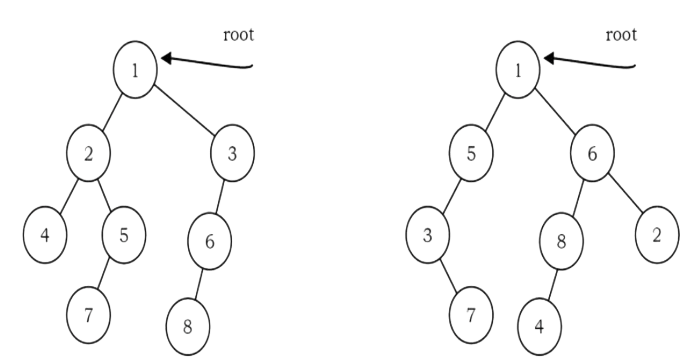
Two trees root1 and root2 are quasi-isomorphic if root1 can be transformed into root2 by
swapping the left and right children of some of the nodes of root1. Data in the nodes are not
important in determining quasi-isomorphism; only the shape is important. The trees below are
quasi-isomorphic because if the children of the nodes on the left are swapped, the tree on the right
is obtained.
int Quasilsomorphic(struct TreeNode *root1, struct TreeNode *root2){
if(!root1 && !root2 return 1;
if(!root1 && root2) || (root1 && !root2))
return 0;
return (Quasilsomorphic(root1-left, root2-left) && Quasilsomorphic(root1-right, root2-right)
|| Quasilsomorphic(root1-right, root2-left) && Quasilsomorphic(root 1-left, root2-right));
Time Complexity: O(n). Space Complexity: O(n).
Problem-44 A full k –ary tree is a tree where each node has either 0 or k children. Given an array which contains the preorder traversal of full k –ary tree, give an algorithm for constructing the full k –ary tree.
Solution: In k –ary tree, for a node at i th position its children will be at k * i + 1 to k * i + k. For example, the example below is for full 3-ary tree.
As we have seen, in preorder traversal first left subtree is processed then followed by root node and right subtree. Because of this, to construct a full k-ary, we just need to keep on creating the nodes without bothering about the previous constructed nodes. We can use this trick to build the tree recursively by using one global index. The declaration for k-ary tree can be given as:
struct K-aryTreeNode{ char data;
struct K-aryTreeNode "child[];
int *Ind = 0;
struct K-aryTreeNode *BuildK-aryTree(char A[], int n, int k){
if(n<=0) return NULL;
struct K-aryTreeNode *newNode = (struct K-aryTreeNode*) malloc(sizeof(struct K-aryTreeNode));
if(!newNode) {
printf("Memory Error");
return;
newNode-child = (struct K-aryTreeNode*) malloc( k* sizeof(struct K-aryTreeNode)); if(!newNode-child) {
printf("Memory Error");
return;
}
newNode-data = A[Ind);
for (int i=0; i<k; i++){
if(k Ind + i<n) { Ind++;
newNode-child[i]= BuildK-aryTree(A, n, k,Ind);
else newNode-child[i] =NULL;
}
return newNode;
Time Complexity: O(n), where n is the size of the pre-order array. This is because we are moving sequentially and not visiting the already constructed nodes.
6.8 Threaded Binary Tree Traversals (Stack or Queue-less Traversals)
In earlier sections we have seen that, preorder, inorder and postorder binary tree traversals used stacks and level order traversals used queues as an auxiliary data structure. In this section we will discuss new traversal algorithms which do not need both stacks and queues. Such traversal algorithms are called threaded binary tree traversals or stack/queue – less traversals.
Issues with Regular Binary Tree Traversals
• The storage space required for the stack and queue is large.
• The majority of pointers in any binary tree are NULL. For example, a binary tree with n nodes has n + 1 NULLpointers and these were wasted
• It is difficult to find successor node (preorder, inorder and postorder successors) fora given node
Motivation for Threaded Binary Trees
To solve these problems, one idea is to store some useful information in NULL pointers. If we observe the previous traversals carefully, stack/ queue is required because we have to record the current position in order to move to the right subtree after processing the left subtree. If we store the useful information in NULL pointers, then we don’t have to store such information in stack/ queue.
The binary trees which store such information in NULLpointers are called threaded binary trees. From the above discussion, let us assume that we want to store some useful information in NULL pointers. The next question is what to store?
The common convention is to put predecessor/successor information. That means, if we are dealing with preorder traversals, then for a given node, NULL left pointer will contain preorder predecessor information and NULL right pointer will contain preorder successor information. These special pointers are called threads.
Classifying Threaded Binary Trees
The classification is based on whether we are storing useful information in both NULLpointers or
only in one of them.
• If we store predecessor information in NULL left pointers only, then we can callsuch binary trees left threaded binary trees.
• If we store successor information in NULL right pointers only, then we can call suchbinary trees right threaded binary trees.
• If we store predecessor information in NULL left pointers and successor informationin NULL right pointers, then we can call such binary trees fully threaded binarytrees or simply threaded binary trees.
Note: For the remaining discussion we consider only (fully) threaded binary trees.
Threaded Binary Tree structure
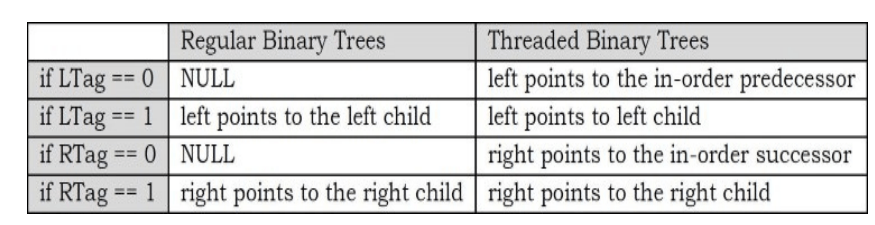
Any program examining the tree must be able to differentiate between a regular left/right pointer and a thread. To do this, we use two additional fields in each node, giving us, for threaded trees, nodes of the following form:

struct ThreadedBinaryTreeNode
struct ThreadedBinaryTreeNode "left;
int LTag:
int data;
int RTag:
struct ThreadedBinaryTreeNode "right;
Difference between Binary Tree and Threaded Binary Tree Structures
Note: Similarly, we can define preorder/postorder differences as well.
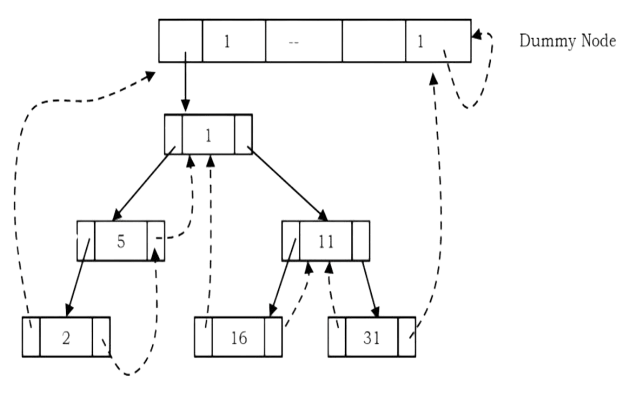
As an example, let us try representing a tree in inorder threaded binary tree form. The tree below shows what an inorder threaded binary tree will look like. The dotted arrows indicate the threads. If we observe, the left pointer of left most node (2) and right pointer of right most node (31) are hanging.
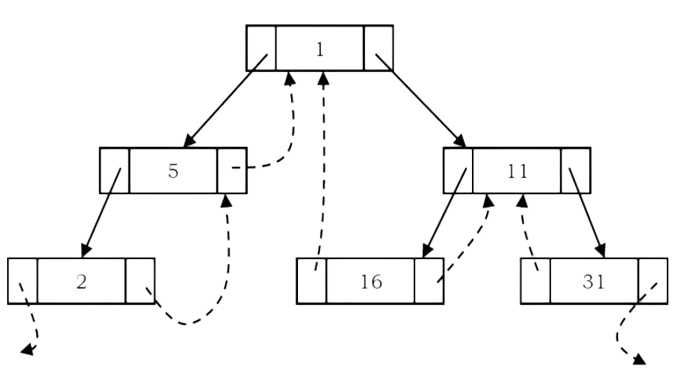
What should leftmost and rightmost pointers point to?
In the representation of a threaded binary tree, it is convenient to use a special node Dummy which is always present even for an empty tree. Note that right tag of Dummy node is 1 and its right child points to itself.

With this convention the above tree can be represented as:
Finding Inorder Successor in Inorder Threaded Binary Tree
To find inorder successor of a given node without using a stack, assume that the node for which we want to find the inorder successor is P.
Strategy: If P has a no right subtree, then return the right child of P. If P has right subtree, then return the left of the nearest node whose left subtree contains P
struct ThreadedBinaryTreeNode* InorderSuccessor(struct ThreadedBinaryTreeNode *P){
struct ThreadedBinaryTreeNode "Position;
if(P-RTag == 0)
return P→right;
else{
Position = P-right;
while(Position-LTag== 1)
Position = Position-left;
return Position;
}
Time Complexity: O(n). Space Complexity: O(1).
Inorder Traversal in Inorder Threaded Binary Tree
We can start with dummy node and call InorderSuccessor() to visit each node until we reach dummy node.
void InorderTraversal(struct ThreadedBinaryTreeNode *root){ struct ThreadedBinaryTreeNode *P = InorderSuccessor(root); while(P!= root) { P=InorderSuccessor(P); printf("%d", P-data);
Alternative coding
void InorderTraversal(struct ThreadedBinaryTreeNode *root){ struct ThreadedBinaryTreeNode *P = root;
while(1){
P = InorderSuccessor(P);
if(P== root) return; printf("%d",P-data);
}
Time Complexity: O(n). Space Complexity: O(1)
Finding PreOrder Successor in InOrder Threaded Binary Tree
Strategy: If P has a left subtree, then return the left child of P. If P has no left subtree, then return the right child of the nearest node whose right subtree contains P.
struct ThreadedBinaryTreeNode* PreorderSuccessor(struct ThreadedBinaryTreeNode *P){
struct ThreadedBinaryTreeNode *Position;
if(P-LTag == 1)
else {
return P-left;
Position = P;
while(Position RTag == 0)
Position Position-right;
return Position right;
Time Complexity: O(n). Space Complexity: O(1).
PreOrder Traversal of InOrder Threaded Binary Tree
As in inorder traversal, start with dummy node and call PreorderSuccessorf) to visit each node until we get dummy node again.
void PreorderTraversal(struct ThreadedBinaryTreeNode *root){ struct ThreadedBinaryTreeNode *P; P=PreorderSuccessor(root); while(P!=root) {
P = PreorderSuccessor(P);
printf("%d",P-data);
Alternative coding:
void PreorderTraversal(struct ThreadedBinaryTreeNode *root) { struct ThreadedBinaryTreeNode *P = root;
while(1)
P = PreorderSuccessor(P);
if(P == root) return;
printf("%d",P-data);
Time Complexity: O(n). Space Complexity: O(1).
Note: From the above discussion, it should be clear that inorder and preorder successor finding is easy with threaded binary trees. But finding postorder successor is very difficult if we do not use stack.
Insertion of Nodes in InOrder Threaded Binary Trees
For simplicity, let us assume that there are two nodes P and Q and we want to attach Q to right of
P. For this we will have two cases.
• Node P does not have right child: In this case we just need to attach Q to P and
change its left and right pointers.
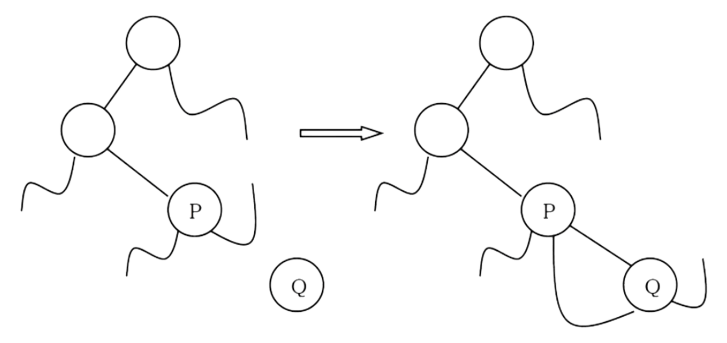
• Node P has right child (say, R): In this case we need to traverse R’s left subtree and find the left most node and then update the left and right pointer of that node (as shown below).
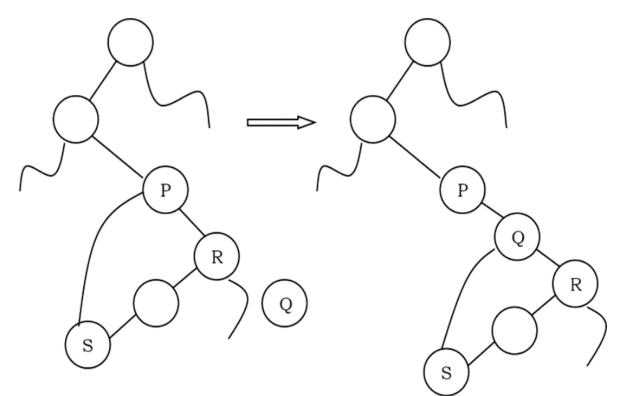
void InsertRightInInorderTBT(struct ThreadedBinaryTreeNode *P, struct ThreadedBinaryTreeNode *Q){ struct ThreadedBinaryTreeNode "Temp;
Q-right = P-right;
Q-RTag "P→RTag;
Q-left = P;
Q-LTag = 0;
P-right = Q;
P-RTag = 1;
if(Q-RTag == 1) {
//Case-2
Temp = Q-right; while(Temp→LTag)
Temp = Temp-left; Temp-left = Q;
Time Complexity: O(n). Space Complexity: O(1).
Threaded Binary Trees: Problems & Solutions
Problem-45 For a given binary tree (not threaded) how do we find the preorder successor?
Solution: For solving this problem, we need to use an auxiliary stack S. On the first call, the parameter node is a pointer to the head of the tree, and thereafter its value is NULL. Since we are simply asking for the successor of the node we got the last time we called the function.
It is necessary that the contents of the stack S and the pointer P to the last node “visited” are preserved from one call of the function to the next; they are defined as static variables
// pre-order successor for an unthreaded binary tree struct BinaryTreeNode *PreorderSuccessor(struct BinaryTreeNode *node){
static struct BinaryTreeNode *P; static Stack *S= CreateStack(); if(node != NULL)
P = node;
if(P-left != NULL) {
}
Push(S,P); P=P-left;
else{
1
while (P-right == NULL)
P = Pop(S);
P = P-right;
return P;
Problem-46 For a given binary tree (not threaded) how do we find the inorder successor?
Solution: Similar to the above discussion, we can find the inorder successor of a node as:
// In-order successor for an unthreaded binary tree struct BinaryTreeNode *InorderSuccessor(struct BinaryTreeNode *node){
static struct BinaryTreeNode *P;
static Stack *S= CreateStack();
if(node != NULL)
P = node; if(P-right == NULL)
else{
}
P = Pop(S);
P = P-right;
while (P-left != NULL) Push(S, P);
P = P-left;
return P;
6.9 Expression Trees
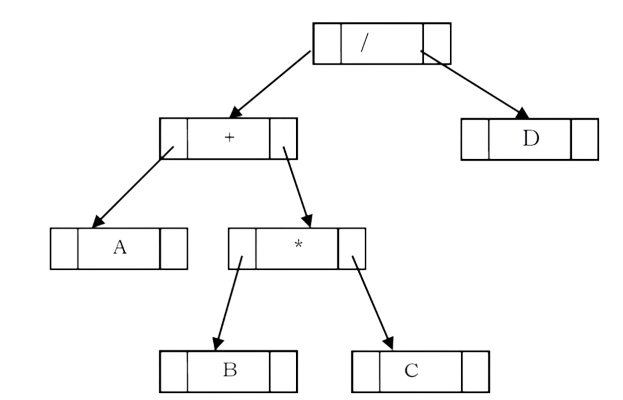
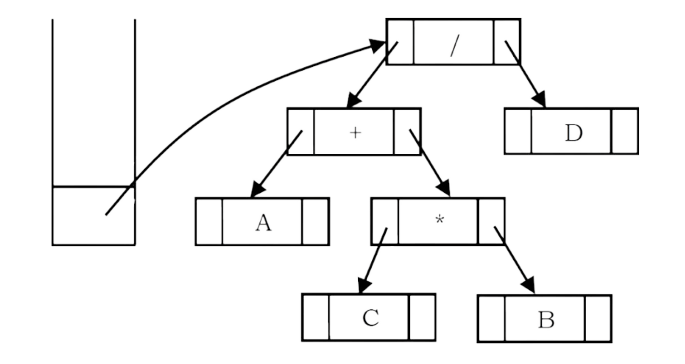
A tree representing an expression is called an expression tree. In expression trees, leaf nodes are operands and non-leaf nodes are operators. That means, an expression tree is a binary tree where internal nodes are operators and leaves are operands. An expression tree consists of binary expression. But for a u-nary operator, one subtree will be empty. The figure below shows a simple expression tree for (A + B * C) / D.
Algorithm for Building Expression Tree from Postfix Expression
struct Binary TreeNode *BuildExprTree(char postfixExpr[], int size){ struct Stack *S= Stack(size);
for (int i=0; i< size; i++){
}
if(postfixExpr[i] is an operand) {
}
struct Binary TreeNode newNode = (struct BinaryTreeNode")
malloc(sizeof (struct BinaryTreeNode));
if(!newNode) {
printf("Memory Error");
return NULL;
newNode-data -postfixExpr[i];
newNode-left = newNode-right = NULL;
Push(S, newNode);
else{
struct BinaryTreeNode *T2 = Pop(S), T1 = Pop(S);
struct BinaryTreeNode newNode = (struct BinaryTreeNode*) malloc(sizeof(struct BinaryTreeNode));
if(!newNode) {
printf("Memory Error");
return NULL;
}
newNode-data = postfixExpr[i];
newNode-left = T1;
newNode-right = T2; Push(S, newNode);
return S;
Example: Assume that one symbol is read at a time. If the symbol is an operand, we create a tree node and push a pointer to it onto a stack. If the symbol is an operator, pop pointers to two trees T1 and T2 from the stack (T1 is popped first) and form a new tree whose root is the operator and whose left and right children point to T2 and T1 respectively. A pointer to this new tree is then pushed onto the stack.
As an example, assume the input is A B C * + D /. The first three symbols are operands, so create tree nodes and push pointers to them onto a stack as shown below.
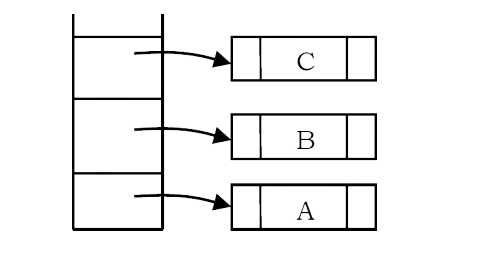
Next, an operator ‘*’ is read, so two pointers to trees are popped, a new tree is formed and a pointer to it is pushed onto the stack.
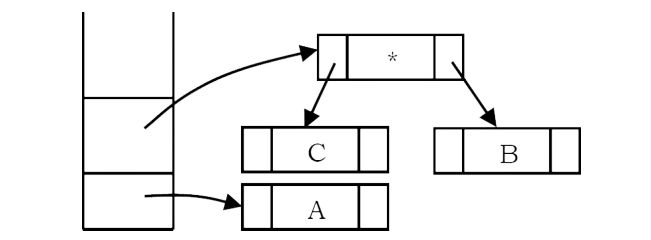
Next, an operator ‘+’ is read, so two pointers to trees are popped, a new tree is formed and a pointer to it is pushed onto the stack.
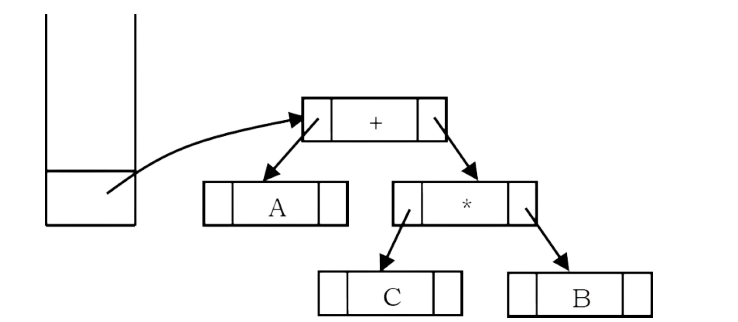
Next, an operand ‘D’ is read, a one-node tree is created and a pointer to the corresponding tree is pushed onto the stack.
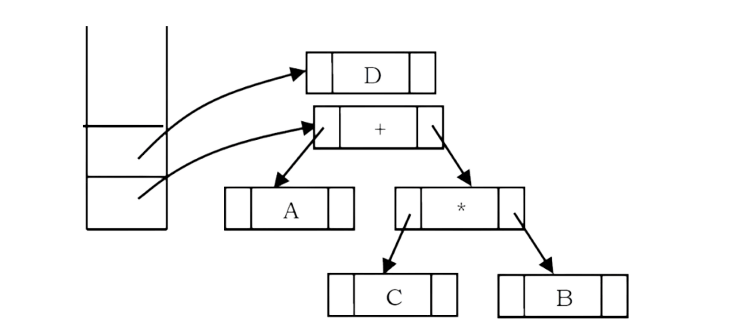
Finally, the last symbol (‘/’) is read, two trees are merged and a pointer to the final tree is left on the stack.
6.10 XOR Trees
This concept is similar to memory efficient doubly linked lists of Linked Lists chapter. Also, like threaded binary trees this representation does not need stacks or queues for traversing the trees. This representation is used for traversing back (to parent) and forth (to children) using ⊕ operation. To represent the same in XOR trees, for each node below are the rules used for representation:
• Each nodes left will have the ⊕ of its parent and its left children
• Each nodes right will have the ⊕ of its parent and its right children.
• The root nodes parent is NULLand also leaf nodes children are NULLnodes.
Based on the above rules and discussion, the tree can be represented as:
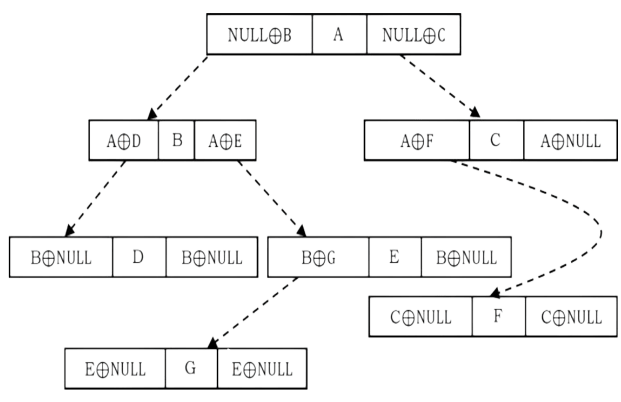
The major objective of this presentation is the ability to move to parent as well to children. Now, let us see how to use this representation for traversing the tree. For example, if we are at node B and want to move to its parent node A, then we just need to perform ⊕ on its left content with its left child address (we can use right child also for going to parent node).
Similarly, if we want to move to its child (say, left child D) then we have to perform ⊕ on its left content with its parent node address. One important point that we need to understand about thisrepresentation is: When we are at node B, how do we know the address of its children D? Since the traversal starts at node root node, we can apply ⊕ on root’s left content with NULL. As aresult we get its left child, B. When we are at B, we can appl ⊕ on its left content with Aaddress.
6.11 Binary Search Trees (BSTs)
Why Binary Search Trees?
In previous sections we have discussed different tree representations and in all of them we did not impose any restriction on the nodes data. As a result, to search for an element we need tocheck both in left subtree and in right subtree. Due to this, the worst case complexity of searchoperation is O(n).
In this section, we will discuss another variant of binary trees: Binary Search Trees (BSTs). Asthe name suggests, the main use of this representation is for searching. In this representation weimpose restriction on the kind of data a node can contain. As a result, it reduces the worst caseaverage search operation to O(logn).
Binary Search Tree Property
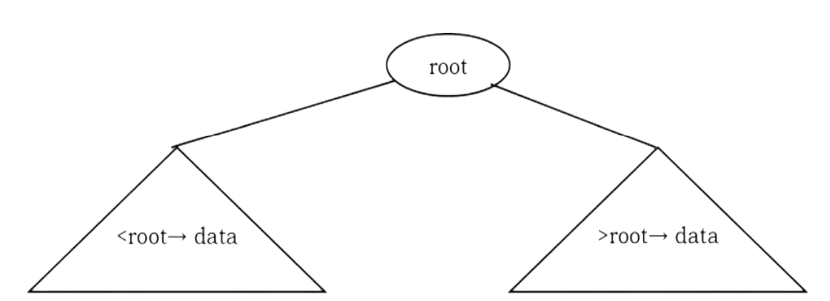
In binary search trees, all the left subtree elements should be less than root data and all the right subtree elements should be greater than root data. This is called binary search tree property. Note that, this property should be satisfied at every node in the tree.
• The left subtree of a node contains only nodes with keys less than the nodes key.
• The right subtree of a node contains only nodes with keys greater than the nodes key.
• Both the left and right subtrees must also be binary search trees.
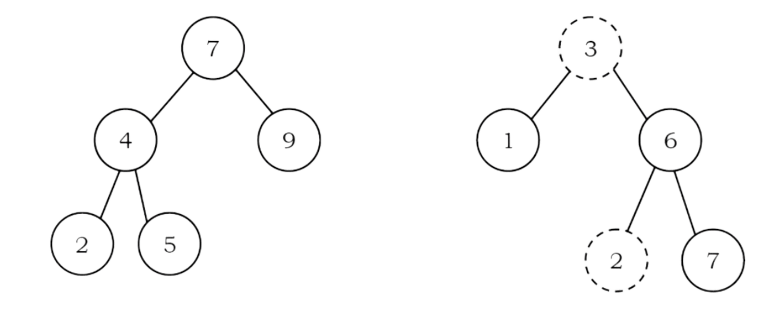
Example: The left tree is a binary search tree and the right tree is not a binary search tree (at
node 6 it’s not satisfying the binary search tree property
Binary Search Tree Declaration
There is no difference between regular binary tree declaration and binary search tree declaration. The difference is only in data but not in structure. But for our convenience we change the structure name as
struct BinarySearchTreeNode{ int data;
struct BinarySearchTreeNode *left; struct Binary SearchTreeNode *right;
Operations on Binary Search Trees
Main operations: Following are the main operations that are supported by binary search trees:
• Find/ Find Minimum / Find Maximum element in binary search trees
• Inserting an element in binary search trees
• Deleting an element from binary search trees
Auxiliary operations: Checking whether the given tree is a binary search tree or not
• Finding k th -smallest element in tree
• Sorting the elements of binary search tree and many more
Important Notes on Binary Search Trees
• Since root data is always between left subtree data and right subtree data, performing inorder traversal on binary search tree produces a sorted list.
• While solving problems on binary search trees, first we process left subtree, then root data, and finally we process right subtree. This means, depending on the problem, only the intermediate step (processing root data) changes and we do not touch the first and third steps.
• If we are searching for an element and if the left subtree root data is less than the element we want to search, then skip it. The same is the case with the right subtree.. Because of this, binary search trees take less time for searching an element than regular binary trees. In other words, the binary search trees consider either left or right subtrees for searching an element but not both.
• The basic operations that can be performed on binary search tree (BST) are insertion of element, deletion of element, and searching for an element. While performing these operations on BST the height of the tree gets changed each time. Hence there exists variations in time complexities of best case, average case, and worst case.
• The basic operations on a binary search tree take time proportional to the height of the tree. For a complete binary tree with node n, such operations runs in O(lgn) worst-case time. If the tree is a linear chain of n nodes (skew-tree), however, the same operations takes O(n) worst- case time
Finding an Element in Binary Search Trees
Find operation is straightforward in a BST. Start with the root and keep moving left or right using
the BST property. If the data we are searching is same as nodes data then we return current node.
If the data we are searching is less than nodes data then search left subtree of current node;
otherwise search right subtree of current node. If the data is not present, we end up in a NULL
link.
struct Binary SearchTreeNode *Find(struct BinarySearch TreeNode *root, int data){ if(root == NULL) return NULL;
if( data <root-data)
return Find(root-left, data);
else if data> root-data)
return( Find(root-right, data); return root;
Time Complexity: O(n), in worst case (when BST is a skew tree). Space Complexity: O(n), for recursive stack.
Non recursive version of the above algorithm can be given as:
struct BinarySearchTreeNode *Find(struct BinarySearch TreeNode *root, int data){
if( root == NULL)
return NULL;
while (root){
if(data == root-data)
return root;
else if(data> root-data)
root = root-right;
else root = root-left;
return NULL;
Time Complexity: O(n). Space Complexity: O(1).
Finding Minimum Element in Binary Search Trees
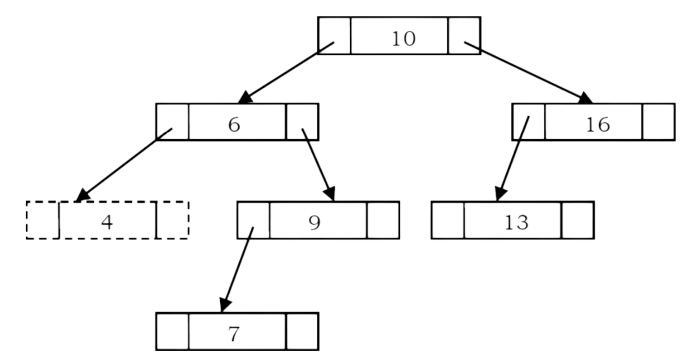
In BSTs, the minimum element is the left-most node, which does not has left child. In the BST
below, the minimum element is 4.
struct Binary SearchTreeNode *FindMin(struct Binary Search TreeNode *root){ if(root == NULL) return NULL;
else if( root-left == NULL)
else
return root;
return FindMin( root-left);
Time Complexity: O(n), in worst case (when BST is a left skew tree). Space Complexity: O(n), for recursive stack.
Non recursive version of the above algorithm can be given as:
struct Binary Search TreeNode *FindMin(struct BinarySearch TreeNode* root) {
if( root == NULL) return NULL;
while(root-left!= NULL)
root = root-left;
return root;
Time Complexity: O(n). Space Complexity: O(1).
Finding Maximum Element in Binary Search Trees
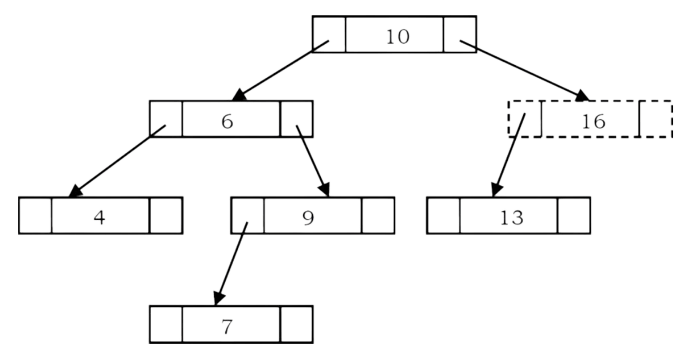
In BSTs, the maximum element is the right-most node, which does not have right child. In the BST
below, the maximum element is 16
struct Binary Search TreeNode *FindMax(struct BinarySearchTreeNode *root) {
if(root == NULL) return NULL;
else if( root-right == NULL) return root;
else return FindMax( root-right);
Time Complexity: O(n), in worst case (when BST is a right skew tree).
Space Complexity: O(n), for recursive stack.
Non recursive version of the above algorithm can be given as:
struct Binary Search TreeNode *FindMax(struct Binary Search TreeNode * root) {
if( root == NULL) return NULL;
while( root-right != NULL)
root = root-right;
return root;
Time Complexity: O(n). Space Complexity: O(1).
Where is Inorder Predecessor and Successor?
Where is the inorder predecessor and successor of node X in a binary search tree assuming all keys are distinct?
If X has two children then its inorder predecessor is the maximum value in its left subtree and its inorder successor the minimum value in its right subtree.
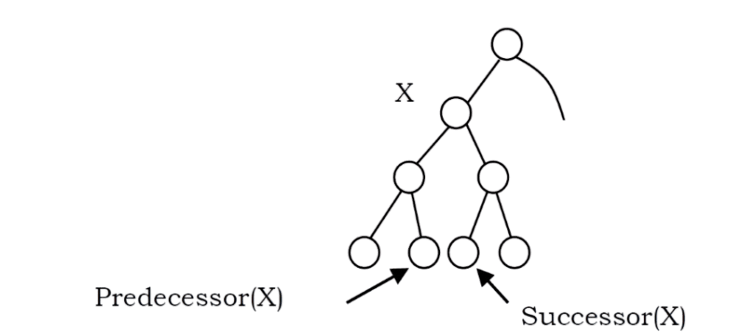
If it does not have a left child, then a node’s inorder predecessor is its first left ancestor

nserting an Element from Binary Search Tree

To insert data into binary search tree, first we need to find the location for that element. We can find the location of insertion by following the same mechanism as that of find operation. While finding the location, if the data is already there then we can simply neglect and come out. Otherwise, insert data at the last location on the path traversed.
As an example let us consider the following tree. The dotted node indicates the element (5) to be inserted. To insert 5, traverse the tree using find function. At node with key 4, we need to go right, but there is no subtree, so 5 is not in the tree, and this is the correct location for insertion
struct Binary SearchTreeNode *Insert(struct BinarySearch TreeNode *root, int data) {
==)
if(root == NULL) {
root (struct BinarySearchTreeNode *) malloc(sizeof(struct BinarySearchTreeNode));
if( root ==
NULL){ printf("Memory Error");
return;
}
else{
}
else {
root-data = data;
root-left root-right = NULL;
if(data < root-data)
root-left Insert(root-left, data); else if( data > root-data)
root-right Insert(root-right, data);
return root;
Note: In the above code, after inserting an element in subtrees, the tree is returned to its parent. As a result, the complete tree will get updated.
Time Complexity:O(n). Space Complexity:O(n), for recursive stack. For iterative version, space complexity is O(1).
Deleting an Element from Binary Search Tree
The delete operation is more complicated than other operations. This is because the element to be deleted may not be the leaf node. In this operation also, first we need to find the location of the element which we want to delete.
Once we have found the node to be deleted, consider the following cases:
• If the element to be deleted is a leaf node: return NULL to its parent. That means make the corresponding child pointer NULL. In the tree below to delete 5, set NULL to its parent node 2

• If the element to be deleted has one child: In this case we just need to send the current node’s child to its parent. In the tree below, to delete 4, 4 left subtree is set to its parent node 2.
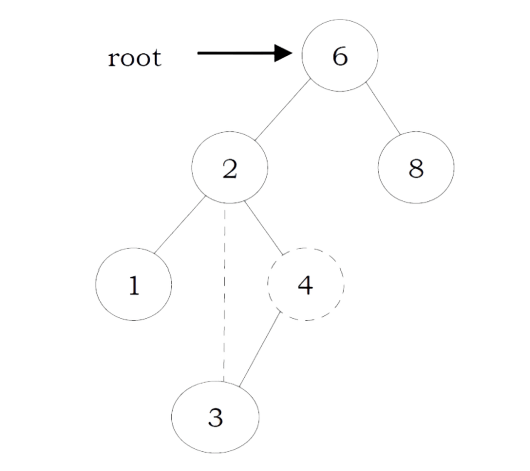
• If the element to be deleted has both children: The general strategy is to replace the key of this node with the largest element of the left subtree and recursively delete that node (which is now empty). The largest node in the left subtree cannot have a right child, so the second delete is an easy one. As an example, let us consider the following tree. In the tree below, to delete 8, it is the right child of the root. The key value is 8. It is replaced with the largest key in its left subtree (7), and then that node is deleted as before (second case).
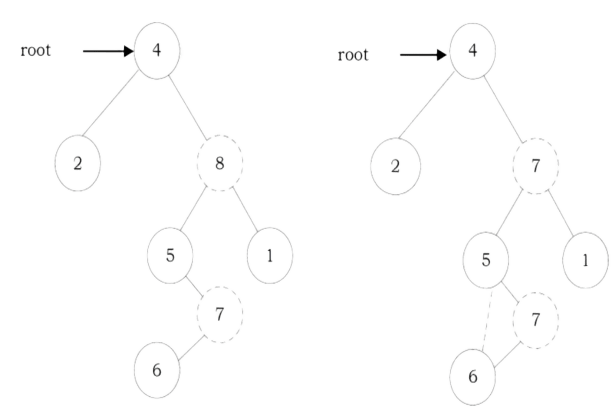
Note: We can replace with minimum element in right subtree also
struct BinarySearchTreeNode *Delete(struct BinarySearchTreeNode *root, int data) {
struct BinarySearchTreeNode *temp;
if( root == NULL)
printf("Element not there in tree");
else if(data < root-data)
root-left Delete(root-left, data);
else if(data > root-data)
root-right Delete(root-right, data);
else{
1
//Found element
if( root-left && root-right) {
/* Replace with largest in left subtree "/ temp FindMax( root-left); root-data = temp-data;
else {
=
root-left Delete(root-left, root-data);
/* One child */ temp = root;
if( root-left = NULL)
root root-right;
if root-right == NULL) root root-left;
free temp);
return root;
Time Complexity: O(n). Space Complexity: O(n) for recursive stack. For iterative version, space complexity is O(1).
Binary Search Trees: Problems & Solutions
Note: For ordering related problems with binary search trees and balanced binary search trees,
Inorder traversal has advantages over others as it gives the sorted order.
Problem-47 Given pointers to two nodes in a binary search tree, find the lowest common
ancestor (LCA). Assume that both values already exist in the tree.
Solution:
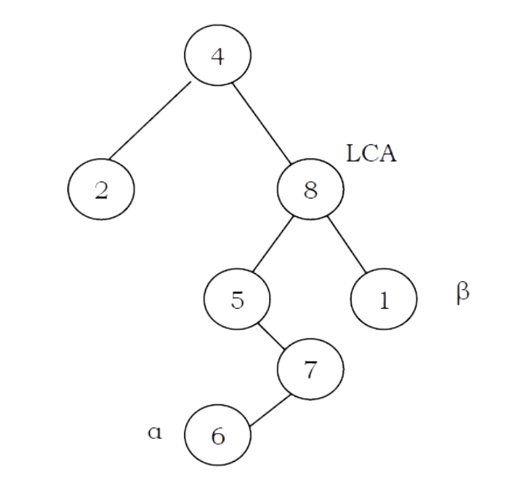
The main idea of the solution is: while traversing BST from root to bottom, the first node we encounter with value between α and β, i.e., α < node → data < β, is the Least Common Ancestor(LCA) of α and β (where α < β). So just traverse the BST in pre-order, and if we find a node with value in between α and β, then that node is the LCA. If its value is greater than both α and β, then the LCA lies on the left side of the node, and if its value is smaller than both α and β, then the LCA lies on the right side
struct BinarySearchTreeNode *FindLCA(struct BinarySearchTreeNode *root, struct BinarySearch TreeNode *a, struct BinarySearchTreeNode * B) {
while(1){
if((a-data < root-data && ß-data > root-data) ||
return root; if(a-data < root-data) root = root-left;
else root = root-right;
(a-data > root-data && B-data < root-datall
Time Complexity: O(n). Space Complexity: O(n), for skew trees.
Problem-48 Give an algorithm for finding the shortest path between two nodes in a BST.
Solution:It’s nothing but finding the LCA of two nodes in BST.
Problem-49 Give an algorithm for counting the number of BSTs possible with n nodes.
Solution: This is a DP problem. Refer to chapter on Dynamic Programming for the algorithm.
Problem-50 Give an algorithm to check whether the given binary tree is a BST or not.
Solution:
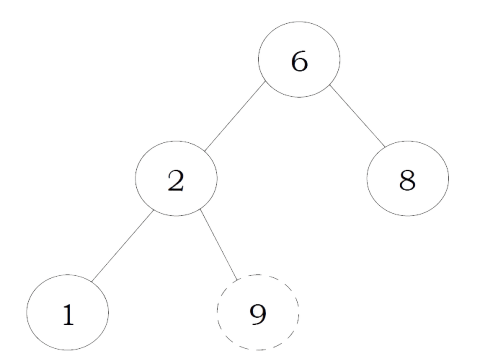
Consider the following simple program. For each node, check if the node on its left is smaller and check if the node on its right is greater. This approach is wrong as this will return true for binary tree below. Checking only at current node is not enough.
int ISBST(struct BinaryTreeNode* root) { if(root == NULL) return 1;
// false if left is > than root
if(root-left!= NULL && root-left-data > root-data) return 0;
// false if right is < than root
if(root-right != NULL && root-right-data < root-data) return 0;
//false if, recursively, the left or right is not a BST if(!IsBST(root-left) || !IsBST(root-right))
return 0;
// passing all that, it's a BST
return 1;
Problem-51 Can we think of getting the correct algorithm?
Solution: For each node, check if max value in left subtree is smaller than the current node data and min value in right subtree greater than the node data. It is assumed that we have helper functions FindMin() and FindMax() that return the min or max integer value from a non-empty tree.
/* Returns true if a binary tree is a binary search tree */ int ISBST(struct BinaryTreeNode* root) {
if(root == NULL) return 1;
/* false if the max of the left is > than root */ if(root-left != NULL && FindMax(root-left) > root-data) return 0;
/* false if the min of the right is <= than root */ if(root-right != NULL && FindMin(root-right) < root-data)
return 0;
/* false if, recursively, the left or right is not a BST */ if(!IsBST(root-left) || !IsBST(root-right)) return 0;
/* passing all that, it's a BST */
return 1;
Time Complexity: O(n 2 ). Space Complexity: O(n).
Problem-52 Can we improve the complexity of Problem-51?
Solution: Yes. A better solution is to look at each node only once. The trick is to write a utility helper function IsBSTUtil(struct BinaryTreeNode* root, int min, int max) that traverses down the tree keeping track of the narrowing min and max allowed values as it goes, looking at each node only once. The initial values for min and max should be INT_MIN and INT_MAX – they narrow from there
Initial call: IsBST(root, INT_MIN, INT_MAX);
int ISBST(struct BinaryTreeNode *root, int min, int max) {
if(!root) return 1;
return (root-data >min && root-data < max &&
IsBSTUtil(root-left, min, root-data) &&
IsBSTUtil(root-right, root-data, max));
Problem-53 Can we further improve the complexity of Problem-51?
Solution: Yes, by using inorder traversal. The idea behind this solution is that inorder traversal of
BST produces sorted lists. While traversing the BST in inorder, at each node check the condition
that its key value should be greater than the key value of its previous visited node. Also, we need
to initialize the prev with possible minimum integer value (say, INT_MIN).
int prev = INT_MIN;
int ISBST(struct BinaryTreeNode *root, int *prev) { if(!root) return 1;
if(!IsBST(root-left, prev)) return 0;
if(root-data < *prev) return 0; "prev=root-data;
return ISBST(root-right, prev);
Time Complexity: O(n). Space Complexity: O(n), for stack space.
Problem-54 Give an algorithm for converting BST to circular DLL with space complexity O(1).
Solution: Convert left and right subtrees to DLLs and maintain end of those lists. Then, adjust the pointers.
struct BinarySearch TreeNode *BST2DLL(struct BinarySearchTreeNode *root, struct BinarySearch TreeNode **Ltail) {
struct BinarySearchTreeNode "left, "Itail, "right, "*rtail;
if(root){
Itail NULL;
}
return NULL;
left BST2DLL(root-left, <ail);
right BST2DLL(root-right, &rtail);
=
root-left = Itail;
root-right = right;
if(!right)
else{
*Itail=root;
right-left = root;
* Itail = rtail;
if(!left)
else{
return root;
Itail-right = root; return left;
Time Complexity: O(n).
Problem-55 For Problem-54, is there any other way of solving it?
Solution: Yes. There is an alternative solution based on the divide and conquer method which is quite neat.
struct BinarySearchTreeNode "Append(struct BinarySearch TreeNode *a, struct Binary Search TreeNode *b) { struct BinarySearchTreeNode *aLast, *bLast;
}
if (a==NULL) return b; if (b==NULL)
return a;
alast= =a-left; blast-b-left; aLast-right = b; b-left = aLast;
bLast-right = a; a-left-blast;
return a;
struct BinarySearch TreeNode* TreeToList(struct BinarySearch TreeNode *root) {
struct BinarySearchTreeNode *aList, "bList;
if (root==NULL) return NULL;
aList TreeToList(root-left);
=
bList TreeToList(root-right);
root-left = root; root-right = root;
aList = Append(aList, root); aList = Append(aList, bList); return(aList);
Time Complexity: O(n).
Problem-56 Given a sorted doubly linked list, give an algorithm for converting it into balanced binary search tree.
Solution: Find the middle node and adjust the pointers.
*
struct DLLNode DLL to BalancedBST(struct DLLNode "head){
struct DLLNode *temp, *p, *q;
if(!head || !head-next) return head;
temp = FindMiddleNode(head); p = head;
while(p-next!= temp) p = p->next; p-next = NULL;
q = temp->next; temp->next = NULL;
=
temp-prev DLLtoBalancedBST(head);
=
temp-next DLLtoBalancedBST(q);
return temp;
Time Complexity: 2T(n/2) + O(n) [for finding the middle node] = O(nlogn).
Note: For FindMiddleNode function refer Linked Lists chapter.
Problem-57 Given a sorted array, give an algorithm for converting the array to BST.
Solution: If we have to choose an array element to be the root of a balanced BST, which element should we pick? The root of a balanced BST should be the middle element from the sorted array. We would pick the middle element from the sorted array in each iteration. We then create a node in the tree initialized with this element. After the element is chosen, what is left? Could you identify the sub-problems within the problem? There are two arrays left – the one on its left and the one on its right. These two arrays are the sub-problems of the original problem, since both of them are sorted. Furthermore, they are subtrees of the current node’s left and right child. The code below creates a balanced BST from the sorted array in O(n) time (n is the number of elements in the array). Compare how similar the code is to a binary search algorithm. Both are using the divide and conquer methodology
struct BinaryTreeNode *BuildBST(int A[], int left, int right){ struct BinaryTreeNode *newNode;
int mid;
if(left> right)
return NULL;
newNode = (struct BinaryTreeNode *)malloc(sizeof(struct BinaryTreeNode));
if(!newNode) { printf("Memory Error");
}
return;
if(left == right){
}
newNode-data = A[left];
newNode-left = newNode-right = NULL;
=
else{ mid left + (right-left)/2;
newNode-data = A[mid];
=
newNode-left BuildBST(A, left, mid-1); newNode-right = BuildBST(A, mid + 1, right);
return newNode;
Time Complexity: O(n). Space Complexity: O(n), for stack space.
Problem-58 Given a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST.
Solution: A naive way is to apply the Problem-56 solution directly. In each recursive call, we would have to traverse half of the list’s length to find the middle element. The run time complexity is clearly O(nlogn), where n is the total number of elements in the list. This is because each level of recursive call requires a total of n/2 traversal steps in the list, and there are a total of logn number of levels (ie, the height of the balanced tree).
Problem-59 For Problem-58, can we improve the complexity?
Solution: Hint: How about inserting nodes following the list order? If we can achieve this, we no longer need to find the middle element as we are able to traverse the list while inserting nodes to the tree.
Best Solution: As usual, the best solution requires us to think from another perspective. In other words, we no longer create nodes in the tree using the top-down approach. Create nodes bottomup, and assign them to their parents. The bottom-up approach enables us to access the list in its order while creating nodes [42].
Isn’t the bottom-up approach precise? Any time we are stuck with the top-down approach, we can give bottom-up a try. Although the bottom-up approach is not the most natural way we think, it is helpful in some cases. However, we should prefer top-down instead of bottom-up in general, since the latter is more difficult to verify.
Below is the code for converting a singly linked list to a balanced BST. Please note that the algorithm requires the list length to be passed in as the function parameters. The list length can be found in O(n) time by traversing the entire list once. The recursive calls traverse the list and create tree nodes by the list order, which also takes O(n) time. Therefore, the overall run time complexity is still O(n).
}
struct BinaryTreeNode* SortedListToBST(struct ListNode *& list, int start, int end) {
}
if(start > end) return NULL;
// same as (start+end)/2, avoids overflow
int mid start + (end-start)/2;
=
struct Binary TreeNode *leftChild SortedListToBST(list, start, mid-1); struct BinaryTreeNode*parent;
parent = (struct BinaryTreeNode *)malloc(sizeof(struct BinaryTreeNode));
if(!parent) {
printf("Memory Error");
return;
parent-data-list-data;
parent-left-leftChild;
list-list->next;
parent-right = SortedListToBST(list, mid+1, end);
return parent;
struct BinaryTreeNode* SortedListToBST(struct ListNode *head, int n) { return SortedListToBST(head, 0, n-1);
Problem-60 Give an algorithm for finding the k th smallest element in BST.
Solution: The idea behind this solution is that, inorder traversal of BST produces sorted lists. While traversing the BST in inorder, keep track of the number of elements visited.
struct BinarySearchTreeNode "kthSmallestInBST(struct BinarySearchTreeNode *root, int k, int *count){ if(!root)
return NULL;
struct BinarySearchTreeNode "left = kthSmallestInBST(root-left, k, count);
if left) return left; if(++count == k)
return root;
return kthSmallestInBST(root-right, k, count);
Time Complexity: O(n). Space Complexity: O(1).
Problem-61 Floor and ceiling: If a given key is less than the key at the root of a BST then the floor of the key (the largest key in the BST less than or equal to the key) must be in the left subtree. If the key is greater than the key at the root, then the floor of the key could be in the right subtree, but only if there is a key smaller than or equal to the key in the right subtree; if not (or if the key is equal to the the key at the root) then the key at the root is the floor of the key. Finding the ceiling is similar, with interchanging right and left. For example, if the sorted with input array is {1, 2, 8, 10, 10, 12, 19}, then
For x = 0: floor doesn’t exist in array, ceil = 1,
For x = 1: floor = 1, ceil = 1 For x = 5: floor =2, ceil = 8, For x = 20: floor = 19, ceil doesn’t exist in array
Solution: The idea behind this solution is that, inorder traversal of BST produces sorted lists. While traversing the BST in inorder, keep track of the values being visited. If the roots data is greater than the given value then return the previous value which we have maintained during traversal. If the roots data is equal to the given data then return root data.
1
struct BinaryTreeNode *FloorInBST(struct BinaryTreeNode *root, int data){ struct BinaryTreeNode *prev=NULL;
return FloorInBSTUtil(root, prev, data);
struct Binary TreeNode *FloorInBSTUtil(struct BinaryTreeNode *root,
if(!root)
struct BinaryTreeNode *prev, int data){
return NULL;
if(!FloorInBSTUtil(root-left, prev, data))
return 0;
if(root-data == data)
return root;
if(root-data > data)
return prev;
prev = root;
return FloorInBSTUtil(root-right, prev, data);
Time Complexity: O(n). Space Complexity: O(n), for stack space.
For ceiling, we just need to call the right subtree first, followed by left subtree.
}
struct BinaryTreeNode *CeilingInBST(struct BinaryTreeNode *root, int data){
struct BinaryTreeNode *prev=NULL;
return CeilingInBSTUtil(root, prev, data);
struct BinaryTreeNode *CeilingInBSTUtil(struct Binary TreeNode *root,
if(root)
struct BinaryTreeNode *prev, int data){
return NULL;
if(!CeilingInBSTUtil(root-right, prev, data))
return 0;
if(root-data == data)
return root;
if(root-data < data)
return prev;
prev = root;
return CeilingInBSTUtil(root-left, prev, data);
Time Complexity: O(n). Space Complexity: O(n), for stack space.
Problem-62 Give an algorithm for finding the union and intersection of BSTs. Assume parent pointers are available (say threaded binary trees). Also, assume the lengths of two BSTs are m and n respectively.
Solution: If parent pointers are available then the problem is same as merging of two sorted lists. This is because if we call inorder successor each time we get the next highest element. It’s just a matter of which InorderSuccessor to call. Time Complexity: O(m + n). Space complexity: O(1).
Problem-63 For Problem-62, what if parent pointers are not available?
Solution: If parent pointers are not available, the BSTs can be converted to linked lists and then merged.
1 Convert both the BSTs into sorted doubly linked lists in O(n + m) time. This produces 2 sorted lists.
2 Merge the two double linked lists into one and also maintain the count of total elements in O(n + m) time.
3 Convert the sorted doubly linked list into height balanced tree in O(n + m) time.
Problem-64 For Problem-62, is there any alternative way of solving the problem? Solution: Yes, by using inorder traversal.
• Perform inorder traversal on one of the BSTs.
• While performing the traversal store them in table (hash table).
• After completion of the traversal of first BST, start traversal of second BST and compare them with hash table contents.
Time Complexity: O(m + n). Space Complexity: O(Max(m,n)).
Problem-65 Given a BST and two numbers K1 and K2, give an algorithm for printing all the elements of BST in the range K1 and K2.
Solution:
void RangePrinter(struct BinarySearchTreeNode *root, int K1, int K2) {
if(root == NULL) return;
if(root-data> K1)
RangePrinter(root-left, K1, K2);
if(root-data> K1 && root-data <= K2) printf("%d", root-data);
if(root-data <= K2)
RangePrinter(root-right, K1, K2);
Time Complexity: O(n). Space Complexity: O(n), for stack space.
Problem-66 For Problem-65, is there any alternative way of solving the problem?
Solution: We can use level order traversal: while adding the elements to queue check for the range.
void Range SeachLevelOrder(struct BinarySearchTreeNode *root, int K1, int K2){
struct BinarySearchTreeNode *temp;
struct Queue Q CreateQueue();
if(root)
return NULL;
Q = EnQueue(Q, root);
while (!IsEmptyQueue(Q)) { temp-DeQueue(Q);
if(temp-data >= K1 && temp-data <= K2) printf("%d", temp-data);
if(temp-left && temp-data >= K1)
EnQueue(Q, temp-left);
if(temp-right && temp-data <= K2) EnQueue(Q, temp-right);
}
DeleteQueue(Q);
return NULL;
Time Complexity: O(n). Space Complexity: O(n), for queue.
Problem-67 For Problem-65, can we still think of an alternative way to solve the problem?
Solution: First locate K1 with normal binary search and after that use InOrder successor until we
encounter K2. For algorithm, refer to problems section of threaded binary trees.
Problem-68 Given root of a Binary Search tree, trim the tree, so that all elements returned in
the new tree are between the inputs A and B.
Solution: It’s just another way of asking Problem-65.
Problem-69 Given two BSTs, check whether the elements of them are the same or not. For
example: two BSTs with data 10 5 20 15 30 and 10 20 15 30 5 should return true and the
dataset with 10 5 20 15 30 and 10 15 30 20 5 should return false. Note: BSTs data can be
in any order.
Solution: One simple way is performing an inorder traversal on first tree and storing its data in
hash table. As a second step, perform inorder traversal on second tree and check whether that
data is already there in hash table or not (if it exists in hash table then mark it with -1 or some
unique value).
During the traversal of second tree if we find any mismatch return false. After traversal of second
tree check whether it has all -1s in the hash table or not (this ensures extra data available in
second tree).
Time Complexity: O(max(m, n)), where m and n are the number of elements in first and second
BST. Space Complexity: O(max(m,n)). This depends on the size of the first tree.
Problem-70 For Problem-69, can we reduce the time complexity?
Solution: Instead of performing the traversals one after the other, we can perform in – order
traversal of both the trees in parallel. Since the in – order traversal gives the sorted list, we can
check whether both the trees are generating the same sequence or not.
Time Complexity: O(max(m,n)). Space Complexity: O(1). This depends on the size of the first
tree.
Problem-71 For the key values 1… n, how many structurally unique BSTs are possible that
store those keys.
Solution: Strategy: consider that each value could be the root. Recursively find the size of the left
and right subtrees.
int CountTrees(int n) { if (n <= 1) return 1; else {
// there will be one value at the root, with whatever remains on the left and right
// each forming their own subtrees. Iterate through all the values that could be the root... int sum = 0;
int left, right, root;
for (root=1; root<=n; root++) {
leftCountTrees(root-1);
=
right CountTrees (numKeys - root);
// number of possible trees with this root == left right sum += left right;
}
return(sum);
Problem-72 Given a BST of size n, in which each node r has an additional field r → size, the number of the keys in the sub-tree rooted at r (including the root node r). Give an O(h) algorithm GreaterthanConstant(r,k) to find the number of keys that are strictly greater than k (h is the height of the binary search tree).
Solution:
int GreaterthanConstant (struct BinarySearchTreeNode *r, int k){
keysCount = 0
while (r!= Null){ if (k<r-data){
}
}
keysCount = keys Count + r-right-size + 1; r=r-left;
else if (k>r-data)
r = r-right;
else{ // k = r-key
keysCount = keys Count + r-right-size;
break;
}
return keys Count;
The suggested algorithm works well if the key is a unique value for each node. Otherwise when reaching k=r→data, we should start a process of moving to the right until reaching a node y with a key that is bigger then k, and then we should return keysCount + y→size. Time Complexity: O(h) where h=O(n) in the worst case and O(logn) in the average case.
6.12 Balanced Binary Search Trees
In earlier sections we have seen different trees whose worst case complexity is O(n), where n is the number of nodes in the tree. This happens when the trees are skew trees. In this section we will try to reduce this worst case complexity to O(logn) by imposing restrictions on the heights.
In general, the height balanced trees are represented with HB(k), where k is the difference between left subtree height and right subtree height. Sometimes k is called balance factor.
Full Balanced Binary Search Trees
In HB(k), if k = 0 (if balance factor is zero), then we call such binary search trees as full balanced binary search trees. That means, in HB(0) binary search tree, the difference between left subtree height and right subtree height should be at most zero. This ensures that the tree is a full binary tree. For example,
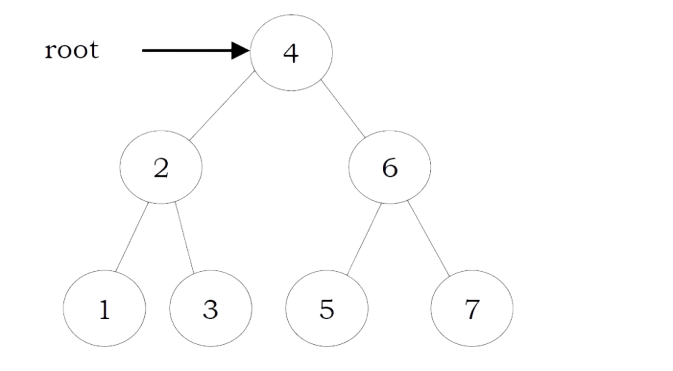
Note: For constructing HB(0) tree refer to Problems section.
6.13 AVL (Adelson-Velskii and Landis) Trees
In HB(k), if k = 1 (if balance factor is one), such a binary search tree is called an AVL tree. That means an AVL tree is a binary search tree with a balance condition: the difference between left subtree height and right subtree height is at most 1.
Properties of AVL Trees A binary tree is said to be an AVLtree, if:
• It is a binary search tree, and
• For any node X, the height of left subtree of X and height of right subtree of X differ by at most 1.
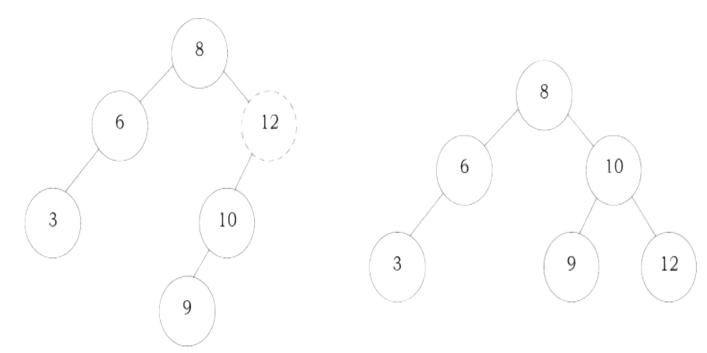
As an example, among the above binary search trees, the left one is not an AVL tree, whereas the right binary search tree is an AVLtree.
Minimum/Maximum Number of Nodes in AVL Tree
For simplicity let us assume that the height of an AVL tree is h and N(K) indicates the number of nodes in AVL tree with height h. To get the minimum number of nodes with height h, we should fill the tree with the minimum number of nodes possible. That means if we fill the left subtree with height h – 1 then we should fill the right subtree with height h – 2. As a result, the minimum number of nodes with height h is:
N(h) = N(h – 1) + N(h – 2) + 1
In the above equation:
• N(h – 1) indicates the minimum number of nodes with height h – 1.
• N(h – 2) indicates the minimum number of nodes with height h – 2.
• In the above expression, “1” indicates the current node.
We can give N(h – 1) either for left subtree or right subtree. Solving the above recurrence gives:
N(h) = N(h – 1) + N(h – 2) + 1
In the above equation:
• N(h – 1) indicates the minimum number of nodes with height h – 1.
• N(h – 2) indicates the minimum number of nodes with height h – 2.
• In the above expression, “1” indicates the current node.
We can give N(h – 1) either for left subtree or right subtree. Solving the above recurrence gives:
N(h) = N(h – 1) + N(h – 1) + 1 = 2N(h – 1) + 1
The above expression defines the case of full binary tree. Solving the recurrence we get:
N(h) = O( h) ⇒ h = logn ≈ O(logn)
∴ In both the cases, AVL tree property is ensuring that the height of an AVL tree with n nodes is
O(logn).
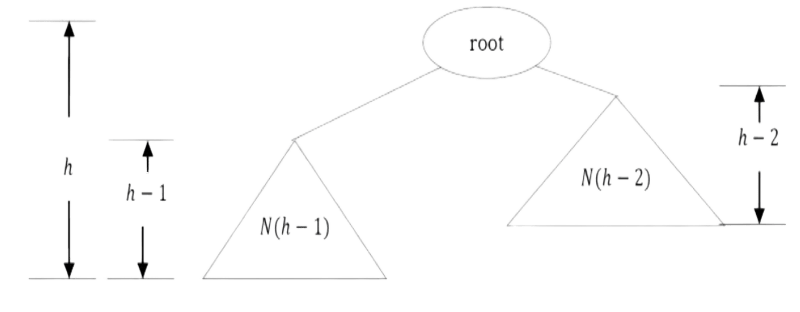
AVL Tree Declaration Since AVL tree is a BST, the declaration of AVL is similar to that of BST. But just to simplify the operations, we also include the height as part of the declaration
struct AVLTreeNode
struct AVLTreeNode *left; int data;
struct AVLTreeNode *right;
int height;
Finding the Height of an AVL tree
int Height(struct AVLTreeNode *root){
if(!root)
else
return -1;
return root-height;
Time Complexity: O(1)
Rotations
When the tree structure changes (e.g., with insertion or deletion), we need to modify the tree to restore the AVL tree property. This can be done using single rotations or double rotations. Since an insertion/deletion involves adding/deleting a single node, this can only increase/decrease the height of a subtree by 1.
So, if the AVL tree property is violated at a node X, it means that the heights of left(X) and right(X) differ by exactly 2. This is because, if we balance the AVL tree every time, then at any point, the difference in heights of left(X) and right(X) differ by exactly 2. Rotations is the technique used for restoring the AVL tree property. This means, we need to apply the rotations for the node X.
Observation: One important observation is that, after an insertion, only nodes that are on the path from the insertion point to the root might have their balances altered, because only those nodes have their subtrees altered. To restore the AVL tree property, we start at the insertion point and keep going to the root of the tree.
While moving to the root, we need to consider the first node that is not satisfying the AVL property. From that node onwards, every node on the path to the root will have the issue.
Also, if we fix the issue for that first node, then all other nodes on the path to the root will automatically satisfy the AVL tree property. That means we always need to care for the first node that is not satisfying the AVLproperty on the path from the insertion point to the root and fix it.
Types of Violations
Let us assume the node that must be rebalanced is X. Since any node has at most two children, and a height imbalance requires that X’s two subtree heights differ by two, we can observe that a violation might occur in four cases:
1. An insertion into the left subtree of the left child of X.
2. An insertion into the right subtree of the left child of X.
3. An insertion into the left subtree of the right child of X.
4. An insertion into the right subtree of the right child of X.
Cases 1 and 4 are symmetric and easily solved with single rotations. Similarly, cases 2 and 3 are also symmetric and can be solved with double rotations (needs two single rotations).
Single Rotations
Left Left Rotation (LL Rotation) [Case-1]: In the case below, node X is not satisfying the AVL tree property. As discussed earlier, the rotation does not have to be done at the root of a tree. In general, we start at the node inserted and travel up the tree, updating the balance information at every node on the path.
For example, in the figure above, after the insertion of 7 in the original AVL tree on the left, node 9 becomes unbalanced. So, we do a single left-left rotation at 9. As a result we get the tree on the right.
struct AVLTreeNode *SingleRotate Left(struct AVLTreeNode *X){ struct AVLTreeNode *W = X-left;
X-left = W-right;
W-right = X;
X-height = max( Height(X-left), Height(X-right)) + 1; W-height = max( Height(W-left), X-height) + 1; return W; /* New root */
Time Complexity: O(1). Space Complexity: O(1). Right Right Rotation (RR Rotation) [Case-4]: In this case, node X is not satisfying the AVL tree property
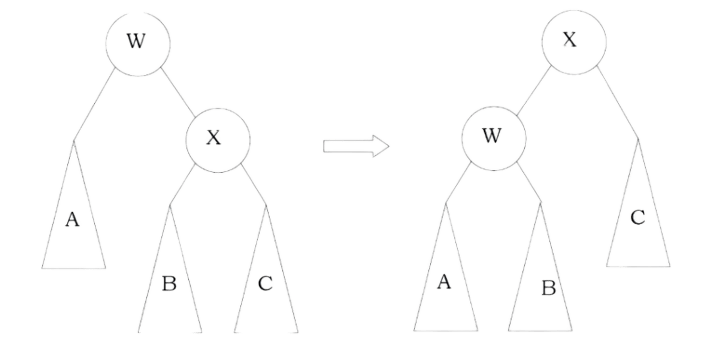
For example, in the figure, after the insertion of 29 in the original AVL tree on the left, node 15 becomes unbalanced. So, we do a single right-right rotation at 15. As a result we get the tree on the right
struct AVLTreeNode *SingleRotate Right(struct AVLTreeNode *W){ struct AVLTreeNode *X = W-right;
W-right = X-left; X-left = W;
W-height = max( Height(W-right), Height(W-left)) + 1; X-height = max( Height(X-right), W-height) + 1; return X;
Time Complexity: O(1). Space Complexity: O(1).
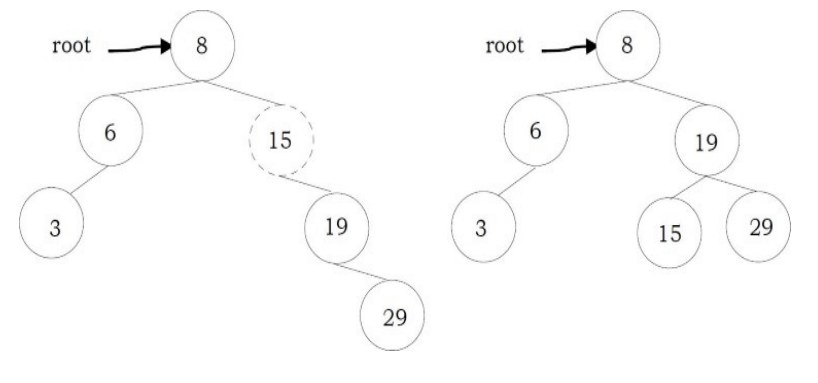
Double Rotations
Left Right Rotation (LR Rotation) [Case-2]: For case-2 and case-3 single rotation does not fix the problem. We need to perform two rotations.
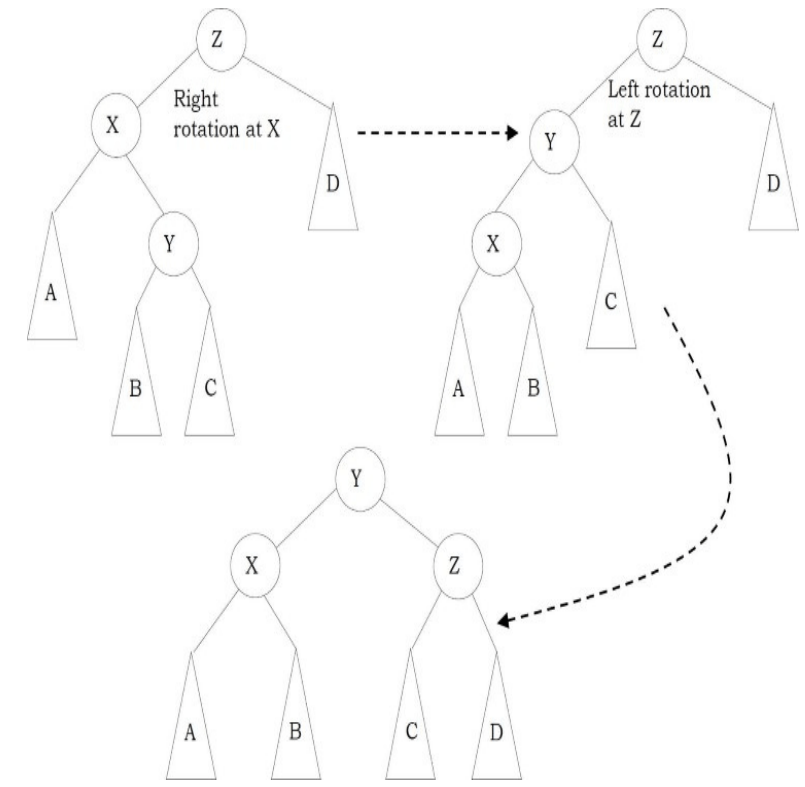
As an example, let us consider the following tree: The insertion of 7 is creating the case-2 scenario and the right side tree is the one after the double rotation
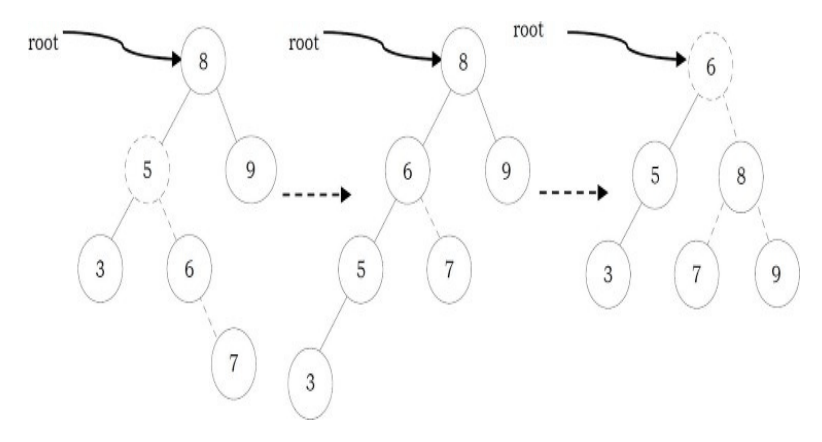
Code for left-right double rotation can be given as
struct AVLTreeNode *DoubleRotatewithLeft( struct AVLTreeNode *Z){
Z-left SingleRotateRight( Z-left);
return SingleRotateLeft(Z);
Right Left Rotation (RL Rotation) [Case-3]: Similar to case-2, we need to perform two rotations to fix this scenario

As an example, let us consider the following tree: The insertion of 6 is creating the case-3 scenario and the right side tree is the one after the double rotation.

Insertion into an AVL tree
Insertion into an AVL tree is similar to a BST insertion. After inserting the element, we just need to check whether there is any height imbalance. If there is an imbalance, call the appropriate rotation functions.
struct AVLTreeNode *Insert( struct AVLTreeNode *root, struct AVLTreeNode *parent, int data){
}
}
}
if(root){
}
root = (struct AVLTreeNode*) malloc(sizeof (struct AVLTreeNode*));
if(root)[
printf("Memory Error"); return NULL;
else {
root-data = data;
root-height = 0;
root-left root-right = NULL;
else if( data < root-data) {
root-left Insert( root-left, root, data);
if((Height( root-left)- Height( root-right)) == 2){ if( data < root-left-data)
root = SingleRotateLeft(root);
else root Double RotateLeft(root);
else if(data > root-data) {
root-right = Insert( root-right, root, data);
if((Height( root-right) - Height( root-left)) == 2) { if( data < root-right-data)
root = SingleRotateRight(root);
else root Double RotateRight(root);
/* Else data is in the tree already. We'll do nothing */ root-height = max( Height(root-left), Height(root-right)) + 1; return root;
Time Complexity: O(logn). Space Complexity: O(logn).
AVL Trees: Problems & Solutions
Problem-73 Given a height h, give an algorithm for generating the HB(0).
Solution: As we have discussed, HB(0) is nothing but generating full binary tree. In full binary
tree the number of nodes with height h is: 2
h+1 – 1 (let us assume that the height of a tree with one
node is 0). As a result the nodes can be numbered as: 1 to 2
h+1 – 1
struct BinarySearch TreeNode *BuildHBO (int h){ struct BinarySearchTreeNode *temp;
ifth == 0) return NULL;
temp = (struct BinarySearchTreeNode *)malloc (sizeof(struct BinarySearchTreeNode)); temp-left = BuildHBO (h-1);
temp-data = count++; //assume count is a global variable
temp-right = BuildHBO (h-1);
return temp;
Time Complexity: O(n). Space Complexity: O(logn), where logn indicates the maximum stack size which is equal to height of tree.
Problem-74 Is there any alternative way of solving Problem-73?
Solution: Yes, we can solve it following Mergesort logic. That means, instead of working with height, we can take the range. With this approach we do not need any global counter to be maintained
struct BinarySearch TreeNode *BuildHBO (int h){ struct BinarySearchTreeNode *temp;
ifth == 0) return NULL;
temp = (struct BinarySearchTreeNode *)malloc (sizeof(struct BinarySearchTreeNode)); temp-left = BuildHBO (h-1);
temp-data = count++; //assume count is a global variable
temp-right = BuildHBO (h-1);
return temp;
The initial call to the BuildHBO function could be: BuildHB0(1, 1 ≪ h). 1 ≪ h does the shift operation for calculating the 2 h+1 – 1.
Time Complexity: O(n). Space Complexity: O(login). Where logn indicates maximum stack size which is equal to the height of the tree.
Problem-75 Construct minimal AVL trees of height 0,1,2,3,4, and 5. What is the number of nodes in a minimal AVLtree of height 6?
Solution Let N(h) be the number of nodes in a minimal AVLtree with height h
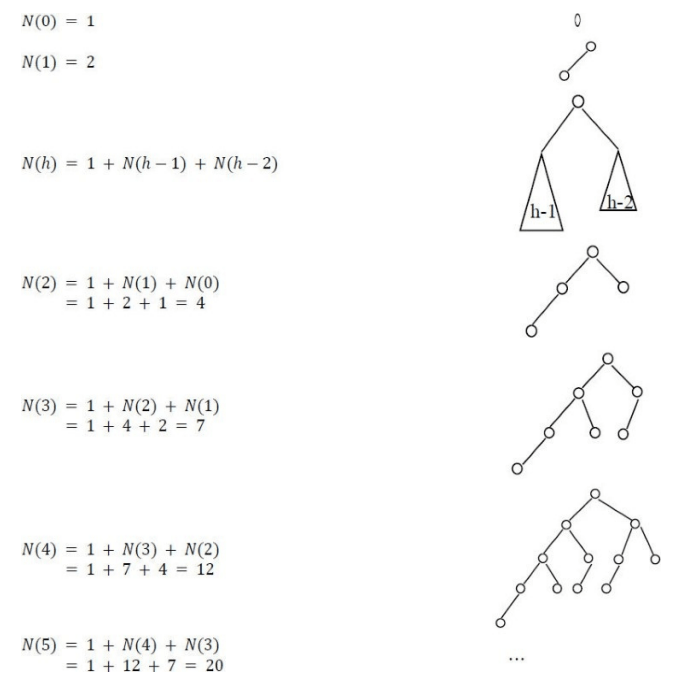
Problem-76 For Problem-73, how many different shapes can there be of a minimal AVL tree of height h?
Solution: Let NS(h) be the number of different shapes of a minimal AVLtree of height h.
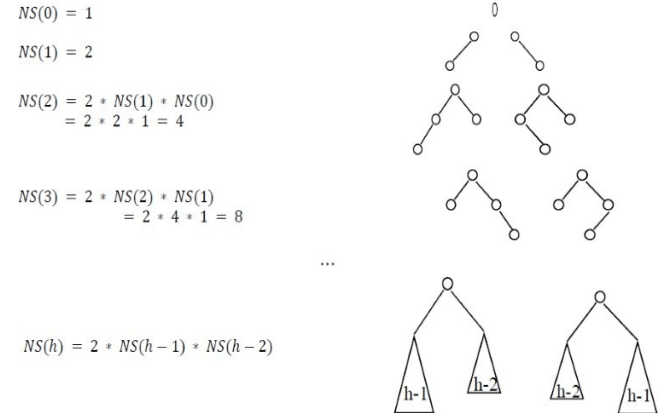
Problem-77 Given a binary search tree, check whether it is an AVLtree or not?
Solution: Let us assume that IsAVL is the function which checks whether the given binary search tree is an AVL tree or not. IsAVL returns –1 if the tree is not an AVL tree. During the checks each node sends its height to its parent.
struct Binary Search TreeNode *BuildHB0(int 1, int r){ struct BinarySearchTreeNode *temp;
int mid 1+
if( 1>r) return NULL;
temp = (struct BinarySearchTreeNode *)malloc (sizeof(struct BinarySearchTreeNode)); temp-data = mid;
=
temp-left BuildHB0(1, mid-1);
temp-right = BuildHB0(mid+1, r);
return temp;
Time Complexity: O(n). Space Complexity: O(n).
Problem-78 Given a height h, give an algorithm to generate an AVL tree with minimum number of nodes.
Solution: To get minimum number of nodes, fill one level with h – 1 and the other with h – 2
int IsAVL(struct BinarySearchTreeNode *root){ int left, right; if(root) return 0;
left = IsAVL(root-left);
if(left == -1) return left;
right = ISAVL/root-right); if(right == -1) return right; if(abs(left-right)>1)
return -1;
return Max(left, right)+1;
Problem-79 Given an AVL tree with n integer items and two integers a and b, where a and b can be any integers with a <= b. Implement an algorithm to count the number of nodes in the range [a,b].
Solution:
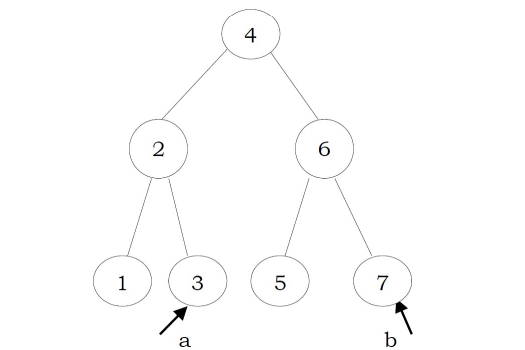
The idea is to make use of the recursive property of binary search trees. There are three cases to consider: whether the current node is in the range [a, b], on the left side of the range [a, b], or on the right side of the range [a,b]. Only subtrees that possibly contain the nodes will be processed under each of the three cases.
int RangeCount(struct AVLNode *root, int a, int b) { if(root == NULL) return 0; else if(root-data > b)
return RangeCount(root-left, a, b);
else if(root-data <a)
return RangeCount(root-right, a, b);
else if(root-data >= a && root-data <= b)
return RangeCount(root-left, a, b) + RangeCount(root-right, a, b) + 1;
The complexity is similar to in – order traversal of the tree but skipping left or right sub-trees when they do not contain any answers. So in the worst case, if the range covers all the nodes in the tree, we need to traverse all the n nodes to get the answer. The worst time complexity is therefore O(n).
If the range is small, which only covers a few elements in a small subtree at the bottom of the tree, the time complexity will be O(h) = O(logn), where h is the height of the tree. This is because only a single path is traversed to reach the small subtree at the bottom and many higher level subtrees have been pruned along the way
Note: Refer similar problem in BST.
Problem-80 Given a BST (applicable to AVL trees as well) where each node contains two data elements (its data and also the number of nodes in its subtrees) as shown below. Convert the tree to another BST by replacing the second data element (number of nodes in its subtrees) with previous node data in inorder traversal. Note that each node is merged with inorder previous node data. Also make sure that conversion happens in-place
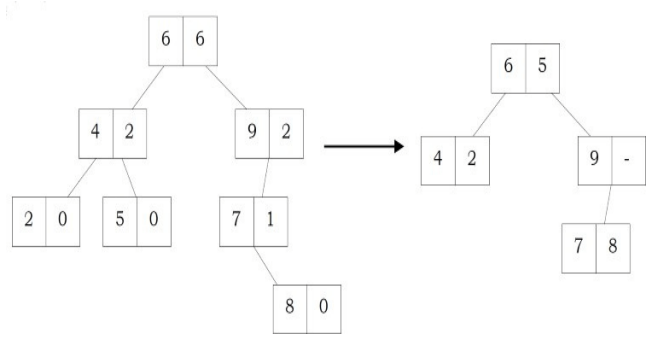
Solution: The simplest way is to use level order traversal. If the number of elements in the left subtree is greater than the number of elements in the right subtree, find the maximum element in the left subtree and replace the current node second data element with it. Similarly, if the number of elements in the left subtree is less than the number of elements in the right subtree, find the minimum element in the right subtree and replace the current node second data element with it.
struct BST "TreeCompression (struct BST *root){
struct BST *temp, "temp2;
struct Queue Q = CreateQueue();
if(!root) return;
EnQueue(Q, root);
while (!IsEmptyQueue(Q)){
temp = DeQueue(Q);
if(temp-left && temp-right && temp-left-data2> temp-right-data2)
temp2 - FindMax(temp);
else temp2 FindMin(temp);
temp-data2 temp2-data2; //Process current node
//Remember to delete this node.
DeleteNodeInBST(temp2);
if(temp-left)
EnQueue(Q, temp-left);
if(temp-right)
EnQueue(Q, temp-right);
}
DeleteQueue(Q);
Time Complexity: O(nlogn) on average since BST takes O(logn) on average to find the maximum or minimum element. Space Complexity: O(n). Since, in the worst case, all the nodes on the entire last level could be in the queue simultaneously.
Problem-81 Can we reduce time complexity for the previous problem?
Solution: Let us try using an approach that is similar to what we followed in Problem-60. The idea behind this solution is that inorder traversal of BST produces sorted lists. While traversing the BST in inorder, keep track of the elements visited and merge them
struct BinarySearchTreeNode TreeCompression(struct BinarySearchTreeNode 'root,
int "previousNodeData){
if(!root) return NULL; TreeCompression(root-left, previousNode);
if("previousNodeData == INT_MIN){
'previousNodeData = root-data;
free(root);
}
if("previous Node Data != INT_MIN){
//Process current node
root-data2 = previous NodeData;
"previousNode Data INT_MIN;
}
return TreeCompression(root-right, previousNode);
Time Complexity: O(n). Space Complexity: O(1). Note that, we are still having recursive stack space for inorder traversal.
Problem-82 Given a BST and a key, find the element in the BST which is closest to the given key.
Solution: As a simple solution, we can use level-order traversal and for every element compute the difference between the given key and the element’s value. If that difference is less than the previous maintained difference, then update the difference with this new minimum value. With this approach, at the end of the traversal we will get the element which is closest to the given key
int ClosestInBST(struct BinaryTreeNode *root, int key){ struct BinaryTreeNode *temp, *element; struct Queue *Q;
int difference INT_MAX;
if(root) return 0;
Q = CreateQueue(); EnQueue(Q,root); while (!IsEmptyQueue(Q)) { temp = DeQueue(Q);
if(difference (abs(temp-data-key)){ difference = abs(temp-data-key);
element = temp;
}
}
if(temp-left)
EnQueue (Q, temp-left);
if(temp-right)
EnQueue (Q, temp-right);
DeleteQueue(Q); return element-data;
Time Complexity: O(n). Space Complexity: O(n).
Problem-83 For Problem-82, can we solve it using the recursive approach?
Solution: The approach is similar to Problem-18. Following is a simple algorithm for finding the closest Value in BST.
1. If the root is NULL, then the closest value is zero (or NULL).
2. If the root’s data matches the given key, then the closest is the root.
3. Else, consider the root as the closest and do the following: a. If the key is smaller than the root data, find the closest on the left side tree of the root recursively and call it temp. b. If the key is larger than the root data, find the closest on the right side tree of the root recursively and call it temp.
4. Return the root or temp depending on whichever is nearer to the given key
struct BinaryTreeNode* ClosestInBST(struct BinaryTreeNode *root, int key){ struct BinaryTreeNode *temp;
if(root == NULL)
return root;
if(root-data == key)
return root; if(key < root-data){ if(!root-left) return root;
temp = ClosestInBST(root-left, key);
return abs(temp-data-key) > abs(root-data-key) ? root: temp;
}else{
}
if(!root-right)
return root;
temp = ClosestInBST(root-right, key);
return abs(temp-data-key) > abs(root-data-key) ? root: temp;
return NULL;
Time Complexity: O(n) in worst case, and in average case it is O(logn).
Space Complexity: O(n) in worst case, and in average case it is O(logn).
Problem-84 Median in an infinite series of integers
Solution: Median is the middle number in a sorted list of numbers (if we have odd number of elements). If we have even number of elements, median is the average of two middle numbers in a sorted list of numbers.
For solving this problem we can use a binary search tree with additional information at each node, and the number of children on the left and right subtrees. We also keep the number of total nodes in the tree. Using this additional information we can find the median in O(logn) time, taking the appropriate branch in the tree based on the number of children on the left and right of the current node. But, the insertion complexity is O(n) because a standard binary search tree can degenerate into a linked list if we happen to receive the numbers in sorted order.
So, let’s use a balanced binary search tree to avoid worst case behavior of standard binary search trees. For this problem, the balance factor is the number of nodes in the left subtree minus the number of nodes in the right subtree. And only the nodes with a balance factor of+ 1 or 0 are considered to be balanced.
So, the number of nodes on the left subtree is either equal to or 1 more than the number of nodes on the right subtree, but not less.
If we ensure this balance factor on every node in the tree, then the root of the tree is the median, if the number of elements is odd. In the number of elements is even, the median is the average of the root and its inorder successor, which is the leftmost descendent of its right subtree.
So, the complexity of insertion maintaining a balanced condition is O(logn) and finding a median operation is O(1) assuming we calculate the inorder successor of the root at every insertion if the number of nodes is even.
Insertion and balancing is very similar to AVLtrees. Instead of updating the heights, we update the number of nodes information. Balanced binary search trees seem to be the most optimal solution, insertion is O(logn) and find median is O(1).
Note: For an efficient algorithm refer to the Priority Queues and Heaps chapter.
Problem-85 Given a binary tree, how do you remove all the half nodes (which have only one child)? Note that we should not touch leaves.
Solution: By using post-order traversal we can solve this problem efficiently. We first process the left children, then the right children, and finally the node itself. So we form the new tree bottom up, starting from the leaves towards the root. By the time we process the current node, both its left and right subtrees have already been processed.
struct BinaryTreeNode *removeHalfNodes(struct BinaryTreeNode *root){
if (!root)
return NULL;
root-left-remove HalfNodes(root-left); root-right-removeHalfNodes(root-right);
if (root-left == NULL && root-right == NULL) return root;
if (root-left = NULL) return root-right;
if (root-right == NULL) return root-left;
return root;
Time Complexity: O(n).
Problem-86 Given a binary tree, how do you remove its leaves?
Solution: By using post-order traversal we can solve this problem (other traversals would also work).
struct BinaryTreeNode* removeLeaves(struct BinaryTreeNode* root) {
if (root != NULL) {
if (root-left == NULL && root-right == NULL) {
free(root);
return NULL;
} else {
root-left removeLeaves(root-left);
root-right = removeLeaves(root-right);
return root;
Time Complexity: O(n).
Problem-87 Given a BST and two integers (minimum and maximum integers) as parameters, how do you remove (prune) elements that are not within that range?
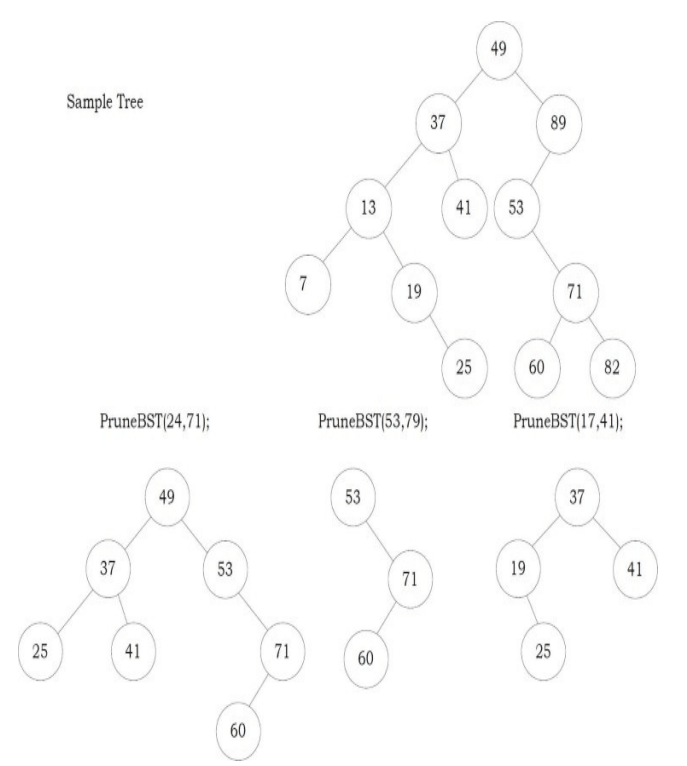
Solution: Observation: Since we need to check each and every element in the tree, and the subtree changes should be reflected in the parent, we can think about using post order traversal. So we process the nodes starting from the leaves towards the root. As a result, while processing the node itself, both its left and right subtrees are valid pruned BSTs. At each node we will return a pointer based on its value, which will then be assigned to its parent’s left or right child pointer, depending on whether the current node is the left or right child of the parent. If the current node’s value is between A and B (A <= node’s data <= B) then no action needs to be taken, so we return the reference to the node itself
If the current node’s value is less than A, then we return the reference to its right subtree and discard the left subtree. Because if a node’s value is less than A, then its left children are definitely less than A since this is a binary search tree. But its right children may or may not be less than A; we can’t be sure, so we return the reference to it. Since we’re performing bottom-up post-order traversal, its right subtree is already a trimmed valid binary search tree (possibly NULL), and its left subtree is definitely NULL because those nodes were surely less than A and they were eliminated during the post-order traversal.
A similar situation occurs when the node’s value is greater than B, so we now return the reference
to its left subtree. Because if a node’s value is greater than B, then its right children are definitely
greater than B. But its left children may or may not be greater than B; So we discard the right
subtree and return the reference to the already valid left subtree
struct BinarySearchTreeNode* PruneBST(struct BinarySearch TreeNode *root, int A, int B){
if(!root) return NULL;
root-left- PruneBST(root-left,A,B);
root-right PruneBST(root-right,A,B); if(A<=root-data && root-data<=B)
return root; if(root-data<A)
return root-right; if(root-data>B) return root-left;
Time Complexity: O(n) in worst case and in average case it is O(logn).
Note: If the given BST is an AVLtree then O(n) is the average time complexity.
Problem-88 Given a binary tree, how do you connect all the adjacent nodes at the same
level? Assume that given binary tree has next pointer along with left and right pointers as
shown below
struct BinaryTreeNode{ int data;
struct BinaryTreeNode *left;
struct BinaryTreeNode *right; struct BinaryTreeNode *next;
Solution: One simple approach is to use level-order traversal and keep updating the next pointers. While traversing, we will link the nodes on the next level. If the node has left and right node, we will link left to right. If node has next node, then link rightmost child of current node to leftmost child of next node.
void linkingNodesOfSame Level(struct BinaryTreeNode *root){
struct Queue *Q= CreateQueue();
struct BinaryTreeNode *prev; // Pointer to the previous node of the current level struct BinaryTreeNode *temp;
int currentLevelNodeCount, nextLevelNodeCount;
if(root) return;
EnQueue(Q, root);
currentLevelNodeCount = 1;
nextLevelNodeCount = 0;
prev = NULL;
while (!IsEmptyQueue(Q)) { temp = DeQueue(Q); if (temp-left){
}
EnQueue(Q, temp-left);
nextLevelNodeCount++;
if (temp-right){
EnQueue(Q, temp-right);
nextLevelNodeCount++;
// Link the previous node of the current level to this node if (prev)
prev->next = temp;
// Set the previous node to the current
prev = temp;
currentLevelNodeCount--;
if (currentLevelNodeCount == 0) { // if this is the last node of the current level
currentLevelNodeCount = nextLevelNodeCount;
nextLevelNodeCount = 0;
prev = NULL;
}
Time Complexity: O(n). Space Complexity: O(n).
Problem-89 Can we improve space complexity for Problem-88?
Solution: We can process the tree level by level, but without a queue. The logical part is that when we process the nodes of the next level, we make sure that the current level has already been linked
void linkingNodesOfSame Level(struct BinaryTreeNode *root) {
if(!root) return;
struct BinaryTreeNode *rightMostNode = NULL, *nextHead = NULL, *temp = root;
//connect next level of current root node level
while(temp!= NULL){
if(temp-left!= NULL)
if(rightMostNode == NULL){
rightMostNode temp->left; nextHead-temp-left;
else{
rightMostNode->next = temp-left; rightMostNode rightMostNode-next;
if(temp-right!= NULL)
if(rightMostNode == NULL){
rightMostNode-temp-right;
nextHead-temp-right;
}
else{
rightMostNode->next = temp-right;
rightMostNode = rightMostNode->next;
}
temp-temp->next;
linkingNodesOfSame Level(nextHead);
Time Complexity: O(n). Space Complexity: O(depth of tree) for stack space.
Problem-90 Assume that a set S of n numbers are stored in some form of balanced binary search tree; i.e. the depth of the tree is O(logn). In addition to the key value and the pointers to children, assume that every node contains the number of nodes in its subtree. Specify a reason(s) why a balanced binary tree can be a better option than a complete binary tree for storing the set S.
Solution: Implementation of a balanced binary tree requires less RAM space as we do not need to keep the complete tree in RAM (since they use pointers).
Problem-91 For the Problem-90, specify a reason (s) why a complete binary tree can be a better option than a balanced binary tree for storing the set S.
Solution: A complete binary tree is more space efficient as we do not need any extra flags. A balanced binary tree usually takes more space since we need to store some flags. For example, in a Red-Black tree we need to store a bit for the color. Also, a complete binary tree can be stored in a RAM as an array without using pointers.
Problem-92 Given a binary tree, find the maximum path sum. The path may start and end at any node in the tree. Solution:
void linkingNodesOfSame Level(struct BinaryTreeNode *root) {
if(!root) return;
struct BinaryTreeNode *rightMostNode = NULL, *nextHead = NULL, *temp = root;
//connect next level of current root node level
while(temp!= NULL){
if(temp-left!= NULL)
if(rightMostNode == NULL){
rightMostNode temp->left; nextHead-temp-left;
else{
rightMostNode->next = temp-left; rightMostNode rightMostNode-next;
if(temp-right!= NULL)
if(rightMostNode == NULL){
rightMostNode-temp-right;
nextHead-temp-right;
}
else{
rightMostNode->next = temp-right;
rightMostNode = rightMostNode->next;
}
temp-temp->next;
linkingNodesOfSame Level(nextHead);
Problem-93 Let T be a proper binary tree with root r. Consider the following algorithm
int maxPathSum(struct Binary TreeNode *root){ int maxValue INT_MIN; return maxPathSumRec(root);
int max(int a, int b){ if (a>b) return a; else return b;
int maxPathSumRec(struct BinaryTreeNode *root) if (root == NULL) return 0;
int leftSum= maxPathSumRec(root-left); int rightSum maxPathSumRec(root-right);
if (leftSum < 0 && rightSum < 0){
maxValue = max(maxValue, root-data);
return root-data;
if (leftSum>0&& rightSum>0)
maxValue = max(maxValue, root-data + leftSum + rightSum);
maxValue Up = max(leftSum, rightSum) + root-data;
maxValue = max(maxValue, maxValue Up);
return maxValueUp;
What does the algorithm do?
A. It always returns the value 1.
B. It computes the number of nodes in the tree.
C. It computes the depth of the nodes.
D. It computes the height of the tree.
E. It computes the number of leaves in the tree.
Solution: E.
6.14 Other Variations on Trees
In this section, let us enumerate the other possible representations of trees. In the earlier sections, we have looked at AVL trees, which is a binary search tree (BST) with balancing property. Now, let us look at a few more balanced binary search trees: Red-black Trees and Splay Trees.
6.14.1 Red-Black Trees
In Red-black trees each node is associated with an extra attribute: the color, which is either red
or black. To get logarithmic complexity we impose the following restrictions.
Definition: A Red-black tree is a binary search tree that satisfies the following properties:
• Root Property: the root is black
• External Property: every leaf is black
• Internal Property: the children of a red node are black
• Depth Property: all the leaves have the same black
Similar to AVL trees, if the Red-black tree becomes imbalanced, then we perform rotations to reinforce the balancing property. With Red-black trees, we can perform the following operations in O(logn) in worst case, where n is the number of nodes in the trees.
• Insertion, Deletion
• Finding predecessor, successor
• Finding minimum, maximum
6.14.2 Splay Trees
Splay-trees are BSTs with a self-adjusting property. Another interesting property of splay-trees is: starting with an empty tree, any sequence of K operations with maximum of n nodes takes O(Klogn) time complexity in worst case. Splay trees are easier to program and also ensure faster access to recently accessed items. Similar to AVL and Red-Black trees, at any point that the splay tree becomes imbalanced, we can perform rotations to reinforce the balancing property.
Splay-trees cannot guarantee the O(logn) complexity in worst case. But it gives amortized O(logn) complexity. Even though individual operations can be expensive, any sequence of operations gets the complexity of logarithmic behavior. One operation may take more time (a single operation may take O(n) time) but the subsequent operations may not take worst case complexity and on the average per operation complexity is O{logn).
6.14.3 B-Trees
B-Tree is like other self-balancing trees such as AVL and Red-black tree such that it maintains its balance of nodes while opertions are performed against it. B-Tree has the following properties:
• Minimum degree “£” where, except root node, all other nodes must have no less than t – 1 keys
• Each node with n keys has n + 1 children
• Keys in each node are lined up where k1 < k2 < .. kn
• Each node cannot have more than 2t-l keys, thus 2t children
• Root node at least must contain one key. There is no root node if the tree is empty.
• Tree grows in depth only when root node is split.
Unlike a binary-tree, each node of a b-tree may have a variable number of keys and children. The keys are stored in non-decreasing order. Each key has an associated child that is the root of a subtree containing all nodes with keys less than or equal to the key but greater than the preceeding key. A node also has an additional rightmost child that is the root for a subtree containing all keys greater than any keys in the node.
A b-tree has a minumum number of allowable children for each node known as the minimization factor. If t is this minimization factor, every node must have at least t – 1 keys. Under certain circumstances, the root node is allowed to violate this property by having fewer than t – 1 keys.
Every node may have at most 2t – 1 keys or, equivalently, 2t children.
Since each node tends to have a large branching factor (a large number of children), it is typically neccessary to traverse relatively few nodes before locating the desired key. If access to each node requires a disk access, then a B-tree will minimize the number of disk accesses required. The
minimzation factor is usually chosen so that the total size of each node corresponds to a multiple of the block size of the underlying storage device. This choice simplifies and optimizes disk access. Consequently, a B-tree is an ideal data structure for situations where all data cannot reside in primary storage and accesses to secondary storage are comparatively expensive (or time consuming)
To search the tree, it is similar to binary tree except that the key is compared multiple times in a given node because the node contains more than 1 key. If the key is found in the node, the search terminates. Otherwise, it moves down where at child pointed by ci where key k < ki
Key insertions of a B-tree happens from the bottom fasion. This means that it walk down the tree from root to the target child node first. If the child is not full, the key is simply inserted. If it is full, the child node is split in the middle, the median key moves up to the parent, then the new key is inserted. When inserting and walking down the tree, if the root node is found to be full, it’s split first and we have a new root node. Then the normal insertion operation is performed.
Key deletion is more complicated as it needs to maintain the number of keys in each node to meet the constraint. If a key is found in leaf node and deleting it still keeps the number of keys in the nodes not too low, it’s simply done right away. If it’s done to the inner node, the predecessor of the key in the corresonding child node is moved to replace the key in the inner node. If moving the predecessor will cause the child node to violate the node count constraint, the sibling child nodes are combined and the key in the inner node is deleted.
6.14.4 Augmented Trees
In earlier sections, we have seen various problems like finding the K th – smallest – element in the tree and other similar ones. Of all the problems the worst complexity is O(n), where n is the number of nodes in the tree. To perform such operations in O(logn), augmented trees are useful. In
these trees, extra information is added to each node and that extra data depends on the problem we are trying to solve.
For example, to find the K th element in a binary search tree, let us see how augmented trees solve the problem. Let us assume that we are using Red-Black trees as balanced BST (or any balanced BST) and augmenting the size information in the nodes data. For a given node X in Red-Black tree with a field size(X) equal to the number of nodes in the subtree and can be calculated as:
size(X) = size(X → left) + size(X → right)) + 1
K th – smallest – operation can be defined as:
struct Binary SearcTreeNode *KthSmallest (struct BinarySearcTreeNode *X, int K) {
int r = size(X-left) + 1;
if(K == r)
return X;
if(Kr)
return KthSmallest (X-left, K);
if(Kr)
return KthSmallest (X-right, K-r);
Time Complexity: O(logn). Space Complexity: O(logn).
Example: With the extra size information, the augmented tree will look like
6.14.5 Interval Trees [Segment Trees]
We often face questions that involve queries made in an array based on range. For example, for a given array of integers, what is the maximum number in the range α to β, where α and β are of course within array limits. To iterate over those entries with intervals containing a particular value, we can use a simple array. But if we need more efficient access, we need a more sophisticated data structure.
An array-based storage scheme and a brute-force search through the entire array is acceptable only if a single search is to be performed, or if the number of elements is small. For example, if you know all the array values of interest in advance, you need to make only one pass through the array. However, if you can interactively specify different search operations at different times, the brute-force search becomes impractical because every element in the array must be examined during each search operation.
If you sort the array in ascending order of the array values, you can terminate the sequential search when you reach the object whose low value is greater than the element we are searching. Unfortunately, this technique becomes increasingly ineffective as the low value increases, because fewer search operations are eliminated. That means, what if we have to answer a large number of queries like this? – is brute force still a good option?
Another example is when we need to return a sum in a given range. We can brute force this too, but the problem for a large number of queries still remains. So, what can we do? With a bit of thinking we can come up with an approach like maintaining a separate array of n elements, where n is the size of the original array, where each index stores the sum of all elements from 0 to that index. So essentially we have with a bit of preprocessing brought down the query time from a worst case O(n) to O(1). Now this is great as far as static arrays are concerned, but, what if we are required to perform updates on the array too?
The first approach gives us an O(n) query time, but an O(1) update time. The second approach, on the other hand, gives us O(1) query time, but an O(n) update time. So, which one do we choose?
Interval trees are also binary search trees and they store interval information in the node structure. That means, we maintain a set of n intervals [i1 , i2 ] such that one of the intervals containing a query point Q (if any) can be found efficiently. Interval trees are used for performing range
queries efficiently.
A segment tree is a heap-like data structure that can be used for making update/query operations upon array intervals in logarithmical time. We define the segment tree for the interval [i,j] in the following recursive manner:
• The root (first node in the array) node will hold the information for the interval [i,j]
• If i < y the left and right children will hold the information for the intervals [i,i+1/2] and [i+j/2+1,j]
Segment trees (also called segtrees and interval trees) is a cool data structure, primarily used for range queries. It is a height balanced binary tree with a static structure. The nodes of a segment tree correspond to various intervals, and can be augmented with appropriate information pertaining to those intervals. It is somewhat less powerful than a balanced binary tree because of its static structure, but due to the recursive nature of operations on the segtree, it is incredibly easy to think about and code.
We can use segment trees to solve range minimum/maximum query problems. The time complexity is T(nlogn) where O(n) is the time required to build the tree and each query takes O(logn) time.
Example: Given a set of intervals: S= {[2-5], [6-7], [6-10], [8-9], [12-15], [15-23], [25-30]}. A query with Q = 9 returns [6,10] or [8,9] (assume these are the intervals which contain 9 among all the intervals). A query with Q = 23 returns [15, 23].
Construction of Interval Trees: Let us assume that we are given a set S of n intervals (called segments). These n intervals will have 2n endpoints. Now, let us see how to construct the interval tree.
Algorithm:
Recursively build tree on interval set 5 as follows:
• Sort the 2n endpoints
• Let Xmid be the median point
Time Complexity for building interval trees: O(nlogn). Since we are choosing the median, Interval Trees will be approximately balanced. This ensures that, we split the set of end points up in half each time. The depth of the tree is O(logn). To simplify the search process, generally Xmid is stored with each node.
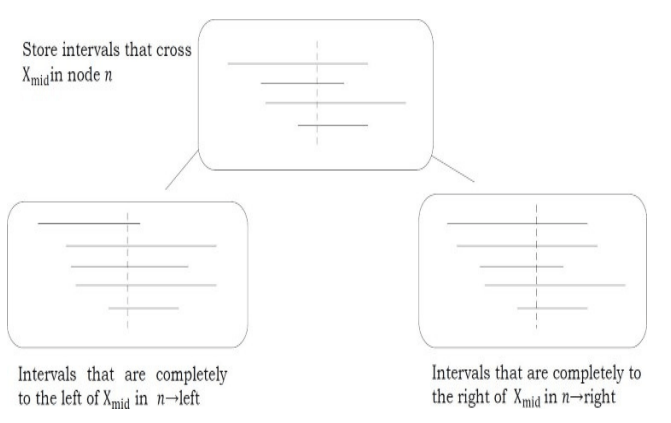
6.14.6 Scapegoat Trees
Scapegoat tree is a self-balancing binary search tree, discovered by Arne Andersson. It provides worst-case O(logn) search time, and O(logn) amortized (average) insertion and deletion time
AVL trees rebalance whenever the height of two sibling subtrees differ by more than one;
scapegoat trees rebalance whenever the size of a child exceeds a certain ratio of its parents, a ratio known as a. After inserting the element, we traverse back up the tree. If we find an imbalance where a child’s size exceeds the parent’s size times alpha, we must rebuild the subtree at the parent, the scapegoat.
There might be more than one possible scapegoat, but we only have to pick one. The most optimal scapegoat is actually determined by height balance. When removing it, we see if the total size of the tree is less than alpha of the largest size since the last rebuilding of the tree. If so, we rebuild the entire tree. The alpha for a scapegoat tree can be any number between 0.5 and 1.0. The value 0.5 will force perfect balance, while 1.0 will cause rebalancing to never occur, effectively turning it into a BST.

