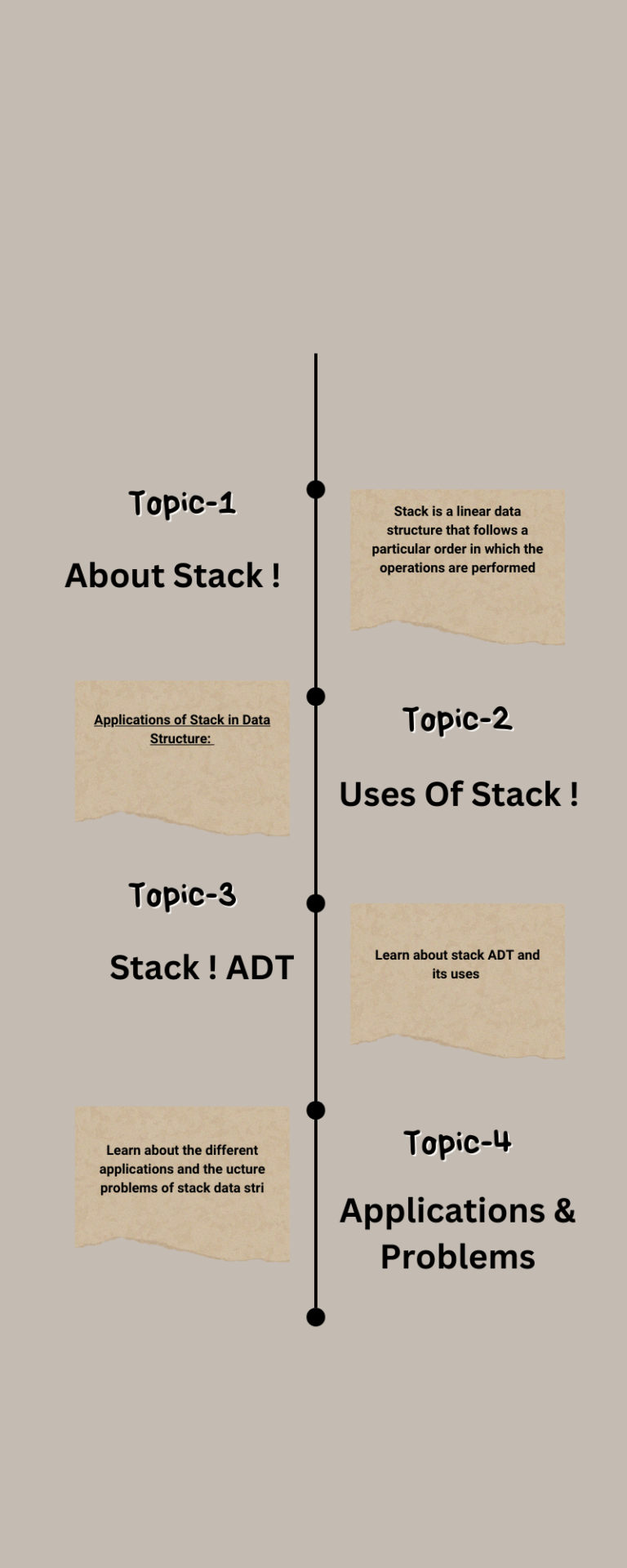
14.1 What is Hashing?
Hashing is a technique used for storing and retrieving information as quickly as possible. It is used to perform optimal searches and is useful in implementing symbol tables.
14.2 Why Hashing?
In the Trees chapter we saw that balanced binary search trees support operations such as insert, delete and search in O(logn) time. In applications, if we need these operations in O(1), then hashing provides a way. Remember that worst case complexity of hashing is still O(n), but it gives O(1) on the average.
14.3 HashTable ADT
The common operations for hash table are:
• CreatHashTable: Creates a new hash table
• HashSearch: Searches the key in hash table
• Hashlnsert: Inserts a new key into hash table
• HashDelete: Deletes a key from hash table
• DeleteHashTable: Deletes the hash table
14.4 Understanding Hashing
In simple terms we can treat array as a hash table. For understanding the use of hash tables, let us consider the following example: Give an algorithm for printing the first repeated character if there are duplicated elements in it. Let us think about the possible solutions. The simple and brute force way of solving is: given a string, for each character check whether that character is repeated or not. The time complexity of this approach is O(n 2 ) with O(1) space complexity.
Now, let us find a better solution for this problem. Since our objective is to find the first repeated character, what if we remember the previous characters in some array?
We know that the number of possible characters is 256 (for simplicity assume ASCII characters only). Create an array of size 256 and initialize it with all zeros. For each of the input characters go to the corresponding position and increment its count. Since we are using arrays, it takes constant time for reaching any location. While scanning the input, if we get a character whose counter is already 1 then we can say that the character is the one which is repeating for the first time.
char FirstRepeated Char (char *str) { int i, len=strlen(str);
int count[256]; //additional array for(i=0; i<256; ++i) count[i] = 0;
}
for(i=0; i<len; ++i) { if(count(str[i]]==1){ printf("%c", str[i]);
}
break;
else count(str[i]]++;
if(i==len)
printf("No Repeated Characters");
return 0;
Why not Arrays?
In the previous problem, we have used an array of size 256 because we know the number of different possible characters [256] in advance. Now, let us consider a slight variant of the same problem. Suppose the given array has numbers instead of characters, then how do we solve the problem?
14.12 Open Addressing
In open addressing all keys are stored in the hash table itself. This approach is also known as closed hashing. This procedure is based on probing. A collision is resolved by probing.
Linear Probing
The interval between probes is fixed at 1. In linear probing, we search the hash table sequentially, starting from the original hash location. If a location is occupied, we check the next location. We wrap around from the last table location to the first table location if necessary. The function for rehashing is the following:
rehash(key) = (n + 1)% tablesize
One of the problems with linear probing is that table items tend to cluster together in the hash table. This means that the table contains groups of consecutively occupied locations that are called clustering.
Clusters can get close to one another, and merge into a larger cluster. Thus, the one part of the table might be quite dense, even though another part has relatively few items. Clustering causes long probe searches and therefore decreases the overall efficiency.
The next location to be probed is determined by the step-size, where other step-sizes (more than one) are possible. The step-size should be relatively prime to the table size, i.e. their greatest common divisor should be equal to 1. If we choose the table size to be a prime number, then any step-size is relatively prime to the table size. Clustering cannot be avoided by larger step-sizes.
Quadratic Probing
The interval between probes increases proportionally to the hash value (the interval thus increasing linearly, and the indices are described by a quadratic function). The problem of Clustering can be eliminated if we use the quadratic probing method.
In quadratic probing, we start from the original hash location i. If a location is occupied, we check the locations i + 1 2 , i +2 2 , i + 3 2 , i + 4 2 … We wrap around from the last table location to the first table location if necessary. The function for rehashing is the following:
rehash(key) = (n + k2)% tablesize
Example: Let us assume that the table size is 11 (0..10)
Hash Function: h(key) = key mod 11

Insert keys
31 mod 11 = 9
19 mod 11 = 8
2 mod 11 = 2
13 mod 11 = 2 → 2 + 1 2 = 3
25 mod 11 = 3 → 3 + 1 2=4
24 mod 11 = 2 → 2 + 1 2 , 2 + 2 2 = 6
21 mod 11 = 10
9 mod 11 = 9 → 9 + 1 2 , 9 + 2
2 mod 11, 9 + 3
2 mod 11=7
Even though clustering is avoided by quadratic probing, still there are chances of clustering. Clustering is caused by multiple search keys mapped to the same hash key. Thus, the probing sequence for such search keys is prolonged by repeated conflicts along the probing sequence. Both linear and quadratic probing use a probing sequence that is independent of the search key.
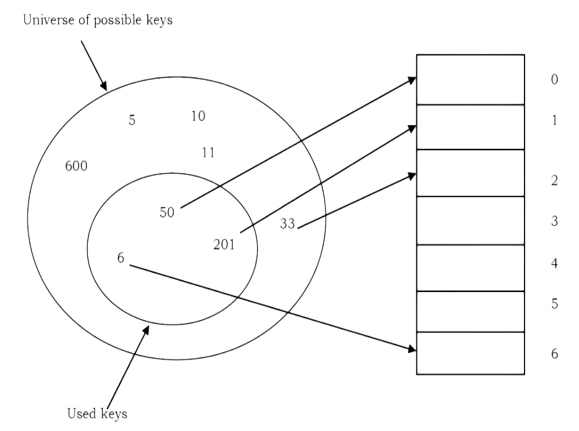
Double Hashing
The interval between probes is computed by another hash function. Double hashing reduces clustering in a better way. The increments for the probing sequence are computed by using a second hash function. The second hash function h2 should be:
h2(key) ≠ 0 and h2 ≠ h1
We first probe the location h1(key). If the location is occupied, we probe the location h1(key) +
h2(key), h1(key) + 2 * h2(key), …
Example:
Table size is 11 (0..10)
Hash Function: assume h1(key) = key mod 11 and h2(key) = 7- (key mod 7)
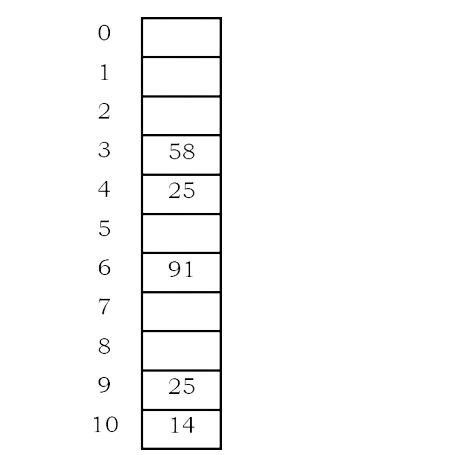
Insert keys:
58 mod 11 = 3
14 mod 11 = 3 → 3 + 7 = 10
91 mod 11 = 3 → 3+ 7,3+ 2*
7 mod 11 = 6
25 mod 11 = 3 → 3 + 3,3 + 2*3 = 9
14.13 Comparison of Collision Resolution Techniques
Comparisons: Linear Probing vs. Double Hashing
The choice between linear probing and double hashing depends on the cost of computing the hash function and on the load factor [number of elements per slot] of the table. Both use few probes but double hashing take more time because it hashes to compare two hash functions for long keys.
Comparisons: Open Addressing vs. Separate Chaining
It is somewhat complicated because we have to account for the memory usage. Separate chaining uses extra memory for links. Open addressing needs extra memory implicitly within the table to terminate the probe sequence. Open-addressed hash tables cannot be used if the data does not have unique keys. An alternative is to use separate chained hash tables.
Comparisons: Open Addressing methods

14.14 How Hashing Gets O(1) Complexity
From the previous discussion, one doubts how hashing gets O(1) if multiple elements map to the same location…
The answer to this problem is simple. By using the load factor we make sure that each block (for example, linked list in separate chaining approach) on the average stores the maximum number of elements less than the load factor. Also, in practice this load factor is a constant (generally, 10 or 20). As a result, searching in 20 elements or 10 elements becomes constant.
If the average number of elements in a block is greater than the load factor, we rehash the elements with a bigger hash table size. One thing we should remember is that we consider average occupancy (total number of elements in the hash table divided by table size) when deciding the rehash.
The access time of the table depends on the load factor which in turn depends on the hash function. This is because hash function distributes the elements to the hash table. For this reason, we say hash table gives O(1) complexity on average. Also, we generally use hash tables in cases where searches are more than insertion and deletion operations.
14.15 Hashing Techniques
There are two types of hashing techniques:
static hashing and dynamic hashing
Static Hashing If the data is fixed then static hashing is useful. In static hashing, the set of keys is kept fixed and given in advance, and the number of primary pages in the directory are kept fixed.
Dynamic Hashing
If the data is not fixed, static hashing can give bad performance, in which case dynamic hashing is the alternative, in which case the set of keys can change dynamically.
14.16 Problems for which Hash Tables are not suitable
• Problems for which data ordering is required
• Problems having multidimensional data
• Prefix searching, especially if the keys are long and of variable-lengths
• Problems that have dynamic data
• Problems in which the data does not have unique keys.
14.17 Bloom Filters
A Bloom filter is a probabilistic data structure which was designed to check whether an element is present in a set with memory and time efficiency. It tells us that the element either definitely is not in the set or may be in the set. The base data structure of a Bloom filter is a Bit Vector. The algorithm was invented in 1970 by Burton Bloom and it relies on the use of a number of different hash functions.
How it works?

Now that the bits in the bit vector have been set for Element1 and Element2; we can query the bloom filter to tell us if something has been seen before.
The element is hashed but instead of setting the bits, this time a check is done and if the bits that would have been set are already set the bloom filter will return true that the element has been seen before.
A Bloom filter starts off with a bit array initialized to zero. To store a data value, we simply apply k different hash functions and treat the resulting k values as indices in the array, and we set each of the k array elements to 1. We repeat this for every element that we encounter.
Now suppose an element turns up and we want to know if we have seen it before. What we do is apply the k hash functions and look up the indicated array elements. If any of them are 0 we can be 100% sure that we have never encountered the element before – if we had, the bit would have been set to 1. However, even if all of them are one, we still can’t conclude that we have seen the element before because all of the bits could have been set by the k hash functions applied to multiple other elements. All we can conclude is that it is likely that we have encountered the element before.
Note that it is not possible to remove an element from a Bloom filter. The reason is simply that we can’t unset a bit that appears to belong to an element because it might also be set by another element.
If the bit array is mostly empty, i.e., set to zero, and the k hash functions are independent of one another, then the probability of a false positive (i.e., concluding that we have seen a data item when we actually haven’t) is low. For example, if there are only k bits set, we can conclude that the probability of a false positive is very close to zero as the only possibility of error is that we entered a data item that produced the same k hash values – which is unlikely as long as the ‘has’ functions are independent.
As the bit array fills up, the probability of a false positive slowly increases. Of course when the bit array is full, every element queried is identified as having been seen before. So clearly we can trade space for accuracy as well as for time.
One-time removal of an element from a Bloom filter can be simulated by having a second Bloom filter that contains elements that have been removed. However, false positives in the second filter become false negatives in the composite filter, which may be undesirable. In this approach, readding a previously removed item is not possible, as one would have to remove it from the removed filter.
Selecting hash functions
The requirement of designing k different independent hash functions can be prohibitive for large k. For a good hash function with a wide output, there should be little if any correlation between different bit-fields of such a hash, so this type of hash can be used to generate multiple different hash functions by slicing its output into multiple bit fields. Alternatively, one can pass k different initial values (such as 0, 1, …, k – 1) to a hash function that takes an initial value – or add (or append) these values to the key. For larger m and/or k, independence among the hash functions can be relaxed with negligible increase in the false positive rate.
Selecting size of bit vector
A Bloom filter with 1% error and an optimal value of k, in contrast, requires only about 9.6 bits per element – regardless of the size of the elements. This advantage comes partly from its compactness, inherited from arrays, and partly from its probabilistic nature. The 1% falsepositive rate can be reduced by a factor of ten by adding only about 4.8 bits per element.
Space Advantages
While risking false positives, Bloom filters have a strong space advantage over other data structures for representing sets, such as self-balancing binary search trees, tries, hash tables, or simple arrays or linked lists of the entries. Most of these require storing at least the data items themselves, which can require anywhere from a small number of bits, for small integers, to an arbitrary number of bits, such as for strings (tries are an exception, since they can share storage between elements with equal prefixes). Linked structures incur an additional linear space overhead for pointers.
However, if the number of potential values is small and many of them can be in the set, the Bloom filter is easily surpassed by the deterministic bit array, which requires only one bit for each potential element.
Time Advantages
Bloom filters also have the unusual property that the time needed either to add items or to check whether an item is in the set is a fixed constant, O(k), completely independent of the number of items already in the set. No other constant-space set data structure has this property, but the average access time of sparse hash tables can make them faster in practice than some Bloom filters. In a hardware implementation, however, the Bloom filter shines because its k lookups are independent and can be parallelized.
Implementation
Refer to Problems Section.
14.18 Hashing: Problems & Solutions
Problem-1 Implement a separate chaining collision resolution technique. Also, discuss time complexities of each function.
Solution: To create a hashtable of given size, say n, we allocate an array of n/L (whose value is usually between 5 and 20) pointers to list, initialized to NULL. To perform Search/Insert/Delete operations, we first compute the index of the table from the given key by using hashfunction and then do the corresponding operation in the linear list maintained at that location. To get uniform distribution of keys over a hashtable, maintain table size as the prime number
#define LOAD_FACTOR 20 struct ListNode {
}
int key;
int data;
struct ListNode "next;
struct HashTableNode{ int bcount;
//Number of elements in block
struct ListNode *next;
int tsize;
int count;
struct HashTable {
//Number of elements in table
struct HashTableNode **Table;
struct HashTable "CreatHashTable(int size) {
struct HashTable "h;
h = (struct HashTable *)malloc(sizeof(struct HashTable));
if(th)
return NULL;
h-tsize-size/ LOAD_FACTOR;
h-count=0;
h-Table = (struct HashTableNode **)malloc(sizeof(struct HashTableNode *) * h→→tsize); if(!h-Table) {
}
}
}
printf("Memory Error");
return NULL;
for(int i=0; i < h-tsize; i++) {
h-Table[i]-next = NULL;
h-Table[i]-bcount = 0;
return h;
int HashSearch(Struct HashTable 'h, int data) {
struct ListNode "temp;
temp-h-Table[Hash(data, h-tsize)]-next; while(temp) {
}
return 0;
if(temp-data data)
return 1;
temp-temp->next;
int HashInsert(Struct HashTable "h, int data) {
int index;
struct ListNode "temp, 'newNode;
if(HashSearch(h, data))
return 0;
index= Hash(data, h-tsize);
temp-h-Table[index]-next;
//Assume Hash is a built-in function
//Assume Hash is a built-in function
newNode = (struct ListNode *)malloc(sizeof(struct ListNode));
if(!newNode) {
printf("Out of Space");
return -1;
newNode-key index;
newNode-data = data;
newNode-next-h-Table/index]-next:
h-Table[index]-next = newNode; h-Table[index]-bcount++;
h-count++;
if(h-count/h-tsize > LOAD_FACTOR) Rehash(h);
return 1;
int HashDelete(Struct HashTable "h, int data) {
int index;
struct ListNode *temp, "prev;
index Hash(data, h-tsize);
for(temp-h-Table[index]-next, prev = NULL; temp; prev = temp, temp = temp->next) { if(temp-data == data) { if(prev!= NULL)
prev next temp->next;
free(temp);
h-Table[index]-bcount--;
}
h-count--;
return 1;
return 0;
void Rehash(Struct HashTable *h) {
int oldsize, i, index;
}
struct ListNode *p, temp, *temp2;
struct HashTableNode **oldTable; oldsize=h-tsize;
old Table - h-Table;
h-tsize = h-tsize*2;
h-Table = (struct HashTableNode **)malloc(h-tsize* sizeof(struct HashTableNode *));
if(!h-Table) {
printf("Allocation Failed");
return;
for(i = 0; i < oldsize; i++) {
for(temp = oldTable[i]-next; temp; temp = temp→next) {
index = Hash(temp-data, h-tsize);
temp2 = temp; temp = temp->next;
temp2-next-h-Table[index]-next; h-Table[index]-next = temp2;
CreatHashTable – O(n). HashSearch – O(1) average. Hashlnsert – O(1) average. HashDelete – O(1) average.
Problem-2 Given an array of characters, give an algorithm for removing the duplicates.
Solution: Start with the first character and check whether it appears in the remaining part of the string using a simple linear search. If it repeats, bring the last character to that position and decrement the size of the string by one. Continue this process for each distinct character of the given string.
int elem(int *A, size_t n, int e){ for (int i = 0; i < n; ++i)
}
if (A[i]
e)
return 1;
return 0;
int RemoveDuplicates (int *A, int n){
int m = 0;
for (int i = 0; i < n; ++i) if (lelem(A, m, A[i])) A[m++] = A[i];
return m;
Time Complexity: O(n 2 ). Space Complexity: O(1).
Problem-3 Can we find any other idea to solve this problem in better time than O(n 2 )? Observe that the order of characters in solutions do not matter.
Solution: Use sorting to bring the repeated characters together. Finally scan through the array to remove duplicates in consecutive positions
int Compare(const void* a, const void *b) { return *(char*)a (char*)b;
}
void Remove Duplicates(char s[]) {
int last, current;
QuickSort(s, strlen(s), sizeof(char), Compare); current = 0, last = 0;
for(; s[current]; i++) {
if(s[last]!= s[current]) s++last] s[current];
s[last]='\0';
Time Complexity: Θ(nlogn). Space Complexity: O(1).
Problem-4 Can we solve this problem in a single pass over given array?
Solution: We can use hash table to check whether a character is repeating in the given string or not. If the current character is not available in hash table, then insert it into hash table and keep that character in the given string also. If the current character exists in the hash table then skip that character.
void Remove Duplicates (char s[]) { int src, dst;
struct Hast Table *h; h = CreatHashTable(); current = last = 0;
for(; s[current]; current++) {
if( !HashSearch(h, s[current])) { s[last++] = s[current]; Hashinsert(h, s[current]);
}
s[last] = '\0';
Time Complexity: Θ(n) on average. Space Complexity: O(n).
Problem-5 Given two arrays of unordered numbers, check whether both arrays have the same set of numbers?
Solution: Let us assume that two given arrays are A and B. A simple solution to the given problem is: for each element of A, check whether that element is in B or not. A problem arises with this approach if there are duplicates. For example consider the following inputs:
A = {2,5,6,8,10,2,2}
B = {2,5,5,8,10,5,6}
The above algorithm gives the wrong result because for each element of A there is an element in B also. But if we look at the number of occurrences, they are not the same. This problem we can solve by moving the elements which are already compared to the end of the list. That means, if we find an element in B, then we move that element to the end of B, and in the next searching we will not find those elements. But the disadvantage of this is it needs extra swaps. Time Complexity of this approach is O(n 2 ), since for each element of A we have to scan B.
Problem-6 Can we improve the time complexity of Problem-5?
Solution: Yes. To improve the time complexity, let us assume that we have sorted both the lists. Since the sizes of both arrays are n, we need O(n log n) time for sorting them. After sorting, we just need to scan both the arrays with two pointers and see whether they point to the same element every time, and keep moving the pointers until we reach the end of the arrays.
Time Complexity of this approach is O(n log n). This is because we need O(n log n) for sorting the arrays. After sorting, we need O(n) time for scanning but it is less compared to O(n log n).
Problem-7 Can we further improve the time complexity of Problem-5?
Solution: Yes, by using a hash table. For this, consider the following algorithm. Algorithm:
• Construct the hash table with array A elements as keys.
• While inserting the elements, keep track of the number frequency for each number. That means, if there are duplicates, then increment the counter of that corresponding key.
• After constructing the hash table for A’s elements, now scan the array B.
• For each occurrence of B’s elements reduce the corresponding counter values.
• At the end, check whether all counters are zero or not.
• If all counters are zero, then both arrays are the same otherwise the arrays are different.
Time Complexity; O(n) for scanning the arrays. Space Complexity; O(n) for hash table.
Problem-8 Given a list of number pairs; if pair(i,j) exists, and pair(j,i) exists, report all such pairs. For example, in {{1,3},{2,6},{3,5},{7,4},{5,3},{8,7}}, we see that {3,5} and {5,3} are present. Report this pair when you encounter {5,3}. We call such pairs ‘symmetric pairs’. So, give an efficient algorithm for finding all such pairs.
Solution: By using hashing, we can solve this problem in just one scan. Consider the following algorithm. Algorithm:
• Read the pairs of elements one by one and insert them into the hash table. For each pair, consider the first element as key and the second element as value.
• While inserting the elements, check if the hashing of the second element of the current pair is the same as the first number of the current pair.
• If they are the same, then that indicates a symmetric pair exits and output that pair.
• Otherwise, insert that element into that. That means, use the first number of the current pair as key and the second number as value and insert them into the hash table.
• By the time we complete the scanning of all pairs, we have output all the symmetric pairs.
Time Complexity; O(n) for scanning the arrays. Note that we are doing a scan only of the input. Space Complexity; O(n) for hash table.
Problem-9 Given a singly linked list, check whether it has a loop in it or not.
Solution: Using Hash Tables
Algorithm:
• Traverse the linked list nodes one by one.
• Check if the node’s address is there in the hash table or not.
• If it is already there in the hash table, that indicates we are visiting a node which was already visited. This is possible only if the given linked list has a loop in it.
• If the address of the node is not there in the hash table, then insert that node’s address into the hash table.
• Continue this process until we reach the end of the linked list or we find the loop.
Time Complexity; O(n) for scanning the linked list. Note that we are doing a scan only of the input. Space Complexity; O(n) for hash table.
Note: for an efficient solution, refer to the Linked Lists chapter.
Problem-10 Given an array of 101 elements. Out of them 50 elements are distinct, 24 elements are repeated 2 times, and one element is repeated 3 times. Find the element that is repeated 3 times in O(1).
Solution: Using Hash Tables
Algorithm:
• Scan the input array one by one.
• Check if the element is already there in the hash table or not.
• If it is already there in the hash table, increment its counter value [this indicates the number of occurrences of the element].
• If the element is not there in the hash table, insert that node into the hash table with counter value 1.
• Continue this process until reaching the end of the array.
Time Complexity: O(n), because we are doing two scans. Space Complexity: O(n), for hash table.
Note: For an efficient solution refer to the Searching chapter.
Problem-11 Given m sets of integers that have n elements in them, provide an algorithm to find an element which appeared in the maximum number of sets?
Solution: Using Hash Tables
Algorithm:
• Scan the input sets one by one.
• For each element keep track of the counter. The counter indicates the frequency of occurrences in all the sets.
• After completing the scan of all the sets, select the one which has the maximum counter value.
Time Complexity: O(mn), because we need to scan all the sets. Space Complexity: O(mn), for hash table. Because, in the worst case all the elements may be different.
Problem-12 Given two sets A and B, and a number K, Give an algorithm for finding whether there exists a pair of elements, one from A and one from B, that add up to K.
Solution: For simplicity, let us assume that the size of A is m and the size of B is n.
Algorithm:
• Select the set which has minimum elements.
• For the selected set create a hash table. We can use both key and value as the same.
• Now scan the second array and check whether (K-selected element) exists in the hash table or not.
• If it exists then return the pair of elements.
• Otherwise continue until we reach the end of the set.
Time Complexity: O(Max(m,n)), because we are doing two scans. Space Complexity: O(Min(m,n)), for hash table. We can select the small set for creating the hash table.
Problem-13 Give an algorithm to remove the specified characters from a given string which are given in another string?
Solution: For simplicity, let us assume that the maximum number of different characters is 256. First we create an auxiliary array initialized to 0. Scan the characters to be removed, and for each of those characters we set the value to 1, which indicates that we need to remove that character.
After initialization, scan the input string, and for each of the characters, we check whether that character needs to be deleted or not. If the flag is set then we simply skip to the next character, otherwise we keep the character in the input string. Continue this process until we reach the end of the input string. All these operations we can do in-place as given below.
void RemoveChars(char str[], char remove TheseChars[]) {
int srcind, destind;
int auxi[256]; //additional array for(srcInd=0; srcInd<256; srcIndex++) auxi[srcInd]=0;
}
//set true for all characters to be removed srcIndex=0;
while(remove TheseChars[srcInd]) {
auxi[remove TheseChars[srcInd]]=1; srclnd++;
//copy chars unless it must be removed
srclnd-destind=0;
while(str[srcInd++]) {
if(lauxi[str[srclnd]])
str[destind++]=str[srcInd];
}
Time Complexity: Time for scanning the characters to be removed + Time for scanning the input array= O(n) +O(m) ≈ O(n). Where m is the length of the characters to be removed and n is the length of the input string.
Space Complexity: O(m), length of the characters to be removed. But since we are assuming the maximum number of different characters is 256, we can treat this as a constant. But we should keep in mind that when we are dealing with multi-byte characters, the total number of different characters is much more than 256.
Problem-14 Give an algorithm for finding the first non-repeated character in a string. For example, the first non-repeated character in the string “abzddab” is ‘z’.
Solution: The solution to this problem is trivial. For each character in the given string, we can scan the remaining string if that character appears in it. If it does not appears then we are done with the solution and we return that character. If the character appears in the remaining string, then go to the next character.
char First Non Repeated Char( char *str) { int i, j, repeated = 0; int len = strlen(str); for(i=0; i<len; i++) { repeated = 0;
for(j=0; j < len; j++) { if(i!= j && str[i]== str[j]) {
}
}
if repeated == 0)
repeated = 1; break;
return str[i];
// Found the first non-repeated character
return
Time Complexity: O(n 2 ), for two for loops. Space Complexity: O(1).
Problem-15 Can we improve the time complexity of Problem-13?
Solution: Yes. By using hash tables we can reduce the time complexity. Create a hash table by reading all the characters in the input string and keeping count of the number of times each character appears. After creating the hash table, we can read the hash table entries to see which element has a count equal to 1. This approach takes O(n) space but reduces the time complexity also to O(n)
char First Non Repeated CharUsinghash(char *str) { int i, len-strlen(str);
int count[256]; //additional array for(i=0;i<len; ++i) count[i] = 0;
for(i=0;i<len; ++i) count(str[i]]++;
for(i=0; i<len; ++i) {
if(count(str[i]]==1){
printf("%c", str[i]);
break;
}
if(i==len)
printf("No Non-repeated Characters");
return 0;
Time Complexity; We have O(n) to create the hash table and another O(n) to read the entries of hash table. So the total time is O(n) + O(n) = O(2n) ≈ O(n). Space Complexity: O(n) for keeping the count values.
Problem-16 Given a string, give an algorithm for finding the first repeating letter in a string?
Solution: The solution to this problem is somewhat similar to Problem-13 and Problem-15. The only difference is, instead of scanning the hash table twice we can give the answer in just one scan. This is because while inserting into the hash table we can see whether that element already exists or not. If it already exists then we just need to return that character.
char First
RepeatedCharUsinghash(char *str) {
int i, len-strlen(str);
int count[256]; //additional array for(i=0;i<len; ++i) count[i] = 0; for(i=0; i<len; ++i) { if(count(str[i]]==1) { printf("%s", str[i]);
}
}
break;
else count(str[i]]++;
if(i==len)
printf("No Repeated Characters");
return 0;
Time Complexity: We have O(n) for scanning and creating the hash table. Note that we need only one scan for this problem. So the total time is O(n). Space Complexity: O(n) for keeping the count values.
Problem-17 Given an array of n numbers, create an algorithm which displays all pairs whose sum is S.
Solution: This problem is similar to Problem-12. But instead of using two sets we use only one set.
Algorithm:
• Scan the elements of the input array one by one and create a hash table. Both key and value can be the same.
• After creating the hash table, again scan the input array and check whether (S – selected element) exits in the hash table or not.
• If it exits then return the pair of elements.
• Otherwise continue and read all the elements of the array.
Time Complexity; We have O(n) to create the hash table and another O(n) to read the entries of the hash table. So the total time is O(n) + O(n) = O(2n) ≈ O(n). Space Complexity: O(n) for keeping the count values.
Problem-18 Is there any other way of solving Problem-17?
Solution: Yes. The alternative solution to this problem involves sorting. First sort the input array. After sorting, use two pointers, one at the starting and another at the ending. Each time add the values of both the indexes and see if their sum is equal to S. If they are equal then print that pair. Otherwise increase the left pointer if the sum is less than S and decrease the right pointer if the sum is greater than S.
Time Complexity: Time for sorting + Time for scanning = O(nlogn) + O(n) ≈ O(nlogn). Space Complexity: O(1).
Problem-19 We have a file with millions of lines of data. Only two lines are identical; the rest are unique. Each line is so long that it may not even fit in the memory. What is the most efficient solution for finding the identical lines?
Solution: Since a complete line may not fit into the main memory, read the line partially and compute the hash from that partial line. Then read the next part of the line and compute the hash. This time use the previous hash also while computing the new hash value. Continue this process until we find the hash for the complete line. Do this for each line and store all the hash values in a file [or maintain a hash table of these hashes]. If at any point you get same hash value, read the corresponding lines part by part and compare.
Note: Refer to Searching chapter for related problems.
Problem-20 If h is the hashing function and is used to hash n keys into a table of size s, where n <= s, the expected number of collisions involving a particular key X is :
(A) less than 1.
(B) less than n.
(C) less than s.
(D) less than n/2 .
Solution: A.
Problem-21 Implement Bloom Filters
Solution: A Bloom Filter is a data structure designed to tell, rapidly and memory-efficiently, whether an element is present in a set. It is based on a probabilistic mechanism where false positive retrieval results are possible, but false negatives are not. At the end we will see how to tune the parameters in order to minimize the number of false positive results.
Let’s begin with a little bit of theory. The idea behind the Bloom filter is to allocate a bit vector of length m, initially all set to 0, and then choose k independent hash functions, h1 , h2 , …, hk , each with range [1..m]. When an element a is added to the set then the bits at positions h1 (a), h2 (a), …, hk (a) in the bit vector are set to 1. Given a query element q we can test whether it is in the set using the bits at positions h1 (q), h2 (q), …, hk (q) in the vector. If any of these bits is 0 we report that q is not in the set otherwise we report that q is. The thing we have to care about is that in the first case there remains some probability that q is not in the set which could lead us to a false positive response.
typedef unsigned int ("hashFunction Pointer)(const char *);
struct Bloom
int bloomArraySize:
unsigned char *bloomArray; int nHashFunctions;
hashFunctionPointer *funcsArray:
#define SETBLOOMBIT(a, n) (a/n/CHAR_BIT] - (1<< (n%CHAR_BIT))) #define GETBLOOMBIT(a, n) (aln/CHAR_BIT] & (1<< (n%CHAR_BIT)))
struct Bloom *createBloom(int size, int nHashFunctions,...){
struct Bloom *blm;
va_list 1;
int n;
if(!(blm-malloc(sizeof(struct Bloom))))
return NULL;
if(blm-bloomArray-calloc((size+CHAR_BIT-1)/CHAR_BIT, sizeof(char)))) {
}
free(blm):
return NULL;
if(blm-funesArray-(hashFunctionPointer*)malloc(nHashFunctions* sizeof(hashFunctionPointer)))) {
free(blm-bloomArray):
free(blm);
return NULL;
va_start(1, nHashFunctions);
for(n-0; nenHashFunctions; ++n) {
}
blm-funcsArray[n]-va_arg(l, hashFunctionPointer);
va_end(1);
blm-nHashFunctions-nHash Functions; blm-bloomArraySize-size;
return blm;
int deleteBloom(struct Bloom "blm){
}
free(blm-bloomArray); free blm-funcsArray); free(blm);
return 0;
int addElementBloom(struct Bloom *blm, const char *s){
for(int n-0; n<blm-nHashFunctions; ++) {
SETBLOOMBIT(blm-bloomArray, blm-funcsArray[n](s)% blm-bloomArraySize);
return 0;
int checkElementBloom(struct Bloom *blm, const char *s){
}
for(int n=0; n<blm-nHashFunctions; ++n) {
if((GETBLOOMBIT (blm-bloomArray, blm-funcsArray[n] (s) % blm-bloomArraySize))) return 0;
return 1;
unsigned int shiftAddXORHash(const char *key){
1
unsigned int h=0;
while('key) h^=(h<<5)+(h>>2)+(unsigned char)*key++; return h;
unsigned int XORHash(const char *key){
unsigned int h=0;
hash_th-0;
while("key) h^*key++; return h;
int test(){ FILE *fp; char line[1024];
char *p;
struct Bloom *blm;
if(!(blm-createBloom (1500000, 2, shiftAddXORHash, XORHash))) { fprintf(stderr, "ERROR: Could not create Bloom filter\n");
}
return -1;
if(!(fp-fopen("path", "r")){
}
fprintf(stderr, "ERROR: Could not open file %s\n", argv[1]); return -1;
while(fgets(line, 1024, fp)) {
if((p-strchr(line, '\r'])) *p='\0';
if((p=strchr(line, '\n'))) "p='\0';
addElement Bloom(blm, line);
}
fclose(fp);
while(fgets(line, 1024, stdin)) {
if((p=strchr(line, '\r'))) *p='\0';
if((p=strchr(line, '\n'))) "p='\0';
p=strtok(line, "\t,.;:\r\n?!-/0");
while(p) {
}
}
}
if(!checkBloom(blm, p)) {
printf("No match for ford \"%s\"\n", p);
p=strtok(NULL, " \t,.;:\r\n?!-/0");
deleteBloom(blm);
return 1;

