7.1 What is a Priority Queue?
In some situations we may need to find the minimum/maximum element among a collection of elements. We can do this with the help of Priority Queue ADT. A priority queue ADT is a data structure that supports the operations Insert and DeleteMin (which returns and removes the minimum element) or DeleteMax (which returns and removes the maximum element).
These operations are equivalent to EnQueue and DeQueue operations of a queue. The difference is that, in priority queues, the order in which the elements enter the queue may not be the same in which they were processed. An example application of a priority queue is job scheduling, which is prioritized instead of serving in first come first serve.

A priority queue is called an ascending – priority queue, if the item with the smallest key has the highest priority (that means, delete the smallest element always). Similarly, a priority queue is said to be a descending –priority queue if the item with the largest key has the highest priority (delete the maximum element always). Since these two types are symmetric we will be concentrating on one of them: ascending-priority queue.
7.2 Priority Queue ADT
The following operations make priority queues an ADT
Main Priority Queues Operations
A priority queue is a container of elements, each having an associated key.
• Insert (key, data): Inserts data with key to the priority queue. Elements are ordered based on key.
• DeleteMin/DeleteMax: Remove and return the element with the smallest/largest key.
• GetMinimum/GetMaximum: Return the element with the smallest/largest key without deleting it.
Auxiliary Priority Queues Operations
• k th – Smallest/k th – Largest: Returns the k th -Smallest/k th –Largest key in priority queue.
• Size: Returns number of elements in priority queue.
• Heap Sort: Sorts the elements in the priority queue based on priority (key).
7.3 Priority Queue Applications
Priority queues have many applications – a few of them are listed below:
• Data compression: Huffman Coding algorithm
• Shortest path algorithms: Dijkstra’s algorithm
• Minimum spanning tree algorithms: Prim’s algorithm
• Event-driven simulation: customers in a line
• Selection problem: Finding k th – smallest element
7.4 Priority Queue Implementations
Before discussing the actual implementation, let us enumerate the possible options.
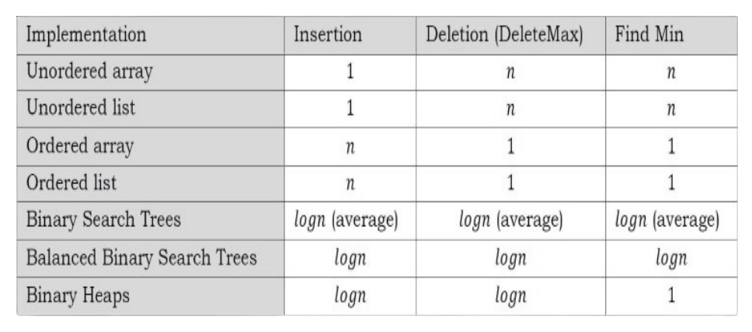
Unordered Array Implementation
Elements are inserted into the array without bothering about the order. Deletions (DeleteMax) are performed by searching the key and then deleting.
Insertions complexity: O(1). DeleteMin complexity: O(n).
Unordered List Implementation
It is very similar to array implementation, but instead of using arrays, linked lists are used.
Insertions complexity: O(1). DeleteMin complexity: O(n).
Ordered Array Implementation
Elements are inserted into the array in sorted order based on key field. Deletions are performed at only one end.
Insertions complexity: O(n). DeleteMin complexity: O(1).
Ordered List Implementation
Elements are inserted into the list in sorted order based on key field. Deletions are performed at only one end, hence preserving the status of the priority queue. All other functionalities associated with a linked list ADT are performed without modification.
Insertions complexity: O(n). DeleteMin complexity: O(1).
Binary Search Trees Implementation
Both insertions and deletions take O(logn) on average if insertions are random (refer to Trees chapter).
Balanced Binary Search Trees Implementation
Both insertions and deletion take O(logn) in the worst case (refer to Trees chapter).
Binary Heap Implementation
In subsequent sections we will discuss this in full detail. For now, assume that binary heap implementation gives O(logn) complexity for search, insertions and deletions and O(1) for finding the maximum or minimum element.
Comparing Implementations
7.5 Heaps and Binary Heaps
What is a Heap?
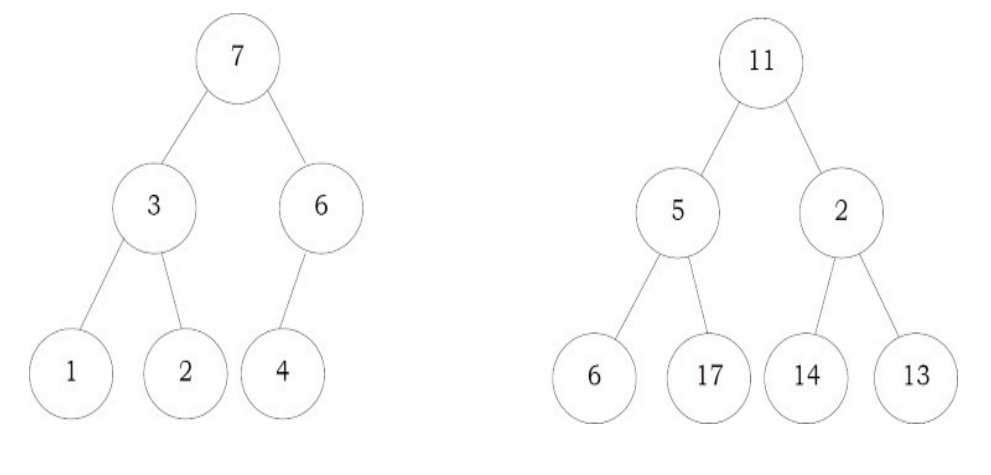
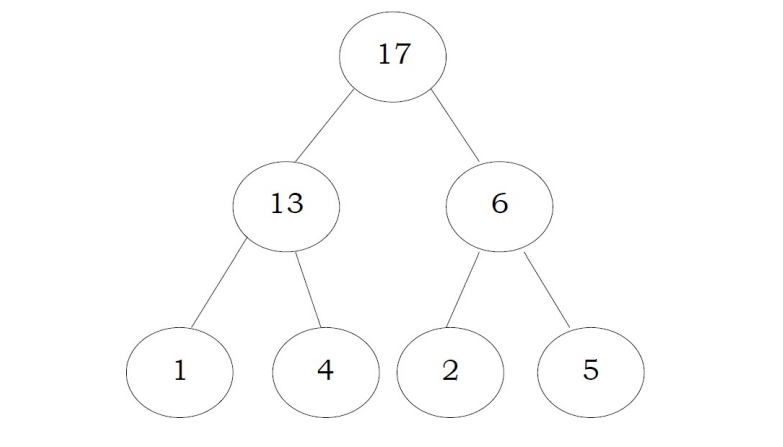
A heap is a tree with some special properties. The basic requirement of a heap is that the value of a node must be ≥ (or ≤) than the values of its children. This is called heap property. A heap also has the additional property that all leaves should be at h or h – 1 levels (where h is the height of the tree) for some h > 0 (complete binary trees). That means heap should form a complete binary tree (as shown below).

In the examples below, the left tree is a heap (each element is greater than its children) and the right tree is not a heap (since 11 is greater than 2)
Types of Heaps?
Based on the property of a heap we can classify heaps into two types:
• Min heap: The value of a node must be less than or equal to the values of its children

• Max heap: The value of a node must be greater than or equal to the values of its children
7.6 Binary Heaps
In binary heap each node may have up to two children. In practice, binary heaps are enough and we concentrate on binary min heaps and binary max heaps for the remaining discussion.
Representing Heaps:
Before looking at heap operations, let us see how heaps can be represented. One possibility is using arrays. Since heaps are forming complete binary trees, there will not be any wastage of locations. For the discussion below let us assume that elements are stored in arrays, which starts at index 0. The previous max heap can be represented as:

Note: For the remaining discussion let us assume that we are doing manipulations in max heap.
Declaration of Heap
int Parent (struct Heap* h, int i) { if(i <= 0 || i>=h-count) return -1;
return i-1/2;
Creating Heap
struct Heap CreateHeap(int capacity, int heap_type) { struct Heap * h = (struct Heap *)malloc(sizeof(struct Heap)); if(h == NULL) {
}
printf("Memory Error");
return;
h-heap_type = heap_type; h-count=0;
h-capacity = capacity;
h-array (int *)malloc(sizeof(int) *h-capacity);
}
if(h-array = NULL) {
printf("Memory Error");
return;
return h;
Time Complexity: O(1).
Parent of a Node For a node at i th location, its parent is at i-1/2 location. In the previous example, the element 6 is at second location and its parent is at 0 th location.
struct Heap { int *array;
int count;
int capacity;
// Number of elements in Heap // Size of the heap
int heap_type;
// Min Heap or Max Heap
Children of a Node
Similar to the above discussion, for a node at i th location, its children are at 2 * i + 1 and 2 * i + 2 locations. For example, in the above tree the element 6 is at second location and its children 2 and 5 are at 5 (2 * i + 1 = 2 * 2 + 1) and 6(2 * i + 2 = 2 * 2) locations.
int LeftChild(struct Heap *h, int i) { int left = 2* i + 1;
}
if(left >= h-count)
return -1;
return left;
Time Complexity: 0(1),
int RightChild(struct Heap *h, int i) { int right = 2* i + 2; if(right >= h-count) return -1;
}
return right;
Time Complexity: O(1).
Getting the Maximum Element
Since the maximum element in max heap is always at root, it will be stored at h→array[O].
int GetMaximum(Heap *h) { if(h-count == 0) return -1;
return h-array[0];
Time Complexity: O(1).
Heapifying an Element
After inserting an element into heap, it may not satisfy the heap property. In that case we need to adjust the locations of the heap to make it heap again. This process is called heapifying. In maxheap, to heapify an element, we have to find the maximum of its children and swap it with the current element and continue this process until the heap property is satisfied at every node.
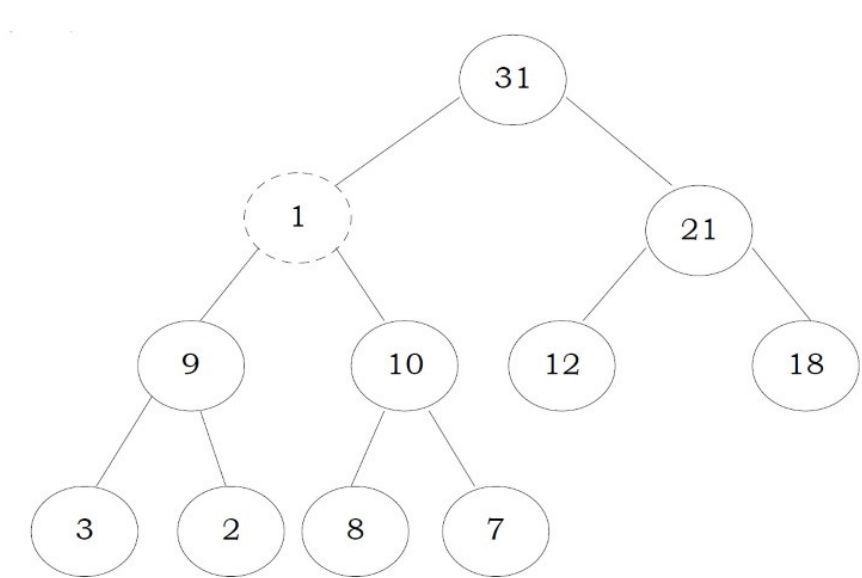
Observation: One important property of heap is that, if an element is not satisfying the heap property, then all the elements from that element to the root will have the same problem. In the example below, element 1 is not satisfying the heap property and its parent 31 is also having the issue. Similarly, if we heapify an element, then all the elements from that element to the root will also satisfy the heap property automatically. Let us go through an example. In the above heap, the element 1 is not satisfying the heap property. Let us try heapifying this element.
To heapify 1, find the maximum of its children and swap with that.

We need to continue this process until the element satisfies the heap properties. Now, swap 1 with 8.

Now the tree is satisfying the heap property. In the above heapifying process, since we are moving from top to bottom, this process is sometimes called percolate down. Similarly, if we start heapifying from any other node to root, we can that process percolate up as move from bottom to top.
int Insert(struct Heap *h, int data) {
int i;
if(h-count=h-capacity) ResizeHeap(h);
h-count++;
i=h-count-1;
//increasing the heap size to hold this new item
}
while(i>=0 && data> h-array[(i-1)/2]) {
h-array[i]=h-array[(i-1)/2];
i=i-1/2;
h-array[i] = data;
void Resize Heap(struct Heap * h) {
}
int *array_old = h-array;
h-array = (int)malloc(sizeof(int) h-capacity * 2);
if(h-array == NULL) {
printf("Memory Error");
return;
for (int i=0; i<h-capacity; i++)
h-array[i] = array_old[i];
h-capacity *= 2;
free(array_old);
Time Complexity: O(logn). Heap is a complete binary tree and in the worst case we start at the root and come down to the leaf. This is equal to the height of the complete binary tree. Space Complexity: O(1).
Deleting an Element
To delete an element from heap, we just need to delete the element from the root. This is the only operation (maximum element) supported by standard heap. After deleting the root element, copy the last element of the heap (tree) and delete that last element.
After replacing the last element, the tree may not satisfy the heap property. To make it heap again, call the PercolateDown function.
• Copy the first element into some variable
• Copy the last element into first element location
• PercolateDown the first element
int DeleteMax(struct Heap *h) { int data; if(h-count == 0) return -1;
data = h-array[0];
h-array[0]=h-array[h-count-1];
h-count--; //reducing the heap size
PercolateDown(h, 0);
return data;
Note: Deleting an element uses PercolateDown, and inserting an element uses PercolateUp. Time Complexity: same as Heapify function and it is O(logn).
Inserting an Element Insertion of an element is similar to the heapify and deletion process.
• Increase the heap size
• Keep the new element at the end of the heap (tree)
• Heapify the element from bottom to top (root)
Before going through code, let us look at an example. We have inserted the element 19 at the end of the heap and this is not satisfying the heap property.

in order to heapify this element (19) , we need to compare with parent and adjust them.
swapping them 19 and 14 gives:
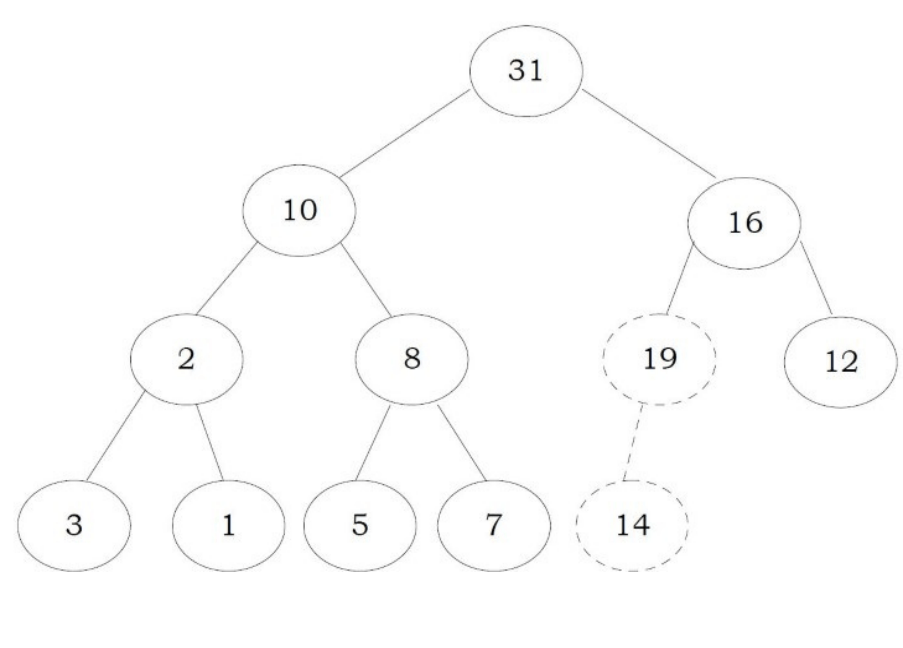
Again, swap 19 and 16:

Now the tree is satisfying the heap property. Since we are following the bottom-up approach we sometimes call this process percolate up.
void DestroyHeap (struct Heap *h) { if(h == NULL) return; free(h-array);
free(h); h = NULL;
Time Complexity: O(logn). The explanation is the same as that of the Heapify function.
Destroying Heap
int Insert(struct Heap *h, int data) {
int i;
if(h-count=h-capacity) ResizeHeap(h);
h-count++;
i=h-count-1;
//increasing the heap size to hold this new item
}
while(i>=0 && data> h-array[(i-1)/2]) {
h-array[i]=h-array[(i-1)/2];
i=i-1/2;
h-array[i] = data;
void Resize Heap(struct Heap * h) {
}
int *array_old = h-array;
h-array = (int)malloc(sizeof(int) h-capacity * 2);
if(h-array == NULL) {
printf("Memory Error");
return;
for (int i=0; i<h-capacity; i++)
h-array[i] = array_old[i];
h-capacity *= 2;
free(array_old);
Heapifying the Array
One simple approach for building the heap is, take n input items and place them into an empty heap. This can be done with n successive inserts and takes O(nlogn) in the worst case. This is due to the fact that each insert operation takes O(logn).
To finish our discussion of binary heaps, we will look at a method to build an entire heap from a list of keys. The first method you might think of may be like the following. Given a list of keys, you could easily build a heap by inserting each key one at a time. Since you are starting with a list of one item, the list is sorted and you could use binary search to find the right position to insert the next key at a cost of approximately O(logn) operations.
next key at a cost of approximately O(logn) operations. However, remember that inserting an item in the middle of the list may require O(n) operations to shift the rest of the list over to make room for the new key. Therefore, to insert n keys into the heap would require a total of O(nlogn) operations. However, if we start with an entire list then we can build the whole heap in O(n) operations.
Observation: Leaf nodes always satisfy the heap property and do not need to care for them. The leaf elements are always at the end and to heapify the given array it should be enough if we heapify the non-leaf nodes. Now let us concentrate on finding the first non-leaf node. The last element of the heap is at location h → count – 1, and to find the first non-leaf node it is enough to find the parent of the last element.
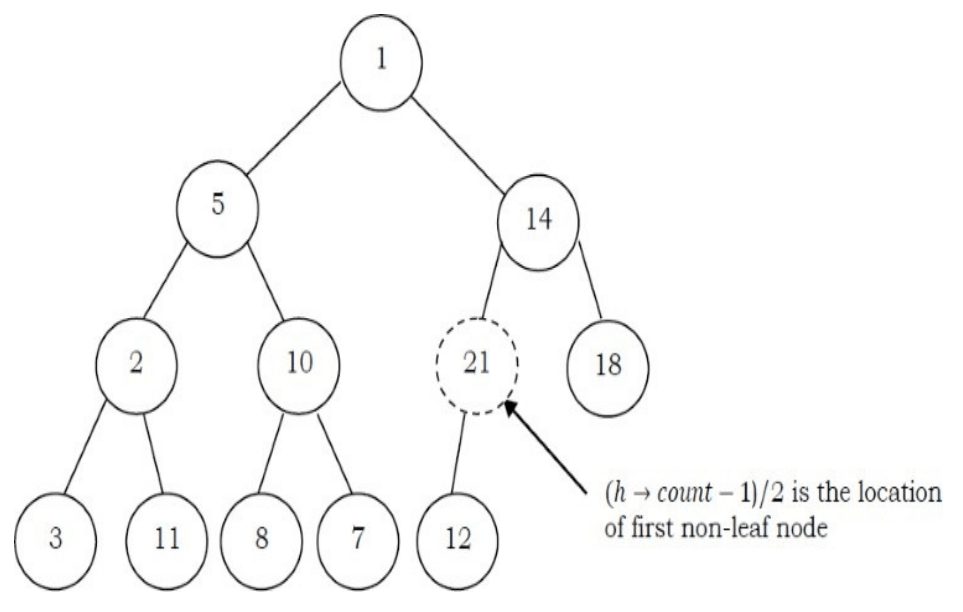
void BuildHeap(struct Heap *h, int A[], int n) { if(h == NULL) return;
while (n>h-capacity) ResizeHeap(h); for (int i = 0; i < n; i++) h-array[i] =A[i];
h-count = n;
for (int i = (n-1)/2; i >=0; i--)
PercolateDown(h, i);
Time Complexity: The linear time bound of building heap can be shown by computing the sum of the heights of all the nodes. For a complete binary tree of height h containing n = 2 h+1 – 1 nodes, the sum of the heights of the nodes is n – h – 1 = n – logn – 1 (for proof refer to Problems Section). That means, building the heap operation can be done in linear time (O(n)) by applying a PercolateDown function to the nodes in reverse level order.
7.7 Heapsort
One main application of heap ADT is sorting (heap sort). The heap sort algorithm inserts all elements (from an unsorted array) into a heap, then removes them from the root of a heap until the heap is empty. Note that heap sort can be done in place with the array to be sorted. Instead of deleting an element, exchange the first element (maximum) with the last element and reduce the heap size (array size). Then, we heapify the first element. Continue this process until the number of remaining elements is one.
void Heapsort(int A[], in n) { struct Heap *h = CreateHeap(n);
int old_size, i, temp; BuildHeap(h, A, n);
old_size = h-count; for(i=n-1; i > 0; i--) {
}
//h-array [0] is the largest element temp = h-array[0];
h-array[0]=h-array[h-count-1]; h-array[0] = temp; h-count--; PercolateDown(h, 0);
h-count = old_size;
Time complexity: As we remove the elements from the heap, the values become sorted (since maximum elements are always root only). Since the time complexity of both the insertion algorithm and deletion algorithm is O(logn) (where n is the number of items in the heap), the time complexity of the heap sort algorithm is O(nlogn).
7.8 Priority Queues [Heaps]: Problems & Solutions
Problem-1 What are the minimum and maximum number of elements in a heap of height h?
Solution: Since heap is a complete binary tree (all levels contain full nodes except possibly the lowest level), it has at most 2 h+1 – 1 elements (if it is complete). This is because, to get maximum nodes, we need to fill all the h levels completely and the maximum number of nodes is nothing but the sum of all nodes at all h levels.
To get minimum nodes, we should fill the h – 1 levels fully and the last level with only one element. As a result, the minimum number of nodes is nothing but the sum of all nodes from h – 1 levels plus 1 (for the last level) and we get 2 h – 1 + 1 = 2 h elements (if the lowest level has just 1 element and all the other levels are complete).
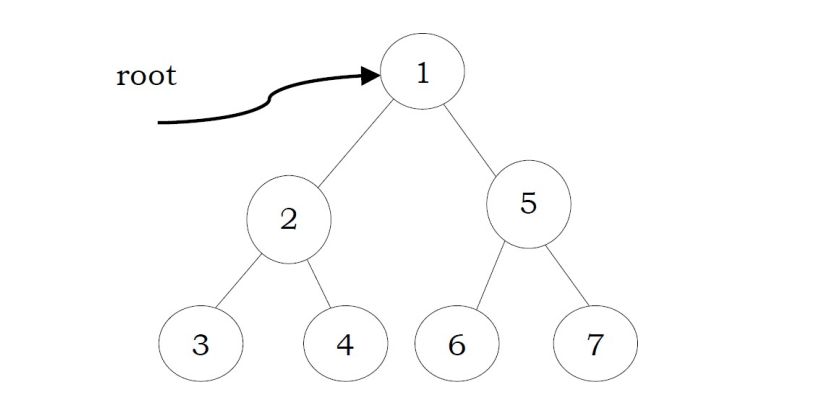
Problem-2 Is there a min-heap with seven distinct elements so that the preorder traversal of
it gives the elements in sorted orde?
Solution: Yes. For the tree below, preorder traversal produces ascending order.
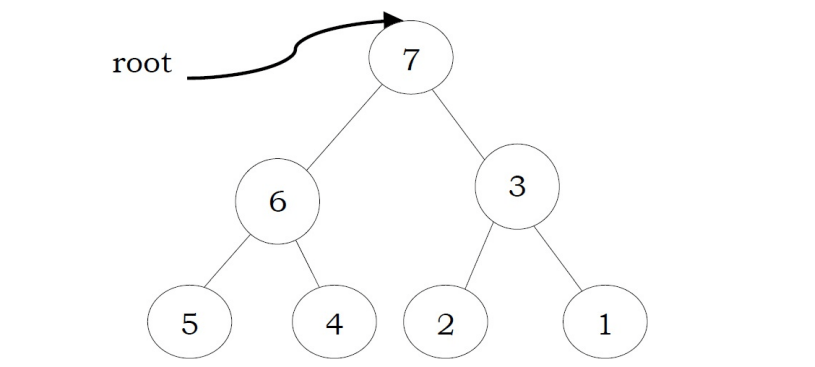
Problem-3 Is there a max-heap with seven distinct elements so that the preorder traversal of it gives the elements in sorted order?
Solution: Yes. For the tree below, preorder traversal produces descending order.
Problem-4 Is there a min-heap/max-heap with seven distinct elements so that the inorder traversal of it gives the elements in sorted order?
Solution: No. Since a heap must be either a min-heap or a max-heap, the root will hold the smallest element or the largest. An inorder traversal will visit the root of the tree as its second step, which is not the appropriate place if the tree’s root contains the smallest or largest element.
Problem-5 Is there a min-heap/max-heap with seven distinct elements so that the postorder traversal of it gives the elements in sorted order?
Solution:
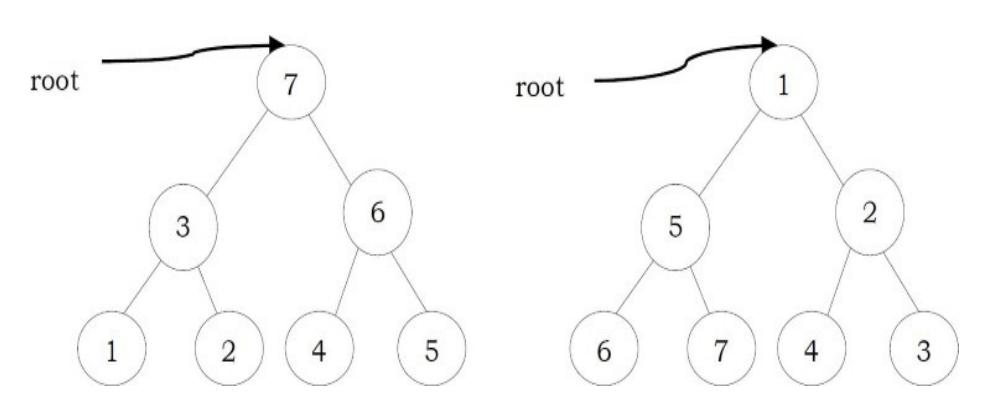
Yes, if the tree is a max-heap and we want descending order (below left), or if the tree is a minheap and we want ascending order (below right).
Problem-6 Show that the height of a heap with n elements is logn?
Solution: A heap is a complete binary tree. All the levels, except the lowest, are completely full. A heap has at least 2 h elements and at most elements 2 h ≤ n ≤ 2 h+1 – 1. This implies, h ≤ logn ≤ h + 1. Since h is an integer, h = logn.
Problem-7 Given a min-heap, give an algorithm for finding the maximum element.
solution: For a given min heap, the maximum element will always be at leaf only. Now, the next question is how to find the leaf nodes in the tree.
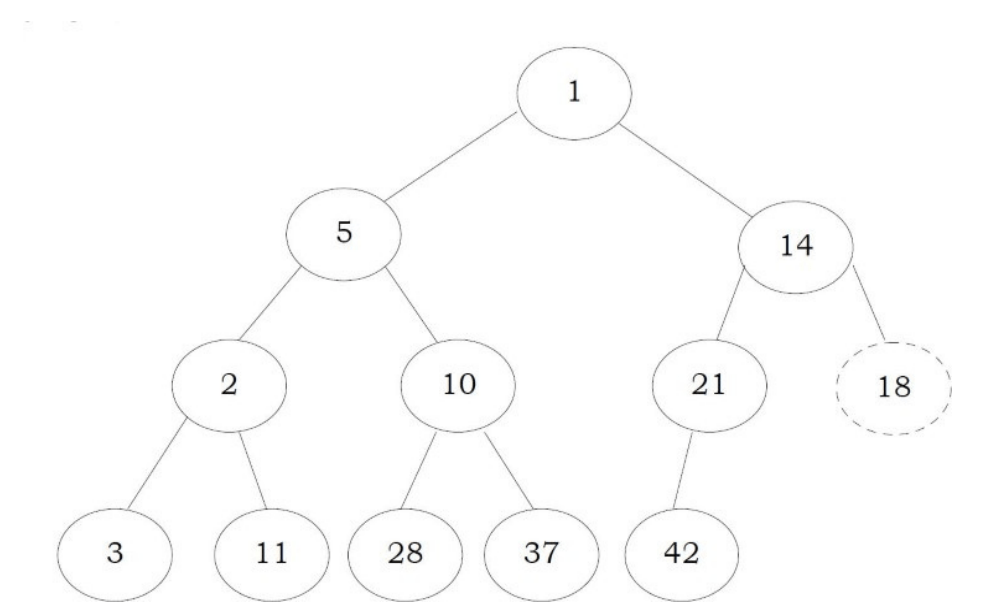
If we carefully observe, the next node of the last element’s parent is the first leaf node. Since the last element is always at the h → count – 1 th location, the next node of its parent (parent at location h -> count -1/2 can be calculated as
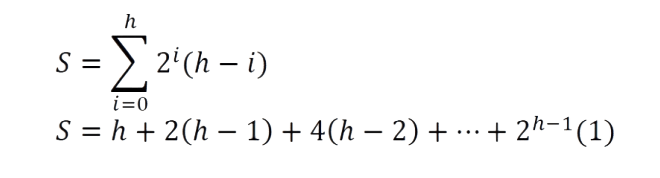
Now, the only step remaining is scanning the leaf nodes and finding the maximum among them.
int FindMaxInMinHeap(struct Heap *h) { int Max = -1;
for(int i= (h-count+1)/2; i < h→count; i++) if(h-array[i] > Max) Max = h-array[i];
Time Complexity: O(n/2)≈ O (n/2)
Problem-8 Give an algorithm for deleting an arbitrary element from min heap.
Solution: To delete an element, first we need to search for an element. Let us assume that we are using level order traversal for finding the element. After finding the element we need to follow the DeleteMin process.
Time Complexity = Time for finding the element + Time for deleting an element
= O(n) + O (logn) ≈ O(n). //Time for searching is dominated.
Problem-9 Give an algorithm for deleting the i th indexed element in a given min-heap.
Solution:
int Delete(struct Heap *h, int i) {
int key; if(n <i){
}
printf("Wrong position");
return;
key = h-array[i];
h-array[i]= h-array[h-count-1];
h-count--;
Percolate Down(h, i); return key;
Time Complexity = O(logn).
Problem-10 Prove that, for a complete binary tree of height h the sum of the height of all nodes is O(n – h).
Solution: A complete binary tree has 2 i nodes on level (.Also, a node on level i has depth i and height h – i. Let us assume that S denotes the sum of the heights of all these nodes and S can be calculated as:
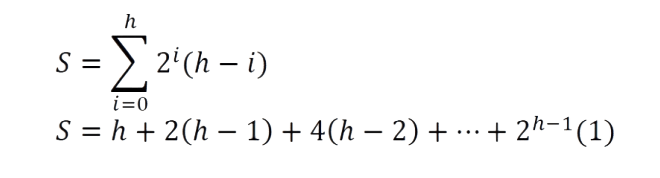
Multiplying with 2 on both sides gives: 2S = 2h + 4(h – 1) + 8(h – 2) + ···+ 2 h – 1 (1)
Now, subtract S from 2S: 2S – S = – h + 2 + 4 + ··· + 2 h ⇒ S = (2 h+1 – 1) – (h – 1)
But, we already know that the total number of nodes n in a complete binary tree with height h is n = 2 h+1 – 1. This gives us: h = log(n + 1).
Finally, replacing 2 h+1 – 1 with n, gives: S = n – (h – 1) = O(n – logn) = O(n – h).
Problem-11 Give an algorithm to find all elements less than some value of k in a binary heap.
Solution: Start from the root of the heap. If the value of the root is smaller than k then print its value and call recursively once for its left child and once for its right child. If the value of a node is greater or equal than k then the function stops without printing that value.
The complexity of this algorithm is O(n), where n is the total number of nodes in the heap. This bound takes place in the worst case, where the value of every node in the heap will be smaller than k, so the function has to call each node of the heap.
Problem-12 Give an algorithm for merging two binary max-heaps. Let us assume that the size of the first heap is m + n and the size of the second heap is n.
Solution: One simple way of solving this problem is:
• Assume that the elements of the first array (with size m + n) are at the beginning. That means, first m cells are filled and remaining n cells are empty.
• Without changing the first heap, just append the second heap and heapify the array.
• Since the total number of elements in the new array is m + n, each heapify operation takes O(log(m + n)).
The complexity of this algorithm is : O((m + n)log(m + n)).
Problem-13 Can we improve the complexity of Problem-12?
Solution: Instead of heapifying all the elements of the m + n array, we can use the technique of “building heap with an array of elements (heapifying array)”. We can start with non-leaf nodes and heapify them. The algorithm can be given as:
• Assume that the elements of the first array (with size m + n) are at the beginning. That means, the first m cells are filled and the remaining n cells are empty.
• Without changing the first heap, just append the second heap.
• Now, find the first non-leaf node and start heapifying from that element.
In the theory section, we have already seen that building a heap with n elements takes O(n) complexity. The complexity of merging with this technique is: O(m + n).
Problem-14 Is there an efficient algorithm for merging 2 max-heaps (stored as an array)? Assume both arrays have n elements.
Solution: The alternative solution for this problem depends on what type of heap it is. If it’s a standard heap where every node has up to two children and which gets filled up so that the leaves are on a maximum of two different rows, we cannot get better than O(n) for the merge.
There is an O(logm × logn) algorithm for merging two binary heaps with sizes m and n. For m = n, this algorithm takes O(log 2n) time complexity. We will be skipping it due to its difficulty and scope.
For better merging performance, we can use another variant of binary heap like a FibonacciHeap which can merge in O(1) on average (amortized).
Problem-15 Give an algorithm for finding the k th smallest element in min-heap.
Solution: One simple solution to this problem is: perform deletion k times from min-heap
return PQ.Min();
//Just delete first k-1 elements and return the k-th element.
for(int i=0;i<k-1;i++) DeleteMin(h);
return DeleteMin(h);
Time Complexity: O(klogn). Since we are performing deletion operation k times and each deletion takes O(logn).
Problem-16 For Problem-15, can we improve the time complexity?
Solution: Assume that the original min-heap is called HOrig and the auxiliary min-heap is named HAux. Initially, the element at the top of HOrig, the minimum one, is inserted into HAux. Here we don’t do the operation of DeleteMin with HOrig.
void Push(int element) { PQ.Insert(c, element);
}
C--;
int Pop() {
}
return PQ.DeleteMin();
int Top(){
return PQ.Min();
}
int Size() {
}
return PQ.Size();
int IsEmpty() { return PQ.IsEmpty();
Every while-loop iteration gives the k th smallest element and we need k loops to get the k th smallest elements. Because the size of the auxiliary heap is always less than k, every while-loop iteration the size of the auxiliary heap increases by one, and the original heap HOrig has no operation during the finding, the running time is O(klogk).
Note: The above algorithm is useful if the k value is too small compared to n. If the k value is approximately equal to n, then we can simply sort the array (let’s say, using couting sort or any other linear sorting algorithm) and return k th smallest element from the sorted array. This gives O(n) solution.
Problem-17 Find k max elements from max heap.
Solution: One simple solution to this problem is: build max-heap and perform deletion k times. T(n) = DeleteMin from heap k times = Θ(klogn).
Problem-18 For Problem-17, is there any alternative solution?
Solution: We can use the Problem-16 solution. At the end, the auxiliary heap contains the klargest elements. Without deleting the elements we should keep on adding elements to HAux.
Problem-19 How do we implement stack using heap?
Solution: To implement a stack using a priority queue PQ (using min heap), let us assume that we are using one extra integer variable c. Also, assume that c is initialized equal to any known value (e.g., 0). The implementation of the stack ADT is given below. Here c is used as the priority while inserting/deleting the elements from PQ.
Heap HOrig; Heap HAux;
int FindKthLargest Ele( int k) {
int heapElement;//Assuming heap data is of integers int count=1;
HAux.Insert(HOrig.Min(); while(true){
//return the minimum element and delete it from the HA heap heapElement = HAux.DeleteMin();
if(++count == k) {
return heapElement;
}
else { //insert the left and right children in HO into the HA
HAux.Insert(heapElement.LeftChild()); HAux.Insert(heapElement. RightChild());
We could also increment c back when popping.
Observation: We could use the negative of the current system time instead of c (to avoid overflow). The implementation based on this can be give
void Push(int element) { PQ.insert(-gettime(), element);
Problem-20 How do we implement Queue using heap?
Solution: To implement a queue using a priority queue PQ (using min heap), as similar to stacks simulation, let us assume that we are using one extra integer variable, c. Also, assume that c is initialized equal to any known value (e.g., 0). The implementation of the queue ADT is given below. Here the c is used as the priority while inserting/deleting the elements from PQ.
void Push(int element) { PQ.insert(gettime(), element);
Note: We could also decrement c when popping.
Observation: We could use just the negative of the current system time instead of c (to avoid overflow). The implementation based on this can be given as:
void Push(int element) { PQ.Insert(c, element);
}
}
C++;
int Pop() {
return PQ.DeleteMin();
int Top() {
return PQ.Min();
}
int Size() {
}
return PQ.Size();
int IsEmpty(){
return PQ.IsEmpty();
Note: The only change is that we need to take a positive c value instead of negative.
Problem-21 Given a big file containing billions of numbers, how can you find the 10 maximum numbers from that file?
Solution: Always remember that when you need to find max n elements, the best data structure to use is priority queues.
One solution for this problem is to divide the data in sets of 1000 elements (let’s say 1000) and make a heap of them, and then take 10 elements from each heap one by one. Finally heap sort all the sets of 10 elements and take the top 10 among those. But the problem in this approach is where to store 10 elements from each heap. That may require a large amount of memory as we have billions of numbers
Reusing the top 10 elements (from the earlier heap) in subsequent elements can solve this problem. That means take the first block of 1000 elements and subsequent blocks of 990 elements each. Initially, Heapsort the first set of 1000 numbers, take max 10 elements, and mix them with 990 elements of the 2 nd set. Again, Heapsort these 1000 numbers (10 from the first set and 990 from the 2 nd set), take 10 max elements, and mix them with 990 elements of the 3 rd set. Repeat till the last set of 990 (or less) elements and take max 10 elements from the final heap. These 10 elements will be your answer.
Time Complexity: O(n) = n/1000 ×(complexity of Heapsort 1000 elements) Since complexity of heap sorting 1000 elements will be a constant so the O(n) = n i.e. linear complexity
Problem-22 Merge k sorted lists with total of n elements: We are given k sorted lists with total n inputs in all the lists. Give an algorithm to merge them into one single sorted list.
Solution: Since there are k equal size lists with a total of n elements, the size of each list is One simple way of solving this problem is:
• Take the first list and merge it with the second list. Since the size of each list is , this step produces a sorted list with size . This is similar to merge sort logic. The time complexity of this step is: . This is because we need to scan all the elements of both the lists.
• Then, merge the second list output with the third list. As a result, this step produces a sorted list with size . The time complexity of this step is: . This is because we need to scan all the elements of both lists (one with size and the other with size ).
• Continue this process until all the lists are merged to one list.

Problem-23 For Problem-22, can we improve the time complexity?
Solution:
1 Divide the lists into pairs and merge them. That means, first take two lists at a time and merge them so that the total elements parsed for all lists is O(n). This operation gives k/2 lists.
2 Repeat step-1 until the number of lists becomes one.
Time complexity: Step-1 executes logk times and each operation parses all n elements in all the lists for making k/2 lists. For example, if we have 8 lists, then the first pass would make 4 lists by parsing all n elements. The second pass would make 2 lists by again parsing n elements and the third pass would give 1 list by again parsing n elements. As a result the total time complexity is O(nlogn).
Space Complexity: O(n).
Problem-24 For Problem-23, can we improve the space complexity?
Solution: Let us use heaps for reducing the space complexity.
1. Build the max-heap with all the first elements from each list in O(k).
2. In each step, extract the maximum element of the heap and add it at the end of the output.
3. Add the next element from the list of the one extracted. That means we need to select the next element of the list which contains the extracted element of the previous step.
4. Repeat step-2 and step-3 until all the elements are completed from all the lists.
Time Complexity = O(nlogk ). At a time we have k elements max-heap and for all n elements we have to read just the heap in logk time, so total time = O(nlogk). Space Complexity: O(k) [for Max-heap].
Problem-25 Given 2 arrays A and B each with n elements. Give an algorithm for finding largest n pairs (A[i],B[j]).
Solution:
Algorithm:
• Heapify A and B. This step takes O(2n) ≈ O(n).
• Then keep on deleting the elements from both the heaps. Each step takes O(2logn) ≈ O(logn).
Total Time complexity: O(nlogn).
Problem-26 Min-Max heap: Give an algorithm that supports min and max in O(1) time, insert, delete min, and delete max in O(logn) time. That means, design a data structure which supports the following operations:
Solution: This problem can be solved using two heaps. Let us say two heaps are: Minimum-Heap Hmin and Maximum-Heap Hmax . Also, assume that elements in both the arrays have mutual pointers. That means, an element in Hmin will have a pointer to the same element in Hmax and an element in Hmax will have a pointer to the same element in Hmin .

Problem-27 Dynamic median finding. Design a heap data structure that supports finding the median.
Solution: In a set of n elements, median is the middle element, such that the number of elements lesser than the median is equal to the number of elements larger than the median. If n is odd, we can find the median by sorting the set and taking the middle element. If n is even, the median is usually defined as the average of the two middle elements. This algorithm works even when some of the elements in the list are equal. For example, the median of the multiset {1, 1, 2, 3, 5} is 2, and the median of the multiset {1, 1, 2, 3, 5, 8} is 2.5.
“Median heaps” are the variant of heaps that give access to the median element. A median heap can be implemented using two heaps, each containing half the elements. One is a max-heap, containing the smallest elements; the other is a min-heap, containing the largest elements. The size of the max-heap may be equal to the size of the min-heap, if the total number of elements is even. In this case, the median is the average of the maximum element of the max-heap and the minimum element of the min-heap. If there is an odd number of elements, the max-heap will contain one more element than the min-heap. The median in this case is simply the maximum element of the max-heap.
Problem-28 Maximum sum in sliding window: Given array A[] with sliding window of size w which is moving from the very left of the array to the very right. Assume that we can only see the w numbers in the window. Each time the sliding window moves rightwards by one position. For example: The array is [1 3 -1 -3 5 3 6 7], and w is 3.

Input: A long array A[], and a window width w. Output: An array B[], B[i] is the maximum value of from A[i] to A[i+w-1]
Requirement: Find a good optimal way to get B[i] Solution: Brute force solution is, every time the window is moved we can search for a total of w elements in the window. Time complexity: O(nw).
Problem-29 For Problem-28, can we reduce the complexity?
Solution: Yes, we can use heap data structure. This reduces the time complexity to O(nlogw). Insert operation takes O(logw) time, where w is the size of the heap. However, getting the maximum value is cheap; it merely takes constant time as the maximum value is always kept in the root (head) of the heap. As the window slides to the right, some elements in the heap might not be valid anymore (range is outside of the current window). How should we remove them? We would need to be somewhat careful here. Since we only remove elements that are out of the window’s range, we would need to keep track of the elements’ indices too.
Problem-30 For Problem-28, can we further reduce the complexity?
Solution: Yes, The double-ended queue is the perfect data structure for this problem. It supports insertion/deletion from the front and back. The trick is to find a way such that the largest element in the window would always appear in the front of the queue. How would you maintain this requirement as you push and pop elements in and out of the queue?
Besides, you will notice that there are some redundant elements in the queue that we shouldn’t even consider. For example, if the current queue has the elements: [10 5 3], and a new element in the window has the element 11. Now, we could have emptied the queue without considering elements 10, 5, and 3, and insert only element 11 into the queue.
Typically, most people try to maintain the queue size the same as the window’s size. Try to break away from this thought and think out of the box. Removing redundant elements and storing only elements that need to be considered in the queue is the key to achieving the efficient O(n) solution below. This is because each element in the list is being inserted and removed at most once. Therefore, the total number of insert + delete operations is 2n.
void MaxSlidingWindow(int A[], int n, int w, int B[]) { struct Double EndQueue Q = Create Double EndQueue(); for (int i = 0; i < w; i++){
}
while (!IsEmptyQueue(Q) && A[i] >= A[QBack(Q)]) PopBack(Q);
PushBack(Q, i);
for (int i = w; i < n; i++) {
Bi-w] - A[QFront(Q)];
while (!IsEmptyQueue(Q) && A[i] >= A[QBack(Q)])
PopBack(Q);
while (!IsEmptyQueue(Q) && QFront(Q) <= i-w) PopFront(Q);
PushBack(Q, i);
B[n-w] = A(QFront(Q)];
Problem-31
A priority queue is a list of items in which each item has associated with it a priority. Items are withdrawn from a priority queue in order of their priorities starting with the highest priority item first. If the maximum priority item is required, then a heap is constructed such than priority of every node is greater than the priority of its children.
Design such a heap where the item with the middle priority is withdrawn first. If there are n items in the heap, then the number of items with the priority smaller than the middle priority is if n is odd, else ∓ 1.
Explain how withdraw and insert operations work, calculate their complexity, and how the data structure is constructed.
Solution: We can use one min heap and one max heap such that root of the min heap is larger than the root of the max heap. The size of the min heap should be equal or one less than the size of the max heap. So the middle element is always the root of the max heap.
For the insert operation, if the new item is less than the root of max heap, then insert it into the max heap; else insert it into the min heap. After the withdraw or insert operation, if the size of heaps are not as specified above than transfer the root element of the max heap to min heap or vice-versa.
With this implementation, insert and withdraw operation will be in O(logn) tim
Problem-32 Given two heaps, how do you merge (union) them?
Solution: Binary heap supports various operations quickly: Find-min, insert, decrease-key. If we have two min-heaps, H1 and H2, there is no efficient way to combine them into a single min-heap.
For solving this problem efficiently, we can use mergeable heaps. Mergeable heaps support efficient union operation. It is a data structure that supports the following operations:
• Create-Heap(): creates an empty heap
• Insert(H,X,K) : insert an item x with key K into a heap H
• Find-Min(H) : return item with min key
• Delete-Min(H) : return and remove
• Union(H1, H2) : merge heaps H1 and H2
Examples of mergeable heaps are:
• Binomial Heaps
• Fibonacci Heaps
Both heaps also support:
• Decrease-Key(H,X,K): assign item Y with a smaller key K
• Delete(H,X) : remove item X
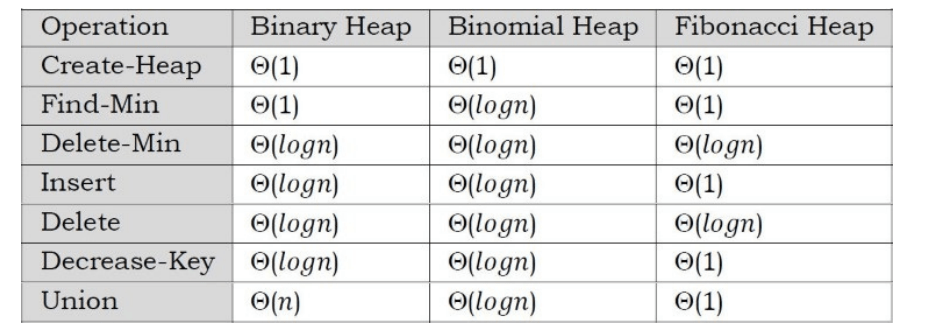
Binomial Heaps: Unlike binary heap which consists of a single tree, a binomial heap consists of a small set of component trees and no need to rebuild everything when union is performed. Each component tree is in a special format, called a binomial tree.
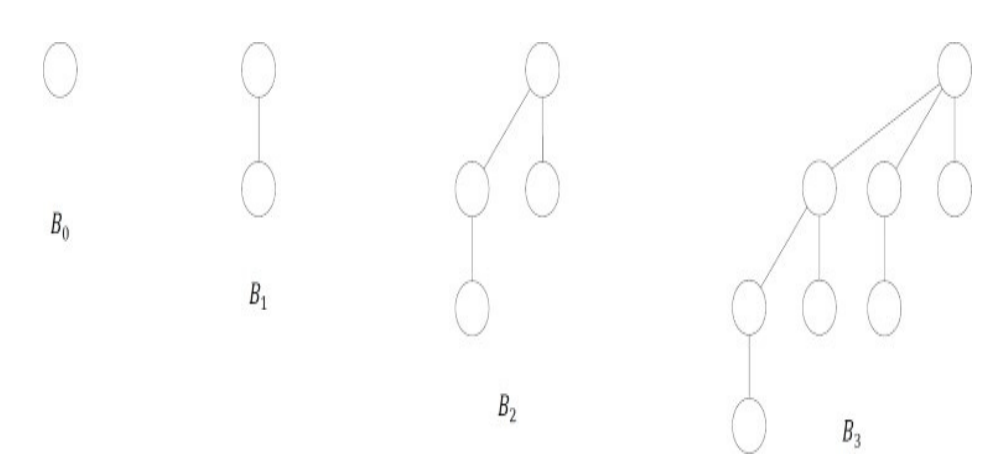
A binomial tree of order k, denoted by Bk is defined recursively as follows
• B0 is a tree with a single node
• For k ≥ 1, Bk is formed by joining two Bk–1 , such that the root of one tree becomes the leftmost child of the root of the other.
Example:
Fibonacci Heaps: Fibonacci heap is another example of mergeable heap. It has no good worstcase guarantee for any operation (except Insert/Create-Heap). Fibonacci Heaps have excellent amortized cost to perform each operation. Like binomial heap, fibonacci heap consists of a set of min-heap ordered component trees. However, unlike binomial heap, it has
• No limit on number of trees (up to O(n)), and
• No limit on height of a tree (up to O(n))
Also, Find-Min, Delete-Min, Union, Decrease-Key, Delete all have worst-case O(n) running time. However, in the amortized sense, each operation performs very quickly.
Problem-33 Median in an infinite series of integers
Solution: Median is the middle number in a sorted list of numbers (if we have odd number of elements). If we have even number of elements, median is the average of two middle numbers in a sorted list of numbers
We can solve this problem efficiently by using 2 heaps: One MaxHeap and one MinHeap.
1. MaxHeap contains the smallest half of the received integers
2. MinHeap contains the largest half of the received integers
The integers in MaxHeap are always less than or equal to the integers in MinHeap. Also, the number of elements in MaxHeap is either equal to or 1 more than the number of elements in the MinHeap.
In the stream if we get 2n elements (at any point of time), MaxHeap and MinHeap will both contain equal number of elements (in this case, n elements in each heap). Otherwise, if we have received 2n + 1 elements, MaxHeap will contain n + 1 and MinHeap n.
Let us find the Median: If we have 2n + 1 elements (odd), the Median of received elements will be the largest element in the MaxHeap (nothing but the root of MaxHeap). Otherwise, the Median of received elements will be the average of largest element in the MaxHeap (nothing but the root of MaxHeap) and smallest element in the MinHeap (nothing but the root of MinHeap). This can be calculated in O(1).
Inserting an element into heap can be done in O(logn). Note that, any heap containing n + 1 elements might need one delete operation (and insertion to other heap) as well.
Example:
Insert 1: Insert to MaxHeap.
MaxHeap: {1}, MinHeap:{}
Insert 9: Insert to MinHeap. Since 9 is greater than 1 and MinHeap maintains the maximum elements.
MaxHeap: {1}, MinHeap:{9}
Insert 2: Insert MinHeap. Since 2 is less than all elements of MinHeap.
MaxHeap: {1,2}, MinHeap:{9}
Insert 0: Since MaxHeap already has more than half; we have to drop the max element from MaxHeap and insert it to MinHeap. So, we have to remove 2 and insert into MinHeap. With that it becomes: MaxHeap: {1}, MinHeap:{2,9} Now, insert 0 to MaxHeap. Total Time Complexity: O(logn).
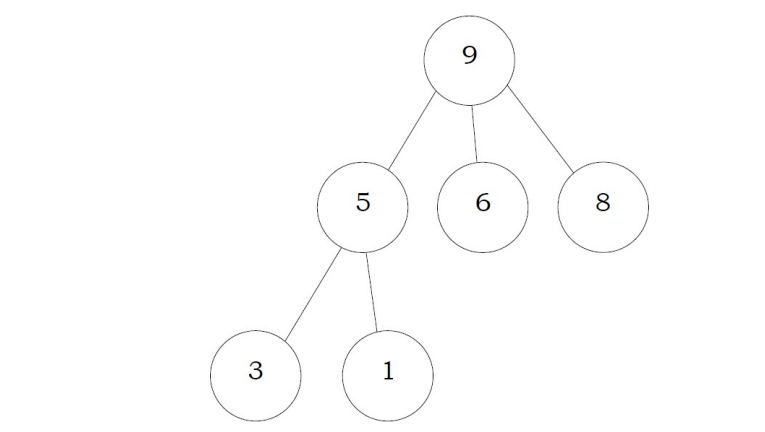
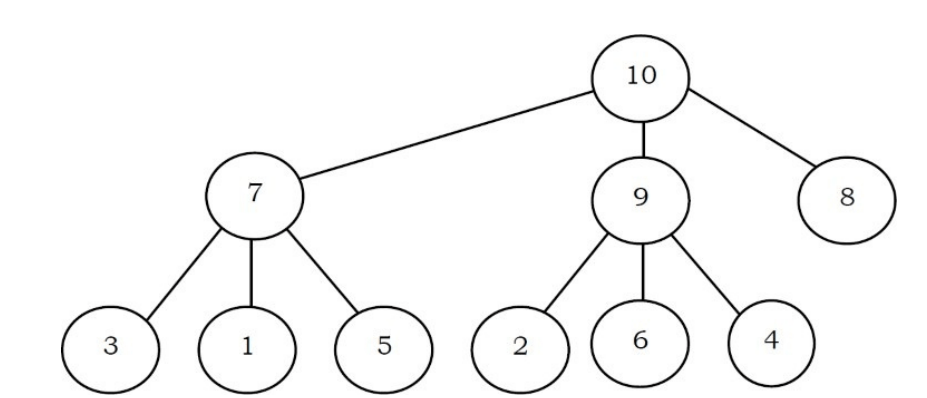
Suppose the elements 7, 2, 10 and 4 are inserted, in that order, into the valid 3- ary max heap found in the above question, Which one of the following is the sequence of items in the array representing the resultant heap?
(A) 10, 7, 9, 8, 3, 1, 5, 2, 6, 4
(B) 10, 9, 8, 7, 6, 5, 4, 3, 2, 1
(C) 10, 9, 4, 5, 7, 6, 8, 2, 1, 3
(D) 10, 8, 6, 9, 7, 2, 3, 4, 1, 5
Solution: The 3-ary max heap with elements 9, 5, 6, 8, 3, 1 is:
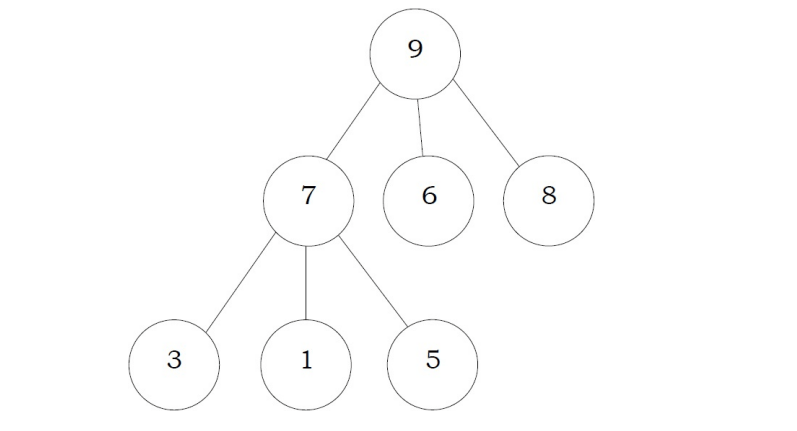
After Insertion of 7:
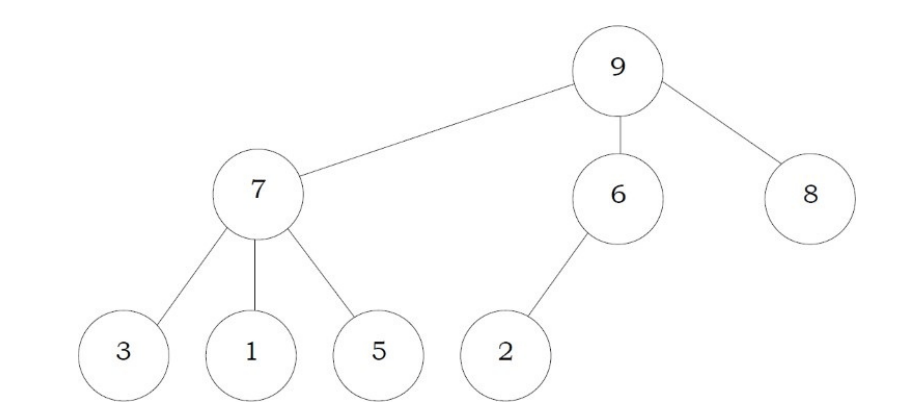
After Insertion of 2:
After Insertion of 10:

After Insertion of 4:
Problem-35 A complete binary min-heap is made by including each integer in [1,1023] exactly once. The depth of a node in the heap is the length of the path from the root of the heap to that node. Thus, the root is at depth 0. The maximum depth at which integer 9 can appear is.
Solution: As shown in the figure below, for a given number i, we can fix the element i at i th level and arrange the numbers 1 to i – 1 to the levels above. Since the root is at depth zero, the maximum depth of the i th element in a min-heap is i – 1. Hence, the maximum depth at which integer 9 can appear is 8

Problem-36 A d-ary heap is like a binary heap, but instead of 2 children, nodes have d children. How would you represent a d-ary heap with n elements in an array? What are the expressions for determining the parent of a given element, Parent(i), and a j th child of a given element, Child(i,j), where 1 ≤ j ≤ d?
Solution: The following expressions determine the parent and j th child of element i (where 1 ≤ j ≤ d):