11.1 What is Searching?
In computer science, searching is the process of finding an item with specified properties from a collection of items. The items may be stored as records in a database, simple data elements in arrays, text in files, nodes in trees, vertices and edges in graphs, or they may be elements of other search spaces.
11.2 Why do we need Searching?
Searching is one of the core computer science algorithms. We know that today’s computers store a lot of information. To retrieve this information proficiently we need very efficient searching algorithms. There are certain ways of organizing the data that improves the searching process. That means, if we keep the data in proper order, it is easy to search the required element. Sorting is one of the techniques for making the elements ordered. In this chapter we will see different searching algorithms.
11.3 Types of Searching
Following are the types of searches which we will be discussing in this book.
• Unordered Linear Search
• Sorted/Ordered Linear Search
• Binary Search
• Interpolation search
• Binary Search Trees (operates on trees and refer Trees chapter)
• Symbol Tables and Hashing
• String Searching Algorithms: Tries, Ternary Search and Suffix Trees
11.4 Unordered Linear Search
Let us assume we are given an array where the order of the elements is not known. That means the elements of the array are not sorted. In this case, to search for an element we have to scan the complete array and see if the element is there in the given list or not.
int UnOrdered LinearSearch (int A[], int n, int data) {
for (int i=0; i < n; i++) {
if(A(i)
==
data)
return i;
return -1;
Time complexity: O(n), in the worst case we need to scan the complete array. Space complexity: O(1).
11.5 Sorted/Ordered Linear Search
If the elements of the array are already sorted, then in many cases we don’t have to scan the complete array to see if the element is there in the given array or not. In the algorithm below, it can be seen that, at any point if the value at A[i] is greater than the data to be searched, then we just return –1 without searching the remaining array.
int Ordered LinearSearch(int A[], int n, int data) { for (int i = 0; i < n; i++) { if(A[i]== data) return i;
else if(A[i]> data) return -1;
return -1;
Time complexity of this algorithm is O(n).This is because in the worst case we need to scan the complete array. But in the average case it reduces the complexity even though the growth rate is the same.
Space complexity: O(1).
Note: For the above algorithm we can make further improvement by incrementing the index at a faster rate (say, 2). This will reduce the number of comparisons for searching in the sorted list.
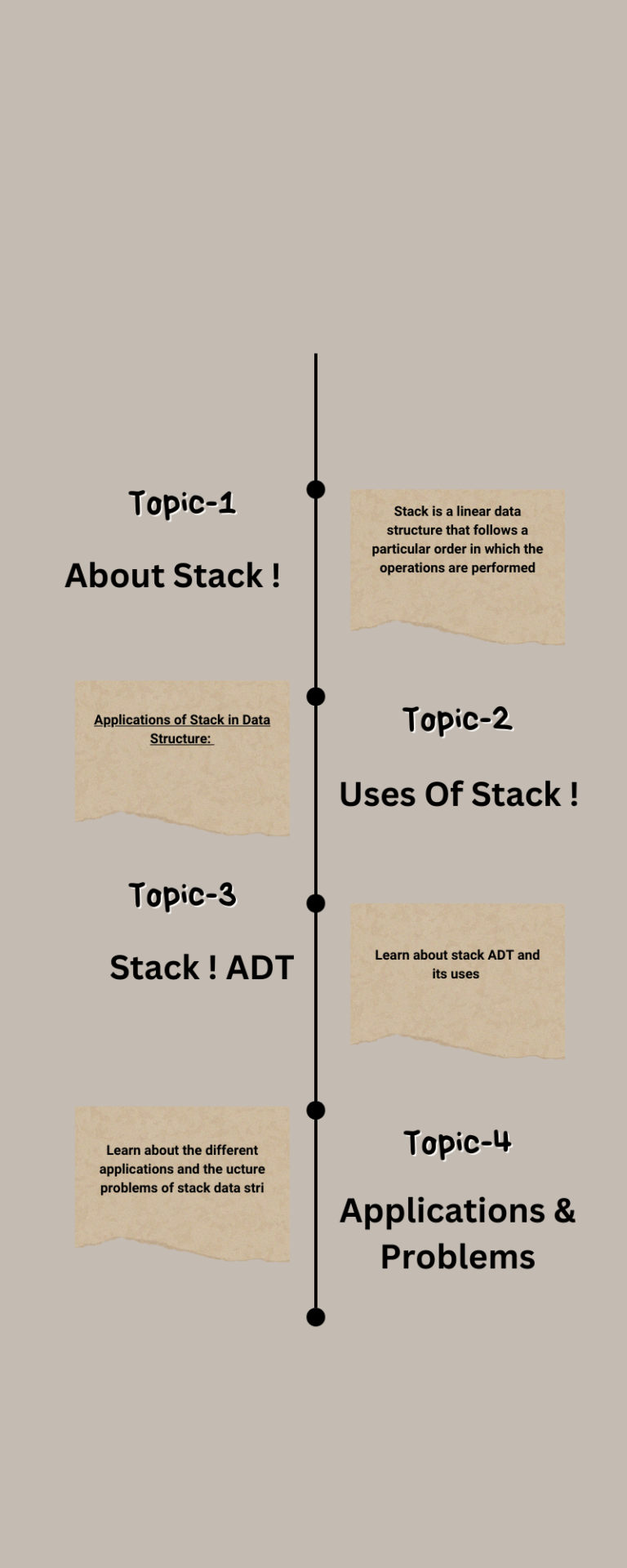
11.6 Binary Search
Let us consider the problem of searching a word in a dictionary. Typically, we directly go to some approximate page [say, middle page] and start searching from that point. If the name that we are searching is the same then the search is complete. If the page is before the selected pages then apply the same process for the first half; otherwise apply the same process to the second half. Binary search also works in the same way. The algorithm applying such a strategy is referred to as binary search algorithm.
}
//Iterative Binary Search Algorithm
int BinarySearchIterative(int A[], int n, int data) { int low = 0;
int high-n-1;
while (low <= high) {
}
mid=low + (high-low)/2; //To avoid overflow
if(A[mid] == data) return mid;
else if(A[mid] < data) low-mid + 1;
else high mid-1;
return -1;
//Recursive Binary Search Algorithm
int BinarySearch Recursive(int A[], int low, int high, int data) { int mid low + (high-low)/2; //To avoid overflow
=
if (low>high) return -1; if(A[mid] == data) return mid;
else if(A[mid] < data)
return BinarySearchRecursive (A, mid + 1, high, data); else return BinarySearchRecursive (A, low, mid-1, data); return -1;
}
Recurrence for binary search is . This is because we are always considering only half of the input list and throwing out the other half. Using Divide and Conquer master theorem, we get, T(n) = O(logn).
Time Complexity: O(logn). Space Complexity: O(1) [for iterative algorithm].
11.7 Interpolation Search
Undoubtedly binary search is a great algorithm for searching with average running time complexity of logn. It always chooses the middle of the remaining search space, discarding one half or the other, again depending on the comparison between the key value found at the estimated (middle) position and the key value sought. The remaining search space is reduced to the part before or after the estimated position.
In the mathematics, interpolation is a process of constructing new data points within the range of a discrete set of known data points. In computer science, one often has a number of data points which represent the values of a function for a limited number of values of the independent variable. It is often required to interpolate (i.e. estimate) the value of that function for an intermediate value of the independent variable.
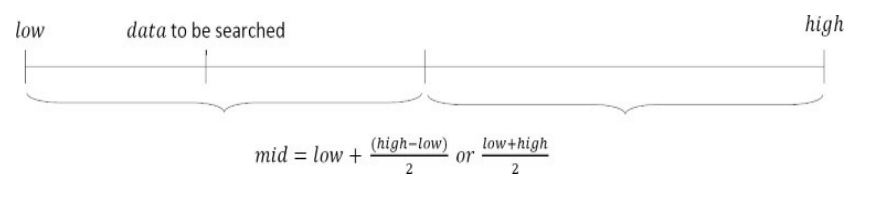
For example, suppose we have a table like this, which gives some values of an unknown function f. Interpolation provides a means of estimating the function at intermediate points, such as x = 55.
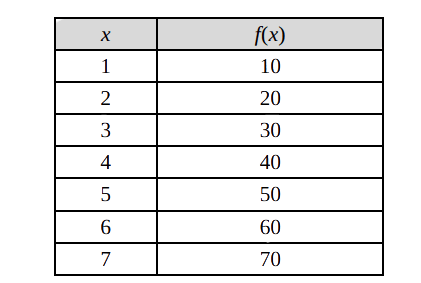
There are many different interpolation methods, and one of the simplest methods is linear interpolation. Since 55 is midway between 50 and 60, it is reasonable to take f(55) midway between f(5) = 50 and f(6) = 60, which yields 55.
Linear interpolation takes two data points, say (x1; y2 ) and (x2 , y2 ), and the interpolant is given by:
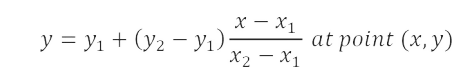
With above inputs, what will happen if we don’t use the constant ½, but another more accurate constant “K”, that can lead us closer to the searched item.

This algorithm tries to follow the way we search a name in a phone book, or a word in the dictionary. We, humans, know in advance that in case the name we’re searching starts with a “m”, like “monk” for instance, we should start searching near the middle of the phone book. Thus if we’re searching the word “career” in the dictionary, you know that it should be placed somewhere at the beginning. This is because we know the order of the letters, we know the interval (a-z), and somehow we intuitively know that the words are dispersed equally. These facts are enough to realize that the binary search can be a bad choice. Indeed the binary search algorithm divides the list in two equal sub-lists, which is useless if we know in advance that the searched item is somewhere in the beginning or the end of the list. Yes, we can use also jump search if the item is at the beginning, but not if it is at the end, in that case this algorithm is not so effective.
The interpolation search algorithm tries to improve the binary search. The question is how to find this value? Well, we know bounds of the interval and looking closer to the image above we can define the following formula
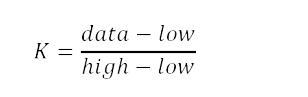
This constant K is used to narrow down the search space. For binary search, this constant K is (low + high)/2.
Now we can be sure that we’re closer to the searched value. On average the interpolation search makes about log (logn) comparisons (if the elements are uniformly distributed), where n is the number of elements to be searched. In the worst case (for instance where the numerical values of the keys increase exponentially) it can make up to O(n) comparisons. In interpolation-sequential search, interpolation is used to find an item near the one being searched for, then linear search is used to find the exact item. For this algorithm to give best results, the dataset should be ordered and uniformly distributed.
void CheckDuplicates Brute Force(int A[], int n) { for(int i = 0; i < n; i++) { for(int j=i+1; j < n; j++) { if(A[i]== Abj])
}
printf("Duplicates exist: %d", A[i]);
return;
}
}
printf("No duplicates in given array.");
11.8 Comparing Basic Searching Algorithms
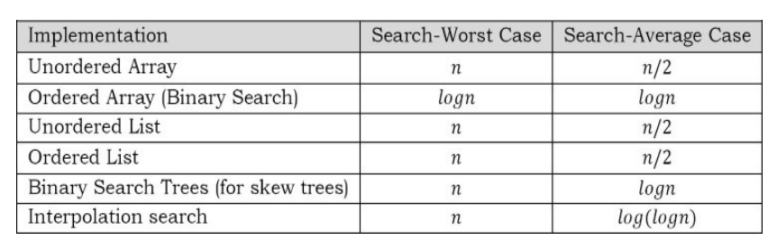
Note: For discussion on binary search trees refer Trees chapter.
11.9 Symbol Tables and Hashing
Refer to Symbol Tables and Hashing chapters.
11.10 String Searching Algorithms
Refer to String Algorithms chapter.
11.11 Searching: Problems & Solutions
Problem-1 Given an array of n numbers, give an algorithm for checking whether there are any duplicate elements in the array or no?
Solution: This is one of the simplest problems. One obvious answer to this is exhaustively searching for duplicates in the array. That means, for each input element check whether there is any element with the same value. This we can solve just by using two simple for loops. The code for this solution can be given as:
int InterpolationSearch(int A[], int data){ int low = 0, mid, high = sizeof(A) - 1; while (low <= high) {
mid=low + (((data - A[low]) (high-low))/(A[high] - A[low])); if (data == A[mid])
return mid + 1;
if (data < A[mid])
else
=
high mid-1;
low = mid + 1;
}
return -1;
Time Complexity: O(n 2 ), for two nested for loops. Space Complexity: O(1).
Problem-2 Can we improve the complexity of Problem-1’s solution?
Solution: Yes. Sort the given array. After sorting, all the elements with equal values will be adjacent. Now, do another scan on this sorted array and see if there are elements with the same value and adjacent.
void CheckDuplicatesSorting(int A[], int n) {
Sort(A, n);
for(int i = 0; i < n-1; i++) {
if(A[i]== A[i+1]) {
//sort the array
printf("Duplicates exist: %d", A[i]);
return;
}
printf("No duplicates in given array.");
Time Complexity: O(nlogn), for sorting (assuming nlogn sorting algorithm). Space Complexity: O(1).
Problem-3 Is there any alternative way of solving Problem-1?
Solution: Yes, using hash table. Hash tables are a simple and effective method used to implement dictionaries. Average time to search for an element is O(1), while worst-case time is O(n). Refer to Hashing chapter for more details on hashing algorithms. As an example, consider the array, A = {3,2,1,2,2,3}.
Scan the input array and insert the elements into the hash. For each inserted element, keep the counter as 1 (assume initially all entires are filled with zeros). This indicates that the corresponding element has occurred already. For the given array, the hash table will look like (after inserting the first three elements 3,2 and 1):
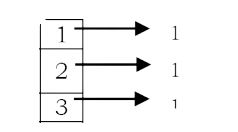
Now if we try inserting 2, since the counter value of 2 is already 1, we can say the element has appeared twice.
Time Complexity: O(n). Space Complexity: O(n).
Problem-4 Can we further improve the complexity of Problem-1 solution?
Solution: Let us assume that the array elements are positive numbers and all the elements are in the range 0 to n – 1. For each element A[i], go to the array element whose index is A[i]. That means select A[A[i]] and mark – A[A[i]] (negate the value at A[A[i]]). Continue this process until we encounter the element whose value is already negated. If one such element exists then we say duplicate elements exist in the given array. As an example, consider the array, A = {3,2,1,2,2,3}.
Initially,

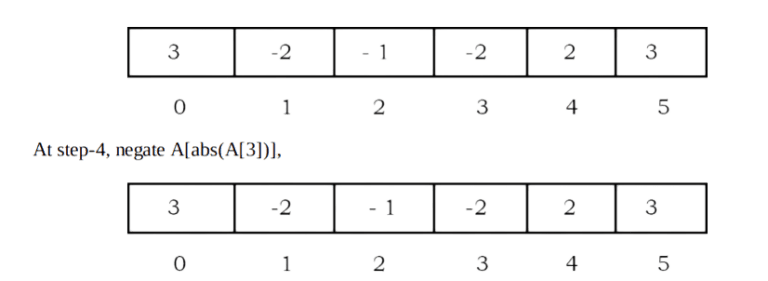
At step-4, observe that A[abs(A[3])] is already negative. That means we have encountered the same value twice
void MaxRepititions(int A[], int n) { int i= 0, max = 0, maxIndex;
for(i = 0; i < n; i++) A[A[i]%n] +=n; for(i = 0; i < n; i++) if(A[i]/n> max) {
max = A[i]/n;
maxIndex =i;
}
return maxIndex;
Time Complexity: O(n). Since only one scan is required. Space Complexity: O(1).
Notes:
• This solution does not work if the given array is read only.
• This solution will work only if all the array elements are positive.
• If the elements range is not in 0 to n – 1 then it may give exceptions.
Problem-5 Given an array of n numbers. Give an algorithm for finding the element which appears the maximum number of times in the array?
Brute Force Solution: One simple solution to this is, for each input element check whether there is any element with the same value, and for each such occurrence, increment the counter. Each time, check the current counter with the max counter and update it if this value is greater than max counter. This we can solve just by using two simple for loops.
int MaxRepititionsBrute Force(int A[], int n) { int counter =0, max=0;
for(int i = 0; i < n; i++){ counter 0;
}
}
for(int j = 0; j < n; j++) { if(A[i] == A[j])
counter++;
if(counter> max) max = counter;
return max;
Time Complexity: O(n 2 ), for two nested for loops. Space Complexity: O(1).
Problem-6 Can we improve the complexity of Problem-5 solution?
Solution: Yes. Sort the given array. After sorting, all the elements with equal values come adjacent. Now, just do another scan on this sorted array and see which element is appearing the maximum number of times. Time Complexity: O(nlogn). (for sorting). Space Complexity: O(1).
Problem-7 Is there any other way of solving Problem-5?
Solution: Yes, using hash table. For each element of the input, keep track of how many times that element appeared in the input. That means the counter value represents the number of occurrences for that element.
Time Complexity: O(n). Space Complexity: O(n).
Problem-8 or Problem-5, can we improve the time complexity? Assume that the elements’ range is 1 to n. That means all the elements are within this range only.
Solution: Yes. We can solve this problem in two scans. We cannot use the negation technique of Problem-3 for this problem because of the number of repetitions. In the first scan, instead of negating, add the value n. That means for each occurrence of an element add the array size to that element. In the second scan, check the element value by dividing it by n and return the element which gives the maximum value. The code based on this method is given below
void CheckDuplicates (int A[], int n) { for(int i = 0; i < n; i++){ if(A(abs(A[i])<0) {
}
}
printf("Duplicates exist:%d", A[i]);
return;
else A[A[i]] - - A[A[i]];
printf("No duplicates in given array.");
Notes:
• This solution does not work if the given array is read only.
• This solution will work only if the array elements are positive.
• If the elements range is not in 1 to n then it may give exceptions.
Time Complexity: O(n). Since no nested for loops are required. Space Complexity: O(1).
Problem-9 Given an array of n numbers, give an algorithm for finding the first element in the array which is repeated. For example, in the array A = {3,2,1,2,2,3}, the first repeated number is 3 (not 2). That means, we need to return the first element among the repeated elements.
Solution: We can use the brute force solution that we used for Problem-1. For each element, since it checks whether there is a duplicate for that element or not, whichever element duplicates first will be returned.
Problem-10 For Problem-9, can we use the sorting technique?
Solution: No. For proving the failed case, let us consider the following array. For example, A = {3, 2, 1, 2, 2, 3}. After sorting we get A = {1,2,2,2,3,3}. In this sorted array the first repeated element is 2 but the actual answer is 3.
Problem-11 For Problem-9, can we use hashing technique?
Solution: Yes. But the simple hashing technique which we used for Problem-3 will not work. For example, if we consider the input array as A = {3,2,1,2,3}, then the first repeated element is 3, but using our simple hashing technique we get the answer as 2. This is because 2 is coming twice before 3. Now let us change the hashing table behavior so that we get the first repeated element. Let us say, instead of storing 1 value, initially we store the position of the element in the array. As a result the hash table will look like (after inserting 3,2 and 1):
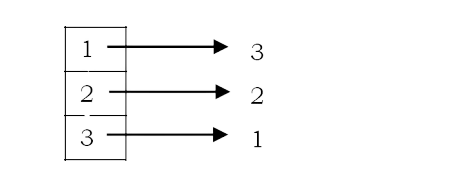
Now, if we see 2 again, we just negate the current value of 2 in the hash table. That means, we make its counter value as –2. The negative value in the hash table indicates that we have seen the same element two times. Similarly, for 3 (the next element in the input) also, we negate the current value of the hash table and finally the hash table will look like:

After processing the complete input array, scan the hash table and return the highest negative indexed value from it (i.e., –1 in our case). The highest negative value indicates that we have seen that element first (among repeated elements) and also repeating.
What if the element is repeated more than twice? In this case, just skip the element if the corresponding value i is already negative.
Problem-12 For Problem-9, can we use the technique that we used for Problem-3 (negation technique)?
Solution: No. As an example of contradiction, for the array A = {3,2,1,2,2,3} the first repeated element is 3. But with negation technique the result is 2.
Problem-13 Finding the Missing Number: We are given a list of n – 1 integers and these integers are in the range of 1 to n. There are no duplicates in the list. One of the integers is missing in the list. Given an algorithm to find the missing integer. Example: I/P: [1,2,4,6,3,7,8] O/P: 5
Brute Force Solution: One simple solution to this is, for each number in 1 to n, check whether that number is in the given array or not.
int FindMissingNumber(int A[], int n) { int i, j, found=0;
for (i = 1; i<=n;i++){ found = 0;
for (j=0; j < n; j++) if(Ali]==i) found = 1;
if(!found) return i;
}
return -1;
Time Complexity: O(n 2 ). Space Complexity: O(1).
Problem-14 For Problem-13, can we use sorting technique?
Solution: Yes. Sorting the list will give the elements in increasing order and with another scan we can find the missing number. Time Complexity: O(nlogn), for sorting. Space Complexity: O(1).
Problem-15 For Problem-13, can we use hashing technique?
Solution: Yes. Scan the input array and insert elements into the hash. For inserted elements, keep counter as 1 (assume initially all entires are filled with zeros). This indicates that the corresponding element has occurred already. Now, scan the hash table and return the element which has counter value zero.
Time Complexity: O(n). Space Complexity: O(n).
Problem-16 For Problem-13, can we improve the complexity?
Solution: Yes. We can use summation formula. 1) Get the sum of numbers, sum = n × (n + l)/2. 2) Subtract all the numbers from sum and you will get the missing number. Time Complexity: O(n), for scanning the complete array.
Problem-17 In Problem-13, if the sum of the numbers goes beyond the maximum allowed integer, then there can be integer overflow and we may not get the correct answer. Can we solve this problem?
Solution:
1) XOR all the array elements, let the result of XOR be X.
2) XOR all numbers from 1 to n, let XOR be Y.
3) XOR of X and Y gives the missing number.
int Find MissingNumber(int A[], int n) {
int i, X, Y;
for (i = 0; i < n; i++)
X Alil;
for (i = 1; i < n; i++) Y^= i;
//In fact, one variable is enough. return X^Y;
Time Complexity: O(n), for scanning the complete array. Space Complexity: O(1).
Problem-18 Find the Number Occurring an Odd Number of Times: Given an array of positive integers, all numbers occur an even number of times except one number which occurs an odd number of times. Find the number in O(n) time & constant space. Example : I/P = [1,2,3,2,3,1,3] O/P = 3
Solution: Do a bitwise XOR of all the elements. We get the number which has odd occurrences. This is because, A XOR A = 0. Time Complexity: O(n). Space Complexity: O(1).
Problem-19 Find the two repeating elements in a given array: Given an array with size, all elements of the array are in range 1 to n and also all elements occur only once except two numbers which occur twice. Find those two repeating numbers. For example: if the array is 4,2,4,5,2,3,1 with size = 7 and n = 5. This input has n + 2 = 7 elements with all elements occurring once except 2 and 4 which occur twice. So the output should be 4 2.
Solution: One simple way is to scan the complete array for each element of the input elements. That means use two loops. In the outer loop, select elements one by one and count the number of occurrences of the selected element in the inner loop. For the code below, assume that PrintRepeatedElements is called with n + 2 to indicate the size.
void PrintRepeated Elements (int A[], int size) {
for(int i=0; i< size; i++) for(int j=i+1; j< size; j++) if(A[i] == Alj]) printf("%d", A[i]);
Time Complexity: O(n 2 ). Space Complexity: O(1).
Problem-20 For Problem-19, can we improve the time complexity?
Solution: Sort the array using any comparison sorting algorithm and see if there are any elements which are contiguous with the same value.
Time Complexity: O(nlogn). Space Complexity: O(1).
Problem-21 For Problem-19, can we improve the time complexity?
Solution: Use Count Array. This solution is like using a hash table. For simplicity we can use array for storing the counts. Traverse the array once and keep track of the count of all elements in the array using a temp array count[] of size n. When we see an element whose count is already set, print it as duplicate. For the code below assume that PrintRepeatedElements is called with n+ 2 to indicate the size
void PrintRepeated Elements (int A[], int size) { int *count = (int *)calloc(sizeof(int), (size - 2)); for(int i=0; i< size; i++) { count(A[i]]++; if(count(A[i]] == 2)
printf("%d", A[i]);
Time Complexity: O(n). Space Complexity: O(n).
Problem-22 Consider Problem-19. Let us assume that the numbers are in the range 1 to n. Is there any other way of solving the problem?
Solution: Yes, by using XOR Operation. Let the repeating numbers be X and Y, if we XOR all the elements in the array and also all integers from 1 to n, then the result will be X XOR Y. The 1’s in binary representation of X XOR Y correspond to the different bits between X and Y. If the k th bit of X XOR Y is 1, we can XOR all the elements in the array and also all integers from 1 to n whose k th bits are 1. The result will be one of X and Y.
void PrintRepeated Elements (int A[], int size) {
int XOR = A[0];
int i, right_most_set_bit_no, X= 0, Y = 0;
for(i=0; i< size; i++)
XOR ^= A[i];
for(i = 1; i < n; i++)
XOR ^= i;
/* Compute XOR of all elements in A[]*/
/* Compute XOR of all elements (1, 2 ..n) */
right_most_set_bit_no = XOR & -(XOR -1); // Get the rightmost set bit in right_most_set_bit_no /* Now divide elements in two sets by comparing rightmost set */
for(i=0; i < size; i++) {
if(A[i] & right_most_set_bit_no)
X-X^ A[i];
else
Y = Y^A[i];
}
}
for(i= 1; i < n; i++){
/*XOR of first set in A[] */
/*XOR of second set in A[] */
if(i & right_most_set_bit_no) X = X^i;
else Y = Y^i;
printf("%d and %d",X, Y);
/*XOR of first set in Al] and (1, 2, ...n}*/ /*XOR of second set in A[] and (1, 2, ...n}*/
Time Complexity: O(n). Space Complexity: O(1).
Problem-23 Consider Problem-19. Let us assume that the numbers are in the range 1 to n. Is there yet other way of solving the problem?
Solution: We can solve this by creating two simple mathematical equations. Let us assume that two numbers we are going to find are X and Y. We know the sum of n numbers is n(n + l)/2 and the product is n!. Make two equations using these sum and product formulae, and get values of two unknowns using the two equations. Let the summation of all numbers in array be S and product be P and the numbers which are being repeated are X and Y.

ultiplication overflow problem with this approach.
Time Complexity: O(n). Space Complexity: O(1).
Problem-24 Similar to Problem-19, let us assume that the numbers are in the range 1 to n. Also, n – 1 elements are repeating thrice and remaining element repeated twice. Find the element which repeated twice.
Solution: If we XOR all the elements in the array and all integers from 1 to n, then all the elements which are repeated thrice will become zero. This is because, since the element is repeating thrice and XOR another time from range makes that element appear four times. As a result, the output of a XOR a XOR a XOR a = 0. It is the same case with all elements that are repeated three times.
With the same logic, for the element which repeated twice, if we XOR the input elements and also the range, then the total number of appearances for that element is 3. As a result, the output of a XOR a XOR a = a. Finally, we get the element which repeated twice.
Time Complexity: O(n). Space Complexity: O(1).
Problem-25 Given an array of n elements. Find two elements in the array such that their sum is equal to given element K.
Brute Force Solution: One simple solution to this is, for each input element, check whether there is any element whose sum is K. This we can solve just by using two simple for loops. The code for this solution can be given as:
void Brute ForceSearch[int A[], int n, int K) { for (int i = 0; i < n; i++) {
for(int j=i; j < n; j++){
if(A[i]+Ali] K) {
printf("Items Found:%d %d", i, j);
return;
}
printf("Items not found: No such elements");
Time Complexity: O(n 2 ). This is because of two nested for loops. Space Complexity: O(1).
Problem-26 For Problem-25, can we improve the time complexity?
Solution: Yes. Let us assume that we have sorted the given array. This operation takes O(nlogn). On the sorted array, maintain indices loIndex = 0 and hiIndex = n – 1 and compute A[loIndex] + A[hiIndex]. If the sum equals K, then we are done with the solution. If the sum is less than K, decrement hiIndex, if the sum is greater than K, increment loIndex.
void Search[int A[], int n, int K) { int lolndex, hilndex, sum;
Sort(A, n);
for(lolndex 0, hilndex n-1; lolndex < hilndex) { sum =A[lolndex] + A[hilndex];
}
if(sum == K) {
printf("Elements Found: %d %d", loIndex, hilndex);
return;
else if(sum < K)
loIndex = loIndex + 1;
else hilndex = hilndex - 1;
return;
Time Complexity: O(nlogn). If the given array is already sorted then the complexity is O(n). Space Complexity: O(1).
Problem-27 Does the solution of Problem-25 work even if the array is not sorted?
Solution: Yes. Since we are checking all possibilities, the algorithm ensures that we get the pair of numbers if they exist.
Problem-28 Is there any other way of solving Problem-25?
Solution: Yes, using hash table. Since our objective is to find two indexes of the array whose sum is K. Let us say those indexes are X and Y. That means, A[X] + A[Y] = K. What we need is, for each element of the input array A[X], check whether K – A[X] also exists in the input array. Now, let us simplify that searching with hash table.
Algorithm:
• For each element of the input array, insert it into the hash table. Let us say the current element is A[X].
• Before proceeding to the next element we check whether K – A[X] also exists in the hash table or not.
• Ther existence of such number indicates that we are able to find the indexes.
• Otherwise proceed to the next input element.
Time Complexity: O(n). Space Complexity: O(n). Problem-29 Given an array A of n elements. Find three indices, i,j & k such that A[i] 2 + A[j] 2 = A[k] 2? Solution:
Algorithm:
• Sort the given array in-place.
• For each array index i compute A[i] 2 and store in array.
• Search for 2 numbers in array from 0 to i – 1 which adds to A[i] similar to Problem25. This will give us the result in O(n) time. If we find such a sum, return true, otherwise continue.
void TwoElements With MinSum(int A[], int n) { int i, j, min_sum, sum, min_i, min_j, inv_count = 0;
if(n< 2) {
}
printf("Invalid Input");
return;
/* Initialization of values */
min_i = 0; min_j=1;
min_sum =A[0] + A[1];
for(i=0; i<n-1; i++)
for(j=i+1; j < n; j++) {
sum =A[i] + A[j];
if(abs(min_sum)> abs(sum)) {
min_sum = sum;
min_i=i;
min_j-j;
printf(" The two elements are %d and %d", arr[min_i], arr[min_j]);
Time Complexity: Time for sorting + n × (Time for finding the sum) = O(nlogn) + n × O(n)= n 2 . Space Complexity: O(1).
Problem-30 Two elements whose sum is closest to zero. Given an array with both positive and negative numbers, find the two elements such that their sum is closest to zero. For the below array, algorithm should give -80 and 85. Example: 1 60 – 10 70 – 80 85
Brute Force Solution: For each element, find the sum with every other element in the array and compare sums. Finally, return the minimum sum.
Sort(A); // Sort the input array for (int i=0; i < n; i++) A[i] = A[i]*A[i]; for (i=n; i > 0; i--) { res = false;
if(res) {
//Problem-11/12 Solution
}
Time complexity: O(n 2 ). Space Complexity: O(1).
Problem-31 Can we improve the time complexity of Problem-30?
Solution: Use Sorting.
Algorithm:
1. Sort all the elements of the given input array.
2. Maintain two indexes, one at the beginning (i = 0) and the other at the ending (j = n – 1). Also, maintain two variables to keep track of the smallest positive sum closest to zero and the smallest negative sum closest to zero.
3. While i < j:
a. If the current pair sum is > zero and < postiveClosest then update the postiveClosest. Decrement j.
b. If the current pair sum is < zero and > negativeClosest then update the negativeClosest. Increment i.
c. Else, print the pair
void Search[int Al[], int n, int data) {
Sort(A, n);
for(int k = 0; k < n; k++) {
for(int i=k+1,j=n-1; i<j; ) {
}
if(A[k]+A[i]+A[j] == data) {
printf("Items Found:%d %d %d", i, j, k); return;
else if(A[k] + A[i] + Ali] < data) i = i + 1;
else j-j-1;
}
return;
Time Complexity: O(nlogn), for sorting. Space Complexity: O(1).
Problem-32 Given an array of n elements. Find three elements in the array such that their sum is equal to given element K?
Brute Force Solution: The default solution to this is, for each pair of input elements check whether there is any element whose sum is K. This we can solve just by using three simple for loops. The code for this solution can be given as:
void Brute ForceSearch[int A[], int n, int data) {
for (int i = 0; i < n; i++) { for(int j=i+1; j < n; j++) {
{
for(int kj+1; k < n; k++) if(A[i]+Aj]+A[k]== data) {
printf("Items Found: %d %d %d", i, j, k);
return;
}
}
}
printf("Items not found: No such elements");
Time Complexity: O(n 3 ), for three nested for loops. Space Complexity: O(1).
Problem-33 Does the solution of Problem-32 work even if the array is not sorted?
Solution: Yes. Since we are checking all possibilities, the algorithm ensures that we can find three numbers whose sum is K if they exist.
Problem-34 Can we use sorting technique for solving Problem-32?
Solution: Yes.
void TwoElements With MinSum(int A[], int n) {
int i=0,j=n-1, temp, postiveClosest = INT_MAX, negativeClosest = INT_MIN;
Sort(A, n); while(i<j) {
temp Ali] + Ali];
if(temp > 0) {
if (temp < postive Closest)
postiveClosest = temp;
j-;
}
else if (temp < 0) {
if (temp> negativeClosest)
negativeClosest = temp;
i++;
}
else printf("Closest Sum: %d ", A[i] + A[j]);
return (abs(negativeClosest)> postiveClosest: postiveClosest: negativeClosest);
Time Complexity: Time for sorting + Time for searching in sorted list = O(nlogn) + O(n 2 ) ≈ O(n 2 ). This is because of two nested for loops. Space Complexity: O(1).
Problem-35 Can we use hashing technique for solving Problem-32?
Solution: Yes. Since our objective is to find three indexes of the array whose sum is K. Let us say those indexes are X,Y and Z. That means, A[X] + A[Y] + A[Z] = K. Let us assume that we have kept all possible sums along with their pairs in hash table. That means the key to hash table is K – A[X] and values for K – A[X] are all possible pairs of input whose sum is if – A[X].
Algorithm:
• Before starting the search, insert all possible sums with pairs of elements into the hash table.
• For each element of the input array, insert into the hash table. Let us say the current element is A[X].
• Check whether there exists a hash entry in the table with key: K – A[X].
• If such element exists then scan the element pairs of K – A[X] and return all possible pairs by including A[X] also.
• If no such element exists (with K – A[X] as key) then go to next element.
Time Complexity: The time for storing all possible pairs in Hash table + searching = O(n 2 ) + O(n 2 ) ≈ O(n 2 ). Space Complexity: O(n).
Problem-36 Given an array of n integers, the 3 – sum problem is to find three integers whose sum is closest to zero.
Solution: This is the same as that of Problem-32 with K value is zero.
Problem-37 Let A be an array of n distinct integers. Suppose A has the following property: there exists an index 1 ≤ k ≤ n such that A[l],…, A[k] is an increasing sequence and A[k + 1],…, A[n] is a decreasing sequence. Design and analyze an efficient algorithm for finding k.
Similar question: Let us assume that the given array is sorted but starts with negative numbers and ends with positive numbers [such functions are called monotonically increasing functions]. In this array find the starting index of the positive numbers. Assume that we know the length of the input array. Design a O(logn) algorithm.
Solution: Let us use a variant of the binary search.
int Search (int A[], int n, int first, int last) { int mid, first 0, last = n-1; while(first <= last) {
// if the current array has size 1 if(first == last)
return A[first];
// if the current array has size 2
else if(first == last-1)
return max(A[first), A[last]);
// if the current array has size 3 or more
else {
mid=first+ (last-first)/2;
if(A[mid-1] < A[mid] && A[mid] > A[mid+1]) return A[mid];
else if(A[mid-1]< A[mid] && A[mid] < A[mid+1]) first = mid+1;
else if(A[mid-1]> A[mid] && A[mid] > A[mid+1])
else
} // end of else
} //end of while
last = mid-1;
return INT_MIN;
The recursion equation is T(n) = 2T(n/2) + c. Using master theorem, we get O(logn).
Problem-38 If we don’t know n, how do we solve the Problem-37?
Solution: Repeatedly compute A[1],A[2],A[4],A[8],A[16] and so on, until we find a value of n such that A[n] > 0.
Time Complexity: O(logn), since we are moving at the rate of 2. Refer to Introduction to Analysis of Algorithms chapter for details on this.
Problem-39 Given an input array of size unknown with all 1’s in the beginning and 0’s in the end. Find the index in the array from where 0’s start. Consider there are millions of 1’s and 0’s in the array. E.g. array contents 1111111……..1100000……..0000000.
Solution: This problem is almost similar to Problem-38. Check the bits at the rate of 2 Kwhere k = 0,1,2 …. Since we are moving at the rate of 2, the complexity is O(logn).
Problem-40 Given a sorted array of n integers that has been rotated an unknown number of times, give a O(logn) algorithm that finds an element in the array. Example: Find 5 in array (15 16 19 20 25 1 3 4 5 7 10 14) Output: 8 (the index of 5 in the array)
Solution: Let us assume that the given array is A[]and use the solution of Problem-37 with an extension. The function below FindPivot returns the k value (let us assume that this function returns the index instead of the value). Find the pivot point, divide the array into two sub-arrays and call binary search. The main idea for finding the pivot point is – for a sorted (in increasing order) and pivoted array, the pivot element is the only element for which the next element to it is smaller than it. Using the above criteria and the binary search methodology we can get pivot element in O(logn) time.
Algorithm:
1) Find out the pivot point and divide the array into two sub-arrays.
2) Now call binary search for one of the two sub-arrays.
a. if the element is greater than the first element then search in left subarray.
b. else search in right subarray.
3) If element is found in selected sub-array, then return index else return –1.
int Find Pivot(int A[], int start, int finish) { if(finish - start == 0) return start;
else if(start finish -1) { if(A[start] >= A[finish])
}
return start;
else
return finish;
}
else {
mid 1= start + (finish-start)/2; if(A(start] >= A[mid])
return Find Pivot(A, start, mid);
else
return FindPivot(A, mid, finish);
}
int Search(int A[], int n, int x) {
int pivot FindPivot(A, 0, n-1);
if(A[pivot] == x)
return pivot;
if(A[pivot] <= x)
return BinarySearch(A, 0, pivot-1, x); else return BinarySearch(A, pivot+1, n-1, x);
int Binary Search (int A[], int low, int high, int x) {
if(high >= low) {
int mid low (high-low)/2;
if(x == A[mid])
return mid;
if(x > A[mid])
return BinarySearch(A, (mid + 1), high, x);
else return BinarySearch(A, low, (mid -1), x);
}
return -1;
//-1 if element is not found
Time complexity: O(logn).
Problem-41 For Problem-40, can we solve with recursion?
Solution: Yes.
int Binary SearchRotated (int All, int start, int finish, int data) { int mid start + (finish - start) / 2; if(start > finish) return -1;
}
if(data == A[mid])
return mid;
else if(A[start] <= A[mid]) {
// start half is in sorted order.
if(data = A[start] && data < A[mid])
return Binary Search Rotated (A, start, mid - 1, data); else return BinarySearchRotated (A, mid + 1, finish, data);
else{ // A[mid] <= A[finish], finish half is in sorted order. if(data > A[mid] && data <= A[finish])
return Binary SearchRotated (A, mid + 1, finish, data); else return BinarySearchRotated (A, start, mid- 1, data);
Time complexity: O(logn).
Problem-42 Bitonic search: An array is bitonic if it is comprised of an increasing sequence of integers followed immediately by a decreasing sequence of integers. Given a bitonic array A of n distinct integers, describe how to determine whether a given integer is in the array in O(logn) steps.
Solution: The solution is the same as that for Problem-37. Problem-43 Yet, other way of framing Problem-37. Let A[] be an array that starts out increasing, reaches a maximum, and then decreases. Design an O(logn) algorithm to find the index of the maximum value.
Problem-44 Give an O(nlogn) algorithm for computing the median of a sequence of n integers.
Solution: Sort and return element at .
Problem-45 Given two sorted lists of size m and n, find median of all elements in O(log (m + n)) time.
Solution: Refer to Divide and Conquer chapter.
Problem-46 Given a sorted array A of n elements, possibly with duplicates, find the index of the first occurrence of a number in O(logn) time.
Solution: To find the first occurrence of a number we need to check for the following condition.
Return the position if any one of the following is true:

int BinarySearchLast Occurrence(int A[], int low, int high, int data) {
}
int mid;
if(high >= low) {
mid low (high-low) / 2;
if((mid == high && A[mid] == data) || (A[mid] == data && A[mid + 1] > data))
return mid;
// Give preference to right half of the array
else if(A[mid] <= data)
return Binary SearchLastOccurrence (A, mid + 1, high, data); else return BinarySearchLastOccurrence (A, low, mod - 1, data);
return -1;
Time Complexity: O(logn).
Problem-47 Given a sorted array A of n elements, possibly with duplicates. Find the index of the last occurrence of a number in O(logn) time.
Solution: To find the last occurrence of a number we need to check for the following condition.
Return the position if any one of the following is true:
int LinearSearchCount(int A[], int n, int data) {
int count = 0;
for (int i = 0; i < n; i++) if(A[i] == data)
return count;
count++;
Time Complexity: O(logn).
Problem-48 Given a sorted array of n elements, possibly with duplicates. Find the number of occurrences of a number.
Brute Force Solution: Do a linear search of the array and increment count as and when we find the element data in the array
int Binary Search FirstOccurrence(int A[], int low, int high, int data) {
int mid;
if(high >= low) {
mid-low + (high-low) / 2;
if(mid == low && A[mid] == data) || (A[mid] == data && A[mid - 1] < data)) return mid;
// Give preference to left half of the array
else if(A[mid] >= data)
else
return -1;
return BinarySearchFirstOccurrence (A, low, mid - 1, data); return Binary Search FirstOccurrence (A, mid + 1, high, data);
Time Complexity: O(n).
Problem-49 Can we improve the time complexity of Problem-48?
Solution: Yes. We can solve this by using one binary search call followed by another small scan.
Algorithm:
• Do a binary search for the data in the array. Let us assume its position is K.
• Now traverse towards the left from K and count the number of occurrences of data. Let this count be leftCount.
• Similarly, traverse towards right and count the number of occurrences of data. Let this count be rightCount.
• Total number of occurrences = leftCount + 1 + rightCount Time Complexity – O(logn + S) where 5 is the number of occurrences of data.
Problem-50 Is there any alternative way of solving Problem-48?
Solution:
Algorithm:
• Find first occurrence of data and call its index as firstOccurrence (for algorithm refer to Problem-46)
• Find last occurrence of data and call its index as lastOccurrence (for algorithm refer to Problem-47)
• Return lastOccurrence – firstOccurrence + 1 Time Complexity = O(logn + logn) = O(logn).
Problem-51 What is the next number in the sequence 1,11,21 and why?
Solution: Read the given number loudly. This is just a fun problem.

So the answer is: the next number is the representation of the previous number by reading it loudly.
Problem-52 Finding second smallest number efficiently.
Solution: We can construct a heap of the given elements using up just less than n comparisons (Refer to the Priority Queues chapter for the algorithm). Then we find the second smallest using logn comparisons for the GetMax() operation. Overall, we get n + logn + constant.
Problem-53 Is there any other solution for Problem-52?
Solution: Alternatively, split the n numbers into groups of 2, perform n/2 comparisons successively to find the largest, using a tournament-like method. The first round will yield the maximum in n – 1 comparisons. The second round will be performed on the winners of the first round and the ones that the maximum popped. This will yield logn – 1 comparison for a total of n + logn – 2. The above solution is called the tournament problem.
Problem-54 An element is a majority if it appears more than n/2 times. Give an algorithm takes an array of n element as argument and identifies a majority (if it exists).
Solution: The basic solution is to have two loops and keep track of the maximum count for all different elements. If the maximum count becomes greater than n/2, then break the loops and return the element having maximum count. If maximum count doesn’t become more than n/2, then the majority element doesn’t exist.
Time Complexity: O(n 2 ). Space Complexity: O(1).
Problem-55 Can we improve Problem-54 time complexity to O(nlogn)?
Solution: Using binary search we can achieve this. Node of the Binary Search Tree (used in this approach) will be as follows
int MajorityNum(int[] A, int n) { int count = 0, element = -1; for(int i=0; i < n; i++) {
// If the counter is 0 then set the current candidate to majority num and set the counter to 1. if(count == 0) {
}
}
element - A[i]; count = 1;
else if(element == A[i]) {
else{
// Increment counter If the counter is not 0 and element is same as current candidate. count++;
// Decrement counter If the counter is not 0 and element is different from current candidate. count--;
}
return element;
Insert elements in BST one by one and if an element is already present then increment the count of the node. At any stage, if the count of a node becomes more than n/2, then return. This method works well for the cases where n/2 +1 occurrences of the majority element are present at the start of the array, for example {1,1,1,1,1,2,3, and 4}.
Time Complexity: If a binary search tree is used then worst time complexity will be O(n 2 ). If a balanced-binary-search tree is used then O(nlogn). Space Complexity: O(n).
Problem-56 Is there any other of achieving O(nlogn) complexity for Problem-54?
Solution: Sort the input array and scan the sorted array to find the majority element.
Time Complexity: O(nlogn). Space Complexity: O(1).
Problem-57 Can we improve the complexity for Problem-54?
Solution: If an element occurs more than n/2 times in A then it must be the median of A. But, the reverse is not true, so once the median is found, we must check to see how many times it occurs in A. We can use linear selection which takes O(n) time (for algorithm, refer to Selection Algorithms chapter).
int CheckMajority(int A[], in n)
1) Use linear selection to find the median m of A.
2) Do one more pass through A and count the number of occurrences of m.
a. If m occurs more than n/2 times then return true;
b. Otherwise return false. }
Problem-58 Is there any other way of solving Problem-54?
Solution: Since only one element is repeating, we can use a simple scan of the input array by keeping track of the count for the elements. If the count is 0, then we can assume that the element visited for the first time otherwise that the resultant element.
struct TreeNode { int element;
int count;
}BST;
struct TreeNode "left;
struct TreeNode "right;
Time Complexity: O(n). Space Complexity: O(1).
Problem-59 Given an array of 2n elements of which n elements are the same and the remaining n elements are all different. Find the majority element.
Solution: The repeated elements will occupy half the array. No matter what arrangement it is, only one of the below will be true:
• All duplicate elements will be at a relative distance of 2 from each other. Ex:n, 1, n, 100, n, 54, n…
• At least two duplicate elements will be next to each other. Ex: n,n, 1,100, n, 54, n,…. n, 1,n,n,n,54,100… 1,100,54, n.n.n.n….
In worst case, we will need two passes over the array:
• First Pass: compare A[i] and A[i + 1]
• Second Pass: compare A[i] and A[i + 2]
Something will match and that’s your element. This will cost O(n) in time and O(1) in space.
Problem-60 Given an array with 2n + 1 integer elements, n elements appear twice in arbitrary places in the array and a single integer appears only once somewhere inside. Find the lonely integer with O(n) operations and O(1) extra memory.
Solution: Except for one element, all elements are repeated. We know that A XOR A = 0. Based on this if we XOR all the input elements then we get the remaining element.
int Solution(int* A) { int i, res;
for (i= res= 0; i < 2n+1; i++)
Λ
res = res res ^ A[i];
return res;
Time Complexity: O(n). Space Complexity: O(1).
Problem-61 Throwing eggs from an n-story building: Suppose we have an n story building and a number of eggs. Also assume that an egg breaks if it is thrown from floor F or higher, and will not break otherwise. Devise a strategy to determine floor F, while breaking O(logn) eggs.
Solution: Refer to Divide and Conquer chapter.
Problem-62 Local minimum of an array: Given an array A of n distinct integers, design an O(logn) algorithm to find a local minimum: an index i such that A[i – 1] < A[i] < A[i + 1].
Solution: Check the middle value A[n/2], and two neighbors A[n/2 – 1] and A[n/2 + 1]. If A[n/2] is local minimum, stop; otherwise search in half with smaller neighbor.
Problem-63 Give an n × n array of elements such that each row is in ascending order and each column is in ascending order, devise an O(n) algorithm to determine if a given element x is in the array. You may assume all elements in the n × n array are distinct.
Solution: Let us assume that the given matrix is A[n][n]. Start with the last row, first column [or first row, last column]. If the element we are searching for is greater than the element at A[1][n], then the first column can be eliminated. If the search element is less than the element at A[1][n], then the last row can be completely eliminated. Once the first column or the last row is eliminated, start the process again with the left-bottom end of the remaining array. In this algorithm, there would be maximum n elements that the search element would be compared with.
Time Complexity: O(n). This is because we will traverse at most 2n points. Space Complexity: O(1).
Problem-64 Given an n × n array a of n 2 numbers, give an O(n) algorithm to find a pair of indices i and j such that A[i][j] < A[i + 1][j].A[i][j] < A[i][j + 1],A[i][j] < A[i – 1][j], and A[i][j] < A[i][j – 1].
Solution: This problem is the same as Problem-63
Problem-65 Given n × n matrix, and in each row all 1’s are followed by 0’s. Find the row with the maximum number of 0’s.
Solution: Start with first row, last column. If the element is 0 then move to the previous column in the same row and at the same time increase the counter to indicate the maximum number of 0’s. If the element is 1 then move to the next row in the the same column. Repeat this process until your reach last row, first column.
Time Complexity: O(2n) ≈ O(n) (similar to Problem-63).
Problem-66 Given an input array of size unknown, with all numbers in the beginning and special symbols in the end. Find the index in the array from where the special symbols start.
Solution: Refer to Divide and Conquer chapter.
Problem-67 Separate even and odd numbers: Given an array A[], write a function that segregates even and odd numbers. The functions should put all even numbers first, and then odd numbers. Example: Input = {12,34,45,9,8,90,3} Output = {12,34,90,8,9,45,3} Note: In the output, the order of numbers can be changed, i.e., in the above example 34 can come before 12, and 3 can come before 9.
Solution: The problem is very similar to Separate 0’s and 1’s (Problem-68) in an array, and both problems are variations of the famous Dutch national flag problem.
Algorithm: The logic is similar to Quick sort.
1) Initialize two index variables left and right: left = 0, right = n – 1
2) Keep incrementing the left index until you see an odd number.
3) Keep decrementing the right index until youe see an even number.
4) If left < right then swap A[left] and A[right]
void Sorting012sDutch FlagProblem(int A[], int n){
int low=0,mid-0,high-n-1;
while(mid <=high){ switch(A(mid)){
case 0:
case 1:
case 2:
swap(A[low],A[mid]);
low++; mid++;
break;
mid++;
break;
swap(A[mid].A[high]);
high--; break;
Time Complexity: O(n).
Problem-68 The following is another way of structuring Problem-67, but with a slight difference. Separate 0’s and 1’s in an array: We are given an array of 0’s and 1’s in random order. Separate 0’s on the left side and 1’s on the right side of the array. Traverse the array only once. Input array = [0,1,0,1,0,0,1,1,1,0] Output array = [0,0,0,0,0,1,1,1,1,1]
Solution: Counting 0’s or 1’s 1. Count the number of 0’s. Let the count be C. 2. Once we have the count, put C 0’s at the beginning and 1’s at the remaining n- C positions in the array.
Time Complexity: O(n). This solution scans the array two times.
Problem-69 Can we solve Problem-68 in one scan?
Solution: Yes. Use two indexes to traverse: Maintain two indexes. Initialize the first index left as 0 and the second index right as n – 1. Do the following while left < right: 1) Keep the incrementing index left while there are Os in it 2) Keep the decrementing index right while there are Is in it 3) If left < right then exchange A[left] and A[right]
void DutchNationalFlag(int A[], int n) { int left = 0, right = n-1; while(left < right) {
// Increment left index while we see 0 at left while(A[left]%2== 0 && left < right) left++;
// Decrement right index while we see 1 at right while(A[right]%2== 1 && left < right)
right--;
if(left < right) {
// Swap A[left] and A[right] swap(&A[left], &A[right]);
left++;
right--;
}
Time Complexity: O(n). Space Complexity: O(1).
Problem-70 Sort an array of 0’s, 1’s and 2’s [or R’s, G’s and B’s]: Given an array A[] consisting of 0’s, 1’s and 2’s, give an algorithm for sorting A[].The algorithm should put all 0’s first, then all 1’s and finally all 2’s at the end. Example Input = {0,1,1,0,1,2,1,2,0,0,0,1}, Output = {0,0,0,0,0,1,1,1,1,1,2,2}
Solution:
//Function to put all Os on left and all 1s on right void Separate0and1 (int A[], int n) {
/* Initialize left and right indexes */ int left 0, right n-1; while(left < right){
/* Increment left index while we see 0 at left */ while(A[left] == 0 && left < right)
left++;
/* Decrement right index while we see 1 at right*/ while(A[right] 1 && left < right)
right-;
/* If left is smaller than right then there is a 1 at left and a 0 at right. Swap A[left] and A[right]*/
if(left < right){
A[left] = 0;
A[right] = 1;
left++;
right-;
Time Complexity: O(n). Space Complexity: O(1).
Problem-71 Maximum difference between two elements: Given an array A[] of integers, find out the difference between any two elements such that the larger element appears after the smaller number in A[]. Examples: If array is [2,3,10,6,4,8,1] then returned value should be 8 (Difference between 10 and 2). If array is [ 7,9,5,6,3,2 ] then the returned value should be 2 (Difference between 7 and 9)
Solution: Refer to Divide and Conquer chapter.
Problem-72 Given an array of 101 elements. Out of 101 elements, 25 elements are repeated twice, 12 elements are repeated 4 times, and one element is repeated 3 times. Find the element which repeated 3 times in O(1).
solution: Before solving this problem, let us consider the following XOR operation property: a XOR a = 0. That means, if we apply the XOR on the same elements then the result is 0. Algorithm:
• XOR all the elements of the given array and assume the result is A.
• After this operation, 2 occurrences of the number which appeared 3 times becomes 0 and one occurrence remains the same.
• The 12 elements that are appearing 4 times become 0.
• The 25 elements that are appearing 2 times become 0.
• So just XOR’ing all the elements gives the result.
Time Complexity: O(n), because we are doing only one scan. Space Complexity: O(1).
Problem-73 Given a number n, give an algorithm for finding the number of trailing zeros in n!.
Solution
int maxIndexDiff(int A[], int n){
int maxDiff = -1; int i, j;
for (i=0; i < n; ++i){
for (j-n-1;j>i; --){
if(A[i]> A[i] && maxDiff < (j-i)) maxDiff-j-i;
}
return maxDiff;
Time Complexity: O(logn).
Problem-74 Given an array of 2n integers in the following format a1 a2 a3 …an b1 b2 b3 …bn. Shuffle the array to a1 b1 a2 b2 a3 b3 … an bn without any extra memory.
Solution: A brute force solution involves two nested loops to rotate the elements in the second half of the array to the left. The first loop runs n times to cover all elements in the second half of the array. The second loop rotates the elements to the left. Note that the start index in the second loop depends on which element we are rotating and the end index depends on how many positions we need to move to the left.
int NumberOfTrailingZerosInNumber(int n) { int i, count = 0; if(n< 0) return -1;
for (i= 5; n /i> 0; i = 5) count += n / i;
return count;
Time Complexity: O(n 2 ).
Problem-75 Can we improve Problem-74 solution?
Solution: Refer to the Divide and Conquer chapter. A better solution of time complexity O(nlogn) can be achieved using the Divide and Concur technique. Let us look at an example
1. Start with the array: a1 a2 a3 a4 b1 b2 b3 b4
2. Split the array into two halves: a1 a2 a3 a4 : b1 b2 b3 b4
3. Exchange elements around the center: exchange a3 a4 with b1 b2 and you get: a1 a.2 b1 b2 a3 a4 b3 b4
4. Split a1 a2 b1 b2 into a1 a2 : b1 b2. Then split a3 a4 b3 b4 into a3 a4 : b3 b4
5. Exchange elements around the center for each subarray you get: a1 b1 a2 b2 and a3 b3 a4 b4
Note that this solution only handles the case when n = 2 i where i = 0,1,2,3, etc. In our example n = 2 2 = 4 which makes it easy to recursively split the array into two halves. The basic idea behind swapping elements around the center before calling the recursive function is to produce smaller size problems. A solution with linear time complexity may be achieved if the elements are of a specific nature. For example, if you can calculate the new position of the element using the value of the element itself. This is nothing but a hashing technique.
Problem-76 Given an array A[], find the maximum j – i such that A[j] > A[i]. For example, Input: {34, 8, 10, 3, 2, 80, 30, 33, 1} and Output: 6 (j = 7, i = 1).
Solution: Brute Force Approach: Run two loops. In the outer loop, pick elements one by one from the left. In the inner loop, compare the picked element with the elements starting from the right side. Stop the inner loop when you see an element greater than the picked element and keep updating the maximum j – i so far.
void ShuffleArray() { int n = 4;
int Al]=(1,3,5,7,2,4,6,8};
for (int i=0, q-1, kn; i < n; i++, k++, q++) { for (int j k;ji+q; j--) {
int tmp = Alj-1]; Aj-1] - Ab]; A[j] = tmp;
}
}
for (int i=0; i < 2 n; i++)
printf("%d", A[i]);
Time Complexity: O(n 2 ). Space Complexity: O(1).
Problem-77 Can we improve the complexity of Problem-76?
Solution: To solve this problem, we need to get two optimum indexes of A[]: left index i and right index j. For an element A[i], we do not need to consider A[i] for the left index if there is an element smaller than A[i] on the left side of A[i]. Similarly, if there is a greater element on the right side of A[j] then we do not need to consider this j for the right index.
So we construct two auxiliary Arrays LeftMins[] and RightMaxs[] such that LeftMins[i] holds the smallest element on the left side of A[i] including A[i], and RightMaxs[j] holds the greatest element on the right side of A[j] including A[j]. After constructing these two auxiliary arrays, we traverse both these arrays from left to right.
While traversing LeftMins[] and RightMaxs[], if we see that LeftMins[i] is greater than RightMaxs[j], then we must move ahead in LeftMins[] (or do i++) because all elements on the left of LeftMins[i] are greater than or equal to LeftMins[i]. Otherwise we must move ahead in RightMaxs[j] to look for a greater y – i value.
int maxIndexDifflint A[], int n){ int maxDiff, i, j;
int *LeftMins (int *)malloc(sizeof(int)*n);
int *RightMaxs (int *)malloc(sizeof(int)*n); LeftMins[0] = A[0];
for (i = 1; i < n; ++i)
LeftMins[i]= min(A[i], LeftMins[i-1]); RightMaxs[n-1] A[n-1];
=
for (in-2;j>= 0; --j)
RightMaxs[j]=max(A[j], RightMaxs[j+1]); i=0,j=0, maxDiff = -1;
while (j < n && i < n){
if (LeftMins[i] < RightMaxs[j]){ maxDiff max(maxDiff, j-i); j-j+1;
else
i=i+1;
}
return maxDiff;
Time Complexity: O(n). Space Complexity: O(n).
Problem-78 Given an array of elements, how do you check whether the list is pairwise sorted or not? A list is considered pairwise sorted if each successive pair of numbers is in sorted (non-decreasing) order.
Solution:
void frequencyCounter(int A[], int n){ int pos = 0; while(pos<n){
}
int expectedPos A[pos] - 1;
if(A[pos] > 0 && A(expectedPos] > 0){ swap(A[pos], A[expectedPos]); A[expected Pos] = -1;
else if(A[pos]>0){
A[expected Pos]--; A[pos++] = 0;
}
else{
}
pos ++;
for(int i = 0; i < n; ++i){
printf("%d frequency is %d\n", i + 1,abs(A[i]);
int main(int argc, char* argv[]){
int A[]=(10, 10, 9, 4, 7, 6, 5, 2, 3, 2, 1); frequencyCounter(A, sizeof(A)/ sizeof(A[0])); return 0;
Time Complexity: O(n). Space Complexity: O(1).
Problem-79 Given an array of n elements, how do you print the frequencies of elements without using extra space. Assume all elements are positive, editable and less than n.
Solution: Use negation technique.
int checkPairwise Sorted(int A[], int n) { if (n == 0 || n == 1) return 1;
for (int i=0; i<n-1; i+=2){
}
if (A[i]> A[i+1])
return 0;
return 1;
Array should have numbers in the range [1, n] (where n is the size of the array). The if condition (A[pos] > 0 && A[expectedPos] > 0) means that both the numbers at indices pos and expectedPos are actual numbers in the array but not their frequencies. So we will swap them so that the number at the index pos will go to the position where it should have been if the numbers 1, 2, 3, …., n are kept in 0, 1, 2, …, n – 1 indices. In the above example input array, initially pos = 0, so 10 at index 0 will go to index 9 after the swap. As this is the first occurrence of 10, make it to -1. Note that we are storing the frequencies as negative numbers to differentiate between actual numbers and frequencies.
The else if condition (A[pos] > 0) means A[pos] is a number and A[expectedPos] is its frequency without including the occurrence of A[pos]. So increment the frequency by 1 (that is decrement by 1 in terms of negative numbers). As we count its occurrence we need to move to next pos, so pos + +, but before moving to that next position we should make the frequency of the number pos + 1 which corresponds to index pos of zero, since such a number has not yet occurred. The final else part means the current index pos already has the frequency of the number pos + 1, so move to the next pos, hence pos + +.
Time Complexity: O(n). Space Complexity: O(1).
Problem-80 Which is faster and by how much, a linear search of only 1000 elements on a 5- GHz computer or a binary search of 1 million elements on a 1-GHz computer. Assume that the execution of each instruction on the 5-GHz computer is five times faster than on the 1- GHz computer and that each iteration of the linear search algorithm is twice as fast as each iteration of the binary search algorithm.
Solution: A binary search of 1 million elements would require or about 20 iterations at most (i.e., worst case). A linear search of 1000 elements would require 500 iretations on the average (i.e., going halfway through the array). Therefore, binary search would be faster (in terms of iterations) than linear search. However, since linear search iterations are twice as fast, binary search would be or about 12 times faster than linear search overall, on the same machine. Since we run them on different machines, where an instruction on the 5-GhZ machine is 5 times faster than an instruction on a 1-GHz machine, binary search would be or about 2 times faster than linear search! The key idea is that software improvements can make an algorithm run much faster without having to use more powerful software.

