5.1 What is a Stack?
A stack is a simple data structure used for storing data (similar to Linked Lists). In a stack, the order in which the data arrives is important. A pile of plates in a cafeteria is a good example of a stack. The plates are added to the stack as they are cleaned and they are placed on the top. When a
plate, is required it is taken from the top of the stack. The first plate placed on the stack is the last one to be used.
Definition: A stack is an ordered list in which insertion and deletion are done at one end, called top. The last element inserted is the first one to be deleted. Hence, it is called the Last in First out (LIFO) or First in Last out (FILO) list.
Special names are given to the two changes that can be made to a stack. When an element is inserted in a stack, the concept is called push, and when a element is removed from the stack, the concept is called pop. Trying to pop out an empty stack is called underflow and trying to push an element in a full stack is called overflow. Generally, we treat them as exceptions. As an example, consider the snapshots of the stack

5.2 How Stacks are used
Consider a working day in the office. Let us assume a developer is working on a long-term project. The manager then gives the developer a new task which is more important. The developer puts the long-term project aside and begins work on the new task. The phone rings, and this is the highest priority as it must be answered immediately. The developer pushes the present task into the pending tray and answers the phone.
When the call is complete the task that was abandoned to answer the phone is retrieved from the pending tray and work progresses. To take another call, it may have to be handled in the same manner, but eventually the new task will be finished, and the developer can draw the long-term project from the pending tray and continue with that.
5.3 Stack ADT
The following operations make a stack an ADT. For simplicity, assume the data is an integer type.
Main stack operations
• Push (int data): Inserts data onto stack.
• int Pop(): Removes and returns the last inserted element from the stack
Auxiliary stack operations
• int Top(): Returns the last inserted element without removing it.
• int Size(): Returns the number of elements stored in the stack.
• int IsEmptyStack(): Indicates whether any elements are stored in the stack or not. • int IsFullStack(): Indicates whether the stack is full or not.
Exceptions
Attempting the execution of an operation may sometimes cause an error condition, called an exception. Exceptions are said to be “thrown” by an operation that cannot be executed. In the Stack ADT, operations pop and top cannot be performed if the stack is empty. Attempting the execution of pop (top) on an empty stack throws an exception. Trying to push an element in a full stack throws an exceptio
5.4 Applications
Following are some of the applications in which stacks play an important role.
Direct applications
• Balancing of symbol
• Infix-to-postfix conversion
• Evaluation of postfix expression
• Implementing function calls (including recursion)
• Finding of spans (finding spans in stock markets, refer to Problems section)
• Page-visited history in a Web browser [Back Buttons]
• Undo sequence in a text editor
• Matching Tags in HTMLand XML
Indirect applications
• Auxiliary data structure for other algorithms (Example: Tree traversal algorithms)
• Component of other data structures (Example: Simulating queues, refer Queues chapter)
5.5 Implementation
There are many ways of implementing stack ADT; below are the commonly used methods.
• Simple array based implementation
• Dynamic array based implementation
• Linked lists implementation
Simple Array Implementation
This implementation of stack ADT uses an array. In the array, we add elements from left to right and use a variable to keep track of the index of the top element.
The array storing the stack elements may become full. A push operation will then throw a full
stack exception. Similarly, if we try deleting an element from an empty stack it will throw stack
empty exception

#define MAXSIZE 10 struct ArrayStack ( int top;
int capacity;
int *array;
struct ArrayStack *CreateStack() {
struct ArrayStack *S = malloc(sizeof(struct ArrayStack)); if(!S)
return NULL;
S-capacity MAXSIZE;
S-top = -1;
S-array malloc(S-capacity * sizeof(int)); if(!S-array)
return NULL;
return S;
int IsEmptyStack(struct ArrayStack *S) {
}
return (S-top == -1); // if the condition is true then 1 is returned else 0 is returned
int IsFullStack(struct ArrayStack *S){
}
//if the condition is true then 1 is returned else 0 is returned
return (S-top S-capacity - 1);
void Push(struct ArrayStack *S, int data){
/S-top capacity-1 indicates that the stack is full*/
if(IsFullStack(S))
printf("Stack Overflow");
else /*Increasing the 'top' by 1 and storing the value at 'top' position*/ Sarray[++Stop]= data;
int Pop(struct ArrayStack *S){
/*S-top-1 indicates empty stack*/
if(IsEmptyStack(S)){
}
printf("Stack is Empty");
return INT_MIN;;
else / Removing element from 'top' of the array and reducing 'top' by 1*/ return (S- array(S-top--]);
void DeleteStack(struct DynArrayStack *S){
if(S){
if(S-array)
free(S-array);
free(S);
Performance & Limitations
Performance
Let n be the number of elements in the stack. The complexities of stack operations with this representation can be given as:

Limitations
The maximum size of the stack must first be defined and it cannot be changed. Trying to push a new element into a full stack causes an implementation-specific exception.
Dynamic Array Implementation
First, let’s consider how we implemented a simple array based stack. We took one index variable top which points to the index of the most recently inserted element in the stack. To insert (or push) an element, we increment top index and then place the new element at that index.
Similarly, to delete (or pop) an element we take the element at top index and then decrement the top index. We represent an empty queue with top value equal to –1. The issue that still needs to be resolved is what we do when all the slots in the fixed size array stack are occupied?
First try: What if we increment the size of the array by 1 every time the stack is full?
• Push(); increase size of S[] by 1
• Pop(): decrease size of S[] by 1
Problems with this approach?
This way of incrementing the array size is too expensive. Let us see the reason for this. For example, at n = 1, to push an element create a new array of size 2 and copy all the old array elements to the new array, and at the end add the new element. At n = 2, to push an element create a new array of size 3 and copy all the old array elements to the new array, and at the end add the new element.
Similarly, at n = n – 1, if we want to push an element create a new array of size n and copy all the old array elements to the new array and at the end add the new element. After n push operations the total time T(n) (number of copy operations) is proportional to 1 + 2 + … + n ≈ O(n 2 ).
Alternative Approach: Repeated Doubling
Let us improve the complexity by using the array doubling technique. If the array is full, create a new array of twice the size, and copy the items. With this approach, pushing n items takes time proportional to n (not n 2 ).
For simplicity, let us assume that initially we started with n = 1 and moved up to n = 32. That means, we do the doubling at 1,2,4,8,16. The other way of analyzing the same approach is: at n = 1, if we want to add (push) an element, double the current size of the array and copy all the elements of the old array to the new array.
At n = 1, we do 1 copy operation, at n = 2, we do 2 copy operations, and at n = 4, we do 4 copy operations and so on. By the time we reach n = 32, the total number of copy operations is 1+2 + 4 + 8+16 = 31 which is approximately equal to 2n value (32). If we observe carefully, we are doing the doubling operation logn times. Now, let us generalize the discussion. For n push operations we double the array size logn times. That means, we will have logn terms in the expression below. The total time T(n) of a series of n push operations is proportional to
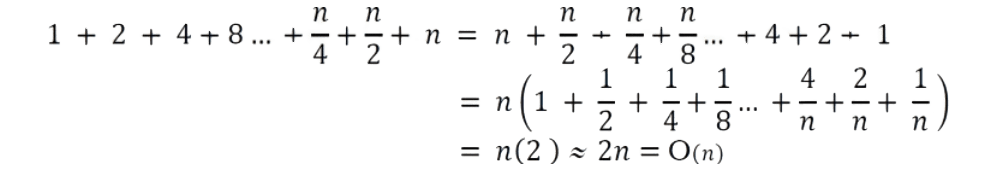
T(n) is O(n) and the amortized time of a push operation is O(1) .
struct DynArrayStack{ int top; int capacity; int "array;
struct DynArrayStack *CreateStack(){
struct DynArrayStack *S= malloc(sizeof(struct DynArrayStack));
if(!S)
return NULL;
S-capacity = 1;
S-top = -1;
S-array malloc(S-capacity sizeof(int)); // allocate an array of size 1 initially
if(!S-array)
return NULL;
return S;
int IsFullStack(struct DynArrayStack *S){
}
return (Stop S-capacity-1);
void DoubleStack(struct DynArrayStack *S){
S-capacity *= 2;
S-array = realloc(S-array, S-capacity sizeof(int));
void Push(struct DynArrayStack *S, int x){ // No overflow in this implementation if(IsFullStack(S))
}
DoubleStack(S);
S-array[++Stop] = x;
int IsEmptyStack(struct DynArrayStack *S){
}
return S→top == -1;
int Top(struct DynArrayStack *S){
}
if(IsEmptyStack(S))
return INT_MIN;
return S-array[S-top];
int Pop(struct DynArrayStack *S){
}
if(IsEmptyStack(S))
return INT_MIN;
return S-array[S-top--];
void DeleteStack(struct DynArrayStack *S){
if(S)
}
if(S-array)
free(S-array);
free(S);
Performance
Let n be the number of elements in the stack. The complexities for operations with this representation can be given as:

Note: Too many doublings may cause memory overflow exception.
Linked List Implementation
The other way of implementing stacks is by using Linked lists. Push operation is implemented by inserting element at the beginning of the list. Pop operation is implemented by deleting the node from the beginning (the header/top node)
}
struct ListNode int data;
struct ListNode *next;
struct Stack *CreateStack(){
return NULL;
void Push(struct Stack **top, int data){
}
struct Stack *temp;
temp = malloc(sizeof(struct Stack));
if(!temp)
return NULL;
temp-data = data;
temp->next = 'top; *top = temp;
int IsEmptyStack(struct Stack "top){
}
return top == NULL;
int Pop(struct Stack **top){
}
int data;
struct Stack *temp; if(IsEmptyStack(top))
return INT_MIN;
temp = "top;
"top = "top-next;
data = temp-data;
free(temp);
return data;
int Top(struct Stack * top){
}
if(IsEmptyStack(top)) return INT_MIN; return top-next-data;
void DeleteStack(struct Stack **top){
struct Stack *temp, *p;
p = "top;
while(p-next) {
}
=
temp = p->next; p-next temp-next; free(temp);
free(p):
Performance
Let n be the number of elements in the stack. The complexities for operations with this representation can be given as:

5.6 Comparison of Implementations
Comparing Incremental Strategy and Doubling Strategy
We compare the incremental strategy and doubling strategy by analyzing the total time T(n) needed to perform a series of n push operations. We start with an empty stack represented by an array of size 1.
We call amortized time of a push operation is the average time taken by a push over the series of operations, that is, T(n)/n.
Incremental Strategy
The amortized time (average time per operation) of a push operation is O(n) [O(n 2 )/n].
Doubling Strategy
In this method, the amortized time of a push operation is O(1) [O(n)/n]
Note: For analysis, refer to the Implementation section.
Comparing Array Implementation and Linked List Implementation
Array Implementation
• Operations take constant time
• Expensive doubling operation every once in a while.
• Any sequence of n operations (starting from empty stack) – “amortized” bound takes time proportional to n.
Linked List Implementation
• Grows and shrinks gracefully.
• Every operation takes constant time O(1).
• Every operation uses extra space and time to deal with references
5.7 Stacks: Problems & Solutions
Problem-1 Discuss how stacks can be used for checking balancing of symbols.
Solution: Stacks can be used to check whether the given expression has balanced symbols. This algorithm is very useful in compilers. Each time the parser reads one character at a time. If the character is an opening delimiter such as (, {, or [- then it is written to the stack. When a closing delimiter is encountered like ), }, or ]-the stack is popped.
The opening and closing delimiters are then compared. If they match, the parsing of the string continues. If they do not match, the parser indicates that there is an error on the line. A linear-time O(n) algorithm based on stack can be given as:
Algorithm:
a) Create a stack.
b) while (end of input is not reached) {
1) If the character read is not a symbol to be balanced, ignore it.
2) If the character is an opening symbol like (, [, {, push it onto the stack
3) If it is a closing symbol like ),],}, then if the stack is empty report an error. Otherwise pop the stack.
4) If the symbol popped is not the corresponding opening symbol, report an error. }
c) At end of input, if the stack is not empty report an error
Examples:

For tracing the algorithm let us assume that the input is: () (() [()])
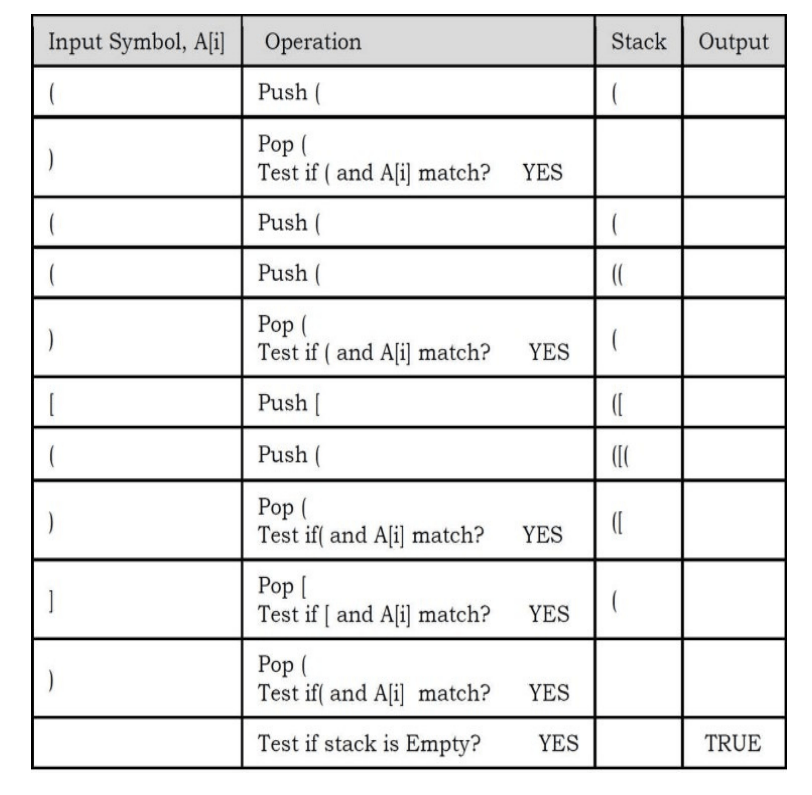
Time Complexity: O(n). Since we are scanning the input only once. Space Complexity: O(n) [for stack].
Problem-2 Discuss infix to postfix conversion algorithm using stack.
Solution: Before discussing the algorithm, first let us see the definitions of infix, prefix and postfix expressions.
Infix: An infix expression is a single letter, or an operator, proceeded by one infix string and followed by another Infix string.
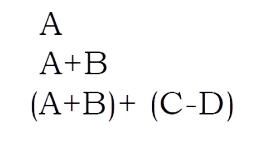
Prefix: A prefix expression is a single letter, or an operator, followed by two prefix strings. Every prefix string longer than a single variable contains an operator, first operand and second operand.
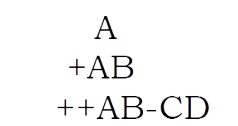
Postfix: A postfix expression (also called Reverse Polish Notation) is a single letter or an
operator, preceded by two postfix strings. Every postfix string longer than a single variable
contains first and second operands followed by an operator.
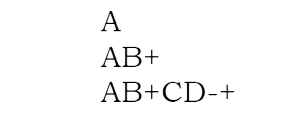
Prefix and postfix notions are methods of writing mathematical expressions without parenthesis. Time to evaluate a postfix and prefix expression is O(n), where n is the number of elements in the array.

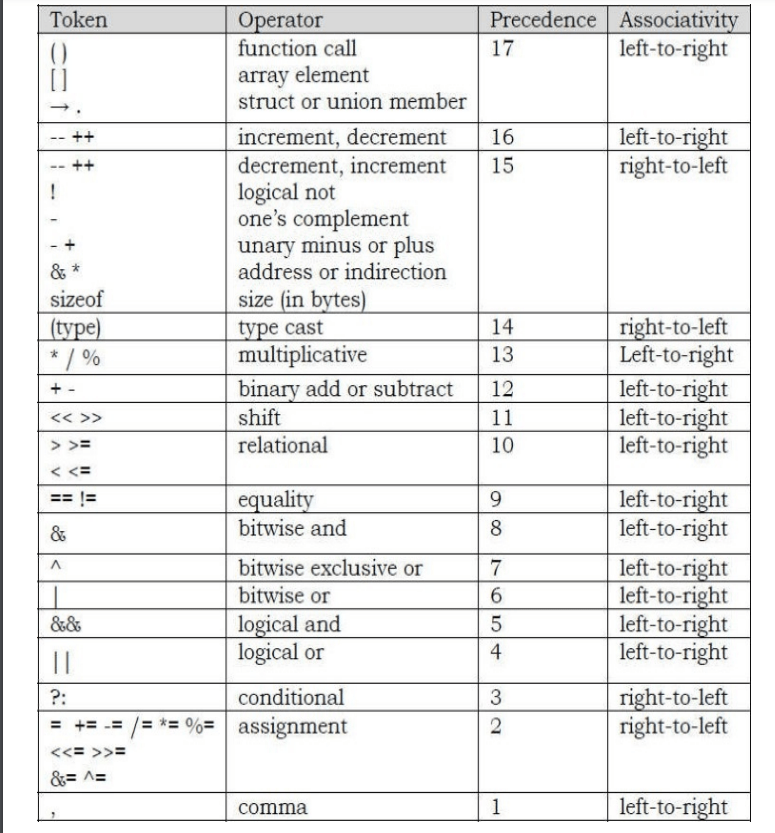
Now, let us focus on the algorithm. In infix expressions, the operator precedence is implicit unless we use parentheses. Therefore, for the infix to postfix conversion algorithm we have to define the operator precedence (or priority) inside the algorithm.
The table shows the precedence and their associativity (order of evaluation) among operators.

Important Properties
• Let us consider the infix expression 2 + 3*4 and its postfix equivalent 234*+. Notice that between infix and postfix the order of the numbers (or operands) is unchanged. It is 2 3 4 in both cases. But the order of the operators * and + is affected in the two expressions.
• Only one stack is enough to convert an infix expression to postfix expression. The stack that we use in the algorithm will be used to change the order of operators from infix to postfix. The stack we use will only contain operators and the open parentheses symbol ‘(‘.
Postfix expressions do not contain parentheses. We shall not output the parentheses in the postfix output.
Algorithm:
a) Create a stack
b) for each character t in the input stream}
c) pop and output tokens until the stack is empty
For better understanding let us trace out an example: A * B- (C + D) + E

Problem-3 Discuss postfix evaluation using stacks?
Solution:
Algorithm:
1 Scan the Postfix string from left to right.
2 Initialize an empty stack.
3 Repeat steps 4 and 5 till all the characters are scanned.
4 If the scanned character is an operand, push it onto the stack.
5 If the scanned character is an operator, and if the operator is a unary operator, then pop an element from the stack. If the operator is a binary operator, then pop twoelements from the stack. After popping the elements, apply the operator to those popped elements. Let the result of this operation be retVal onto the stack.
6 After all characters are scanned, we will have only one element in the stack.
7 Return top of the stack as result.
Example: Let us see how the above-mentioned algorithm works using an example. Assume thatthe postfix string is 123*+5-.
Initially the stack is empty. Now, the first three characters scanned are 1, 2 and 3, which are
operands. They will be pushed into the stack in that order

The next character scanned is “*”, which is an operator. Thus, we pop the top two elements from the stack and perform the “*” operation with the two operands. The second operand will be the first element that is popped

The value of the expression (2*3) that has been evaluated (6) is pushed into the stack.

The next character scanned is “+”, which is an operator. Thus, we pop the top two elements from the stack and perform the “+” operation with the two operands. The second operand will be the first element that is popped

The value of the expression (1+6) that has been evaluated (7) is pushed into the stack.

The next character scanned is “5”, which is added to the stack.
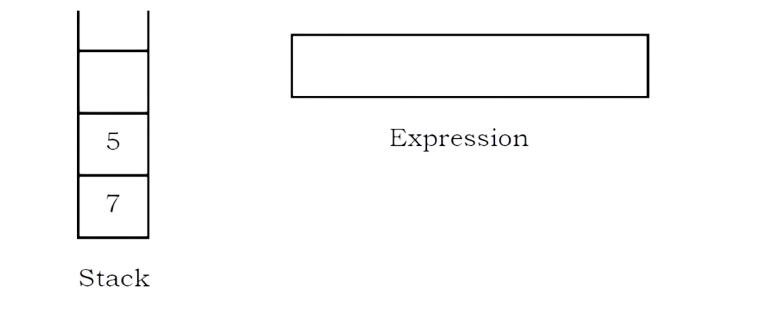
The next character scanned is “-”, which is an operator. Thus, we pop the top two elements from the stack and perform the “-” operation with the two operands. The second operand will be the first element that is popped.
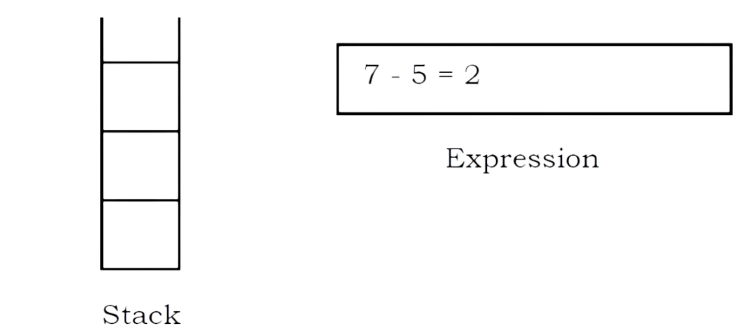
The next character scanned is “-”, which is an operator. Thus, we pop the top two elements from the stack and perform the “-” operation with the two operands. The second operand will be the first element that is popped.

Now, since all the characters are scanned, the remaining element in the stack (there will be only one element in the stack) will be returned. End result
• Postfix String : 123*+5-
• Result : 2
problem-4 Can we evaluate the infix expression with stacks in one pass?
Solution: Using 2 stacks we can evaluate an infix expression in 1 pass without converting to postfix
Algorithm:
1) Create an empty operator stack
2) Create an empty operand stack
3) For each token in the input string
a. Get the next token in the infix string
b. If next token is an operand, place it on the operand stack
c. If next token is an operator
i. Evaluate the operator (next op)
4) While operator stack is not empty, pop operator and operands (left and right),evaluate left operator right and push result onto operand stack
5) Pop result from operator stack
Problem-5 How to design a stack such that Get Minimum( ) should be O(1)?
Solution: Take an auxiliary stack that maintains the minimum of all values in the stack. Also, assume that each element of the stack is less than its below elements. For simplicity let us call the auxiliary stack min stack.
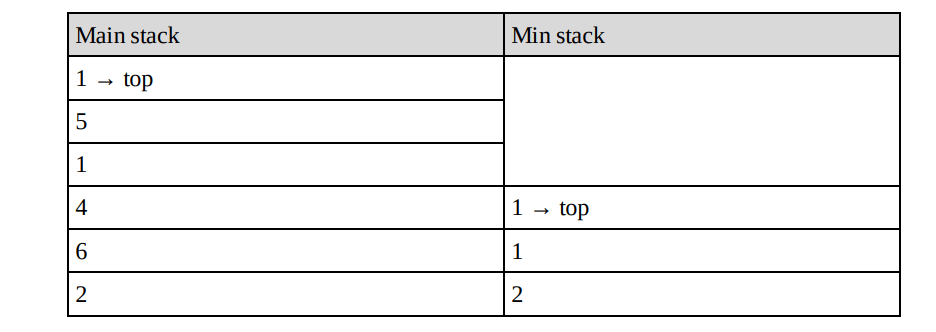
When we pop the main stack, pop the min stack too. When we push the main stack, push either the new element or the current minimum, whichever is lower. At any point, if we want to get the minimum, then we just need to return the top element from the min stack. Let us take an example and trace it out. Initially let us assume that we have pushed 2, 6, 4, 1 and 5. Based on the abovementioned algorithm the min stack will look like:

After popping twice we get:

Based on the discussion above, now let us code the push, pop and GetMinimum() operations.
}
struct AdvancedStack{
struct Stack elementStack; struct Stack minStack;
void Push(struct AdvancedStack *S, int data){
Push (S-elementStack, data);
if(IsEmptyStack(S-minStack) | | Top(S-minStack) >= data) Push (S-minStack, data);
else Push (S-minStack, Top(S→minStack));
int Pop(struct AdvancedStack *S){
}
int temp;
if(IsEmptyStack(S-elementStack)) return -1;
temp = Pop (S-elementStack);
Pop (S-minStack);
return temp;
int GetMinimum(struct AdvancedStack *S){
return Top(S-minStack);
}
struct AdvancedStack *CreateAdvancedStack(){
struct AdvancedStack *S = (struct AdvancedStack *)malloc(sizeof(struct AdvancedStack));
if(!S)
return NULL;
S-elementStack = CreateStack();
S-minStackCreateStack();
return
Time complexity: O(1). Space complexity: O(n) [for Min stack]. This algorithm has much better space usage if we rarely get a “new minimum or equal”.
Problem-6 For Proble m-5is it possible to improve the space complexity?
Solution: Yes. The main problem of the previous approach is, for each push operation we are
pushing the element on to min stack also (either the new element or existing minimum element).
That means, we are pushing the duplicate minimum elements on to the stack.
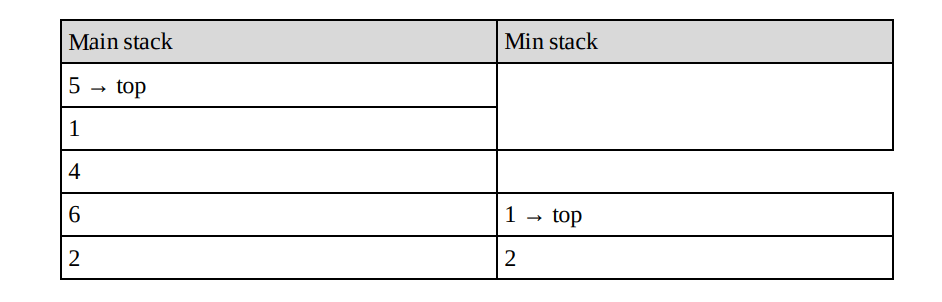
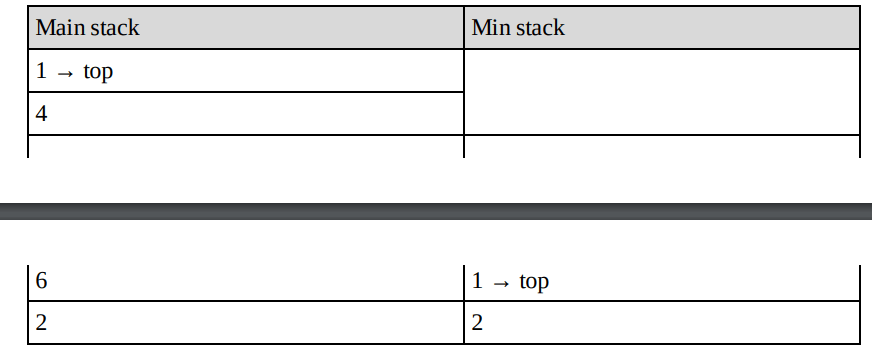
Now, let us change the algorithm to improve the space complexity. We still have the min stack, but we only pop from it when the value we pop from the main stack is equal to the one on the min stack. We only push to the min stack when the value being pushed onto the main stack is less than or equal to the current min value. In this modified algorithm also, if we want to get the minimum then we just need to return the top element from the min stack. For example, taking the original version and pushing 1 again, we’d get:
Popping from the above pops from both stacks because 1 == 1, leaving:
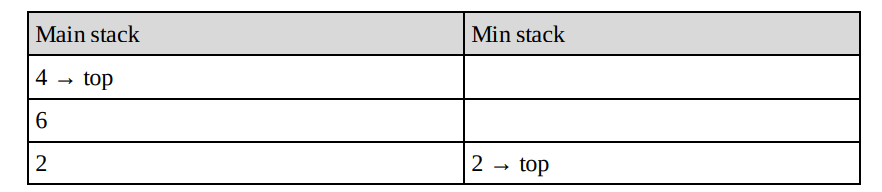
Popping again only pops from the main stack, because 5 > 1:
Popping again pops both stacks because 1 == 1:
Note: The difference is only in push & pop operations.
struct AdvancedStack{ struct Stack elementStack; struct Stack minStack;
void Push(struct AdvancedStack *S, int data){
Push (S-elementStack, data);
if(IsEmptyStack(S-minStack) || Top(S-minStack) >= data) Push (S-minStack, data);
int Pop/struct AdvancedStack *S
int temp;
if(IsEmptyStack(S-elementStack)) return -1;
=
temp Top (S-elementStack);
if(Top(SminStack) == Pop(S-elementStack)) Pop (S-minStack);
return temp;
int GetMinimum(struct AdvancedStack *S){
return Top(S-minStack);
struct AdvancedStack * AdvancedStack(){
struct AdvancedStack *S= (struct AdvancedStack) malloc (sizeof (struct AdvancedStack));
if(!S)
return NULL;
S-elementStackCreateStack();
S-minStackCreateStack();
return S;
}
Time complexity: O(1). Space complexity: O(n) [for Min stack]. But this algorithm has much better space usage if we rarely get a “new minimum or equal”.
Problem-7 For a given array with n symbols how many stack permutations are possible?
Solution: The number of stack permutations with n symbols is represented by Catalan number and we will discuss this in the Dynamic Programming chapter.
Problem-8 Given an array of characters formed with a’s and b’s. The string is marked with special character X which represents the middle of the list (for example: ababa…ababXbabab baaa). Check whether the string is palindrome.
Solution: This is one of the simplest algorithms. What we do is, start two indexes, one at the
beginning of the string and the other at the end of the string. Each time compare whether the values
at both the indexes are the same or not. If the values are not the same then we say that the given
string is not a palindrome.
If the values are the same then increment the left index and decrement the right index. Continue this process until both the indexes meet at the middle (at X) or if the string is not palindrome.
int IsPalindrome(char *A){ int i=0, j = strlen(A)-1; while(i<j && A[i] == A[j]) { i++;
}
j-;
if(i<j){
}
printf("Not a Palindrome"); return 0;
else {
printf("Palindrome");
return 1;
}
}
Time Complexity: O(n). Space Complexity: O(1).
Problem-9 For Problem-8, if the input is in singly linked list then how do we check whether the list elements form a palindrome (That means, moving backward is not possible).
Solution: Refer Linked Lists chapter.
Problem-10 Can we solve Problem-8 using stacks?
Solution: Yes.
Algorithm
• Traverse the list till we encounter X as input element.
• During the traversal push all the elements (until X) on to the stack.
• For the second half of the list, compare each element’s content with top of the stack. If they are the same then pop the stack and go to the next element in the input list.
• If they are not the same then the given string is not a palindrome.
• Continue this process until the stack is empty or the string is not a palindrome
int IsPalindrome(char *A){ int i=0;
struct Stack S CreateStack();
while(A[i] != 'X') {
i++;
Push(S, A[i]);
i++;
while(A[i]) {
if(IsEmptyStack(S) ||A[i] != Pop(S)) { printf("Not a Palindrome");
}
itt;
return 0;
}
return IsEmptyStack(S);
Time Complexity: O(n). Space Complexity: O(n/2) ≈ O(n)
Problem-11 Given a stack, how to reverse the elements of the stack using only stack operations (push & pop)?
Solution:
Algorithm:
• First pop all the elements of the stack till it becomes empty.
• For each upward step in recursion, insert the element at the bottom of the stack.
void ReverseStack(struct Stack *S){ int data;
}
if(IsEmptyStack(S)) return;
data = Pop(S); ReverseStack(S); InsertAtBottom(S, data);
void InsertAtBottom(struct Stack *S, int data){
int temp; if(IsEmptyStack(S)) { Push(S, data);
}
return;
temp = Pop(S);
InsertAtBottom(S, data); Push(S, temp);
Problem-12 Show how to implement one queue efficiently using two stacks. Analyze the running time of the queue operations.
Solution: Refer Queues chapter
Problem-13 Show how to implement one stack efficiently using two queues. Analyze the running time of the stack operations.
Solution: Refer Queues chapter
Problem-14 How do we implement two stacks using only one array? Our stack routines should not indicate an exception unless every slot in the array is used?
Solution:

Algorithm:
• Start two indexes one at the left end and the other at the right end.
• The left index simulates the first stack and the right index simulates the second stack.
• If we want to push an element into the first stack then put the element at the left index.
• Similarly, if we want to push an element into the second stack then put the element at the right index.
• The first stack grows towards the right, and the second stack grows towards the left.
Time Complexity of push and pop for both stacks is O(1). Space Complexity is O(1).
Problem-15 3 stacks in one array: How to implement 3 stacks in one array?
Solution: For this problem, there could be other ways of solving it. Given below is one
possibility and it works as long as there is an empty space in the array.

To implement 3 stacks we keep the following information.
• The index of the first stack (Topi): this indicates the size of the first stack.
• The index of the second stack (Top2): this indicates the size of the second stack.
• Starting index of the third stack (base address of third stack).
• Top index of the third stack.
Now, let us define the push and pop operations for this implementation.
Pushing:
• For pushing on to the first stack, we need to see if adding a new element causes it to bump into the third stack. If so, try to shift the third stack upwards. Insert the new element at (start1 + Top1).
• For pushing to the second stack, we need to see if adding a new element causes it to bump into the third stack. If so, try to shift the third stack downward. Insert the new element at (start2 – Top2).
• When pushing to the third stack, see if it bumps into the second stack. If so, try to shift the third stack downward and try pushing again. Insert the new element at (start3 + Top3). Time Complexity: O(n). Since we may need to adjust the third stack. Space Complexity: O(1).
Popping: For popping, we don’t need to shift, just decrement the size of the appropriate stack. Time Complexity: O(1). Space Complexity: O(1).
Problem-16 For Problem-15, is there any other way implementing the middle stack?
Solution: Yes. When either the left stack (which grows to the right) or the right stack (which grows to the left) bumps into the middle stack, we need to shift the entire middle stack to make room. The same happens if a push on the middle stack causes it to bump into the right stack.
To solve the above-mentioned problem (number of shifts) what we can do is: alternating pushes can be added at alternating sides of the middle list (For example, even elements are pushed to the left, odd elements are pushed to the right). This would keep the middle stack balanced in the center of the array but it would still need to be shifted when it bumps into the left or right stack, whether by growing on its own or by the growth of a neighboring stack. We can optimize the initial locations of the three stacks if they grow/shrink at different rates and if they have different average sizes. For example, suppose one stack doesn’t change much. If we put it at the left, then the middle stack will eventually get pushed against it and leave a gap between the middle and right stacks, which grow toward each other. If they collide, then it’s likely we’ve run out of space in the array. There is no change in the time complexity but the average number of shifts will get reduced.
Problem-17 Multiple (m) stacks in one array: Similar to Problem-15, what if we want to implement m stacks in one array?
Solution: Let us assume that array indexes are from 1 to n. Similar to the discussion in Problem15, to implement m stacks in one array, we divide the array into m parts (as shown below). The size of each part is .n\m
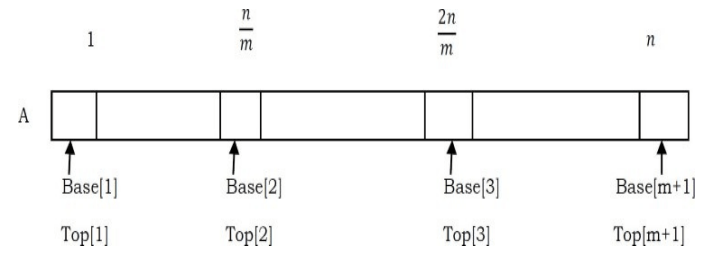
From the above representation we can see that, first stack is starting at index 1 (starting index is stored in Base[l]), second stack is starting at index n\m (starting index is stored in Base[2]), third stack is starting at index 2n\m (starting index is stored in Base[3]), and so on. Similar to Base array, let us assume that Top array stores the top indexes for each of the stack. Consider the following terminology for the discussion.
• Top[i], for 1 ≤ i ≤ m will point to the topmost element of the stack i.
• If Base[i] == Top[i], then we can say the stack i is empty.
• If Top[i] == Base[i+1], then we can say the stack i is full.
Initially Base[i] = Top[i] n\m = (i – 1), for 1 ≤ i ≤ m.
• The stack grows from Base[i]+1 to Base[i+1]
Pushing on to i th stack:
1) For pushing on to the i th stack, we check whether the top of i th stack is pointing to Base[i+1] (this case defines that i th stack is full). That means, we need to see if adding a new element causes it to bump into the i + 1 th stack. If so, try to shift the stacks from i + 1 th stack to mth stack toward the right. Insert the new element at (Base[i] + Top[i]).
2) If right shifting is not possible then try shifting the stacks from 1 to i –1 th stack toward the left.
3) If both of them are not possible then we can say that all stacks are full.
void Push(int StackID, int data) { if(Top[i] == Base[i+1])
Print ith Stack is full and does the necessary action (shifting);
Top[i] = Top[i]+1; A[Top[i]] = data;
Time Complexity: O(n). Since we may need to adjust the stacks. Space Complexity: O(1).
Popping from i th stack: For popping, we don’t need to shift, just decrement the size of the
appropriate stack. The only case to check is stack empty case.
int Pop(int StackID) { if(Top[i] == Base[i])
Print it Stack is empty;
return A[Top[i]--;
Time Complexity: O(1). Space Complexity: O(1).
Problem-18 Consider an empty stack of integers. Let the numbers 1,2,3,4,5,6 be pushed on to this stack in the order they appear from left to right. Let 5 indicate a push and X indicate a pop operation. Can they be permuted in to the order 325641(output) and order 154623?
Solution: SSSXXSSXSXXX outputs 325641. 154623 cannot be output as 2 is pushed much
before 3 so can appear only after 3 is output.
Problem-19 Earlier in this chapter, we discussed that for dynamic array implementation of
stacks, the ‘repeated doubling’ approach is used. For the same problem, what is the
complexity if we create a new array whose size is n + if instead of doubling?
Solution: Let us assume that the initial stack size is 0. For simplicity let us assume that K = 10.For inserting the element we create a new array whose size is 0 + 10 = 10. Similarly, after 10elements we again create a new array whose size is 10 + 10 = 20 and this process continues atvalues: 30,40 … That means, for a given n value, we are creating the new arrays at :n\10,n\20,n\30,n\40…The total number of copy operations is:

If we are performing n push operations, the cost per operation is O(logn).
Problem-20 Given a string containing n S’s and n X’s where 5 indicates a push operation and X indicates a pop operation, and with the stack initially empty, formulate a rule to check whether a given string 5 of operations is admissible or not?
Solution: Given a string of length 2n, we wish to check whether the given string of operations is permissible or not with respect to its functioning on a stack. The only restricted operation is pop whose prior requirement is that the stack should not be empty. So while traversing the string from left to right, prior to any pop the stack shouldn’t be empty, which means the number of S’s is always greater than or equal to that of X’s. Hence the condition is at any stage of processing of the string, the number of push operations (S) should be greater than the number of pop operations (X)
Problem-21 Suppose there are two singly linked lists which intersect at some point and become a single linked list. The head or start pointers of both the lists are known, but the intersecting node is not known. Also, the number of nodes in each of the lists before they intersect are unknown and both lists may have a different number. List1 may have n nodes before it reaches the intersection point and List2 may have m nodes before it reaches the intersection point where m and n may be m = n,m < n or m > n. Can we find the merging point using stacks?
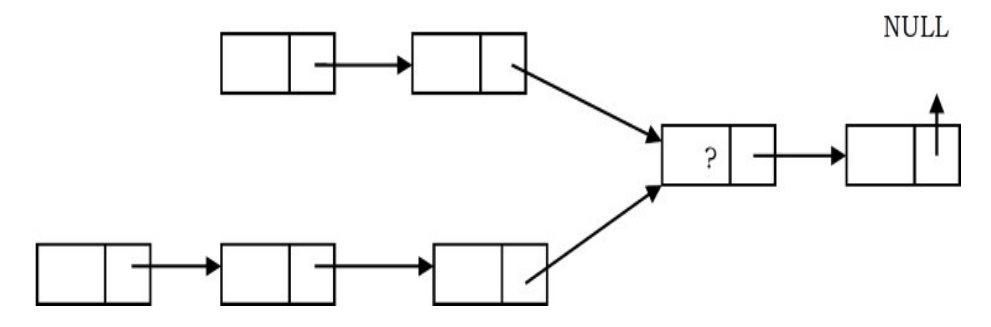
Solution: Yes. For algorithm refer to Linked Lists chapter.
Problem-22 Finding Spans: Given an array A, the span S[i] of A[i] is the maximum number of consecutive elements A[j] immediately preceding A[i] and such that A[j] < A[i]? Other way of asking: Given an array A of integers, find the maximum of j – i subjected to the constraint of A[i] < A[j].
Solution:
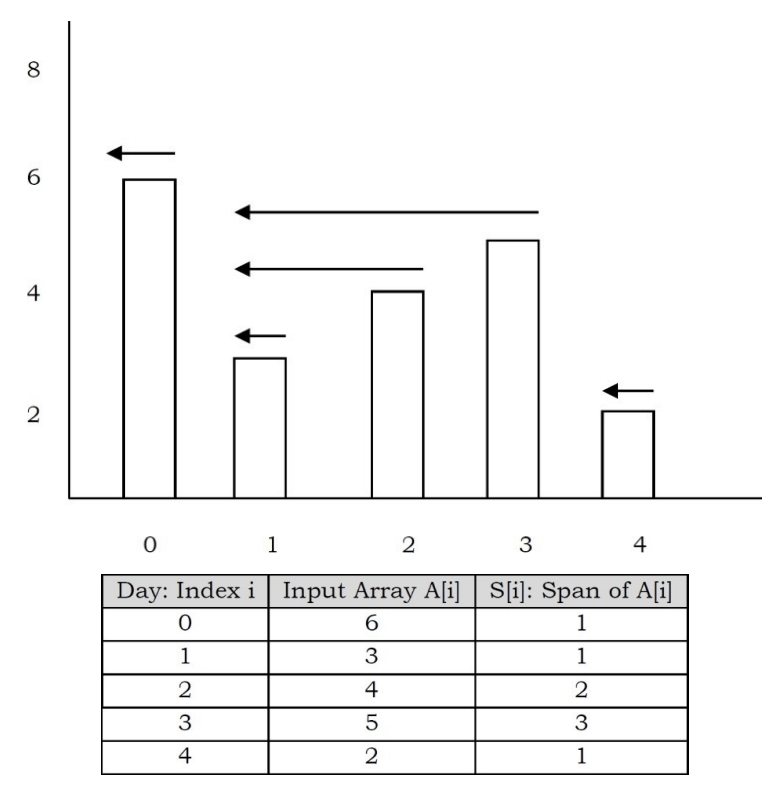
This is a very common problem in stock markets to find the peaks. Spans are used in financial analysis (E.g., stock at 52-week high). The span of a stock price on a certain day, i, is the maximum number of consecutive days (up to the current day) the price of the stock has been less than or equal to its price on i.
As an example, let us consider the table and the corresponding spans diagram. In the figure the arrows indicate the length of the spans. Now, let us concentrate on the algorithm for finding the spans. One simple way is, each day, check how many contiguous days have a stock price that is less than the current price
Algorithm: FindingSpans(int A[], int n) {
//Input: array A of n integers, Output: array S of spans of A
int i, j, S[n]; //new array of n integers;
n
while (j <= i && A[i]> A[i-j]) 1+2+...+ (n-1)
j=j;+1 1+2+...+ (n-1)
for (i=0; i < n; i++) { n
return S; 1
Problem-23 Can we improve the complexity of Problem-22?
Solution: From the example above, we can see that span S[i] on day i can be easily calculated if we know the closest day preceding i, such that the price is greater on that day than the price on day i. Let us call such a day as P. If such a day exists then the span is now defined as S[i] = i – P
Algorithm: FindingSpans (int A[], int n) { struct Stack *D = CreateStack();
int P;
for (int i=0 i< n; i++) {
while (!IsEmptyStack(D) && A[i]> A[Top(D)]) {
}
return S;
Pop(D);
if(IsEmptyStack(D)) P-1;
else P = Top(D); Si]=i-P; Push(D, i);
Time Complexity: Each index of the array is pushed into the stack exactly once and also popped from the stack at most once. The statements in the while loop are executed at most n times. Even though the algorithm has nested loops, the complexity is O(n) as the inner loop is executing only n times during the course of the algorithm (trace out an example and see how many times the inner loop becomes successful). Space Complexity: O(n) [for stack].
Problem-24 Largest rectangle under histogram: A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. For simplicity, assume that the rectangles have equal widths but may have different heights. For example, the figure on the left shows a histogram that consists of rectangles with the heights 3,2,5,6,1,4,4, measured in units where 1 is the width of the rectangles. Here our problem is: given an array with heights of rectangles (assuming width is 1), we need to find the largest rectangle possible. For the given example, the largest rectangle is the shared part.
Solution: A straightforward answer is to go to each bar in the histogram and find the maximum possible area in the histogram for it. Finally, find the maximum of these values. This will require O(n 2 ).

Problem-25 For Problem-24, can we improve the time complexity?
Solution: Linear search using a stack of incomplete sub problems: There are many ways of solving this problem. Judge has given a nice algorithm for this problem which is based on stack. Process the elements in left-to-right order and maintain a stack of information about started but yet unfinished sub histograms.
If the stack is empty, open a new sub problem by pushing the element onto the stack. Other wise compare it to the element on top of the stack. If the new one is greater we again push it. If the new one is equal we skip it. In all these cases, we continue with the next new element. If the new one is less, we finish the topmost sub problem by updating the maximum area with respect to the element at the top of the stack. Then, we discard the element at the top, and repeat the procedure keeping the current new element.
This way, all sub problems are finished when the stack becomes empty, or its top element is less than or equal to the new element, leading to the actions described above. If all elements have been processed, and the stack is not yet empty, we finish the remaining sub problems by updating the maximum area with respect to the elements at the top.
struct StackItem { int height;
int index;
int MaxRectangleArea(int A[], int n) {
int i, maxArea=-1, top = -1, left, currentArea;
struct Stackltem *S= (struct StackItem *)malloc(sizeof(struct StackItem) * n); for(i=0; i<=n; i++){
while(top >= 0 && (i==n || S[top]-height > A[i])) {
if(top > 0)
left = Stop-11-index;
else left = -1;
currentArea = (i-left-1)* S[top]-height;
--top;
if(currentArea > maxArea)
}
}
if(i<n) {
maxArea currentArea;
++top;
S[top]-height =A[i]; S[top]-index = i;
return maxArea;
At the first impression, this solution seems to be having O(n 2 ) complexity. But if we look carefully, every element is pushed and popped at most once, and in every step of the function at least one element is pushed or popped. Since the amount of work for the decisions and the update is constant, the complexity of the algorithm is O(n) by amortized analysis. Space Complexity: O(n) [for stack].
Problem-26 On a given machine, how do you check whether the stack grows up or down?
Solution: Try noting down the address of a local variable. Call another function with a local variable declared in it and check the address of that local variable and compare
int testStackGrowth() { int temporary; stackGrowth(&temporary);
}
exit(0);
void stackGrowth(int *temp){
int temp2;
printf("\nAddress of first local valuable: %u", temp);
printf("\nAddress of second local: %u", &temp2); if(temp < &temp2)
else
printf("\n Stack is growing downwards");
printf("\n Stack is growing upwards");
Time Complexity: O(1). Space Complexity: O(1)
Problem-27 Given a stack of integers, how do you check whether each successive pair of numbers in the stack is consecutive or not. The pairs can be increasing or decreasing, and if the stack has an odd number of elements, the element at the top is left out of a pair. For example, if the stack of elements are [4, 5, -2, -3, 11, 10, 5, 6, 20], then the output should be true because each of the pairs (4, 5), (-2, -3), (11, 10), and (5, 6) consists of consecutive numbers.
Solution: Refer to Queues chapter.
Problem-28 Recursively remove all adjacent duplicates: Given a string of characters, recursively remove adjacent duplicate characters from string. The output string should not have any adjacent duplicates.

Solution: This solution runs with the concept of in-place stack. When element on stack doesn’t match the current character, we add it to stack. When it matches to stack top, we skip characters until the element matches the top of stack and remove the element from stack.
void remove Adjacent Duplicates (char *str){ int stkptr=-1; int i=0;
int len=strlen(str);
while (i<len){
}
if (stkptr == -1 || str[stkptr]!=str[i]){
stkptr++;
strstkptr=str[i];
i++;
}else{
while(i<len&& str[stkptr]==str[i])
i++; stkptr;
str[stkptr+1]='\0';
Time Complexity: O(n). Space Complexity: O(1) as the stack simulation is done inplace.
Problem-29 Given an array of elements, replace every element with nearest greater element on the right of that element.
Solution: One simple approach would involve scanning the array elements and for each of the elements, scan the remaining elements and find the nearest greater element.
void replaceWithNearestGreaterElement(int A[], int n){
int nextNearestGreater = INT_MIN;
int i=0,j=0;
for (i=0; i<n; i++){
next Nearest Greater = -INT_MIN;
for (j=i+1; j<n; j++){
if (A[i] < Aj]){
nextNearestGreater =A[j];
break;
printf("For the element %d, %d is the nearest greater element \n", A[i], nextNearestGreater);
Problem-30 For Problem-29, can we improve the complexity?
Solution: The approach is pretty much similar to Problem-22. Create a stack and push the first element. For the rest of the elements, mark the current element as next Nearest Greater. If stack is not empty, then pop an element from stack and compare it with next Nearest Greater. If next Nearest Greater is greater than the popped element, then next Nearest Greater is the next greater element for the popped element. Keep popping from the stack while the popped element is smaller than next Nearest Greater. next Nearest Greater becomes the next greater element for all such popped elements. If next Nearest Greater is smaller than the popped element, then push the popped element back
void replace With NearestGreaterElement(int A[], int n){
int i=0;
struct Stack *S= CreateStack();
int element, nextNearestGreater; Push(S, A[0]);
for (i=1; i<n;i++){
}
nextNearestGreater = A[i];
if (!IsEmptyStack(S)){
element = Pop(S);
while (element < nextNearest Greater){
printf("For the element %d, %d is the nearest greater element \n", A[i], nextNearest Greater); if(IsEmptyStack(S))
break;
element = Pop(S);
if (element > nextNearestGreater)
Push(S, element);
Push(S, nextNearestGreater);
while (!IsEmptyStack(S)){
element = Pop(S);
next Nearest Greater = -INT_MIN;
printf("For the element %d, %d is the nearest greater element\n", A[i], nextNearestGreater);
Time Complexity: O(n). Space Complexity: O(n).
Problem-31 How to implement a stack which will support following operations in O(1) time complexity?
• Push which adds an element to the top of stack.
• Pop which removes an element from top of stack.
• Find Middle which will return middle element of the stack.
• Delete Middle which will delete the middle element.
Solution: We can use a LinkedList data structure with an extra pointer to the middle element.
Also, we need another variable to store whether the LinkedList has an even or odd number of elements.
• Push: Add the element to the head of the LinkedList. Update the pointer to the middle element according to variable.
• Pop: Remove the head of the LinkedList. Update the pointer to the middle element according to variable.
• Find Middle: Find Middle which will return middle element of the stack.
• Delete Middle: Delete Middle which will delete the middle element use the logic of Problem-43 from Linked Lists chapter.

