
15.1 Introduction
To understand the importance of string algorithms let us consider the case of entering the URL (Uniform To understand the importance of string algorithms let us consider the case of entering the URL (Uniform Resource Locator) in any browser (say, Internet Explorer, Firefox, or Google Chrome). You will observe that after typing the prefix of the URL, a list of all possible URLs is displayed. That means, the browsers are doing some internal processing and giving us the list of matching URLs. This technique is sometimes called auto – completion.
Similarly, consider the case of entering the directory name in the command line interface (in both Windows and UNIX). After typing the prefix of the directory name, if we press the tab button, we get a list of all matched directory names available. This is another example of auto completion.
In order to support these kinds of operations, we need a data structure which stores the string data efficiently. In this chapter, we will look at the data structures that are useful for implementing string algorithms.
We start our discussion with the basic problem of strings: given a string, how do we search a substring (pattern)? This is called a string matching problem. After discussing various string matching algorithms, we will look at different data structures for storing strings.
15.2 String Matching Algorithms
In this section, we concentrate on checking whether a pattern P is a substring of another string T (T stands for text) or not. Since we are trying to check a fixed string P, sometimes these algorithms are called exact string matching algorithms. To simplify our discussion, let us assume that the length of given text T is n and the length of the pattern P which we are trying to match has the length m. That means, T has the characters from 0 to n – 1 (T[0 …n – 1]) and P has the characters from 0 to m – 1 (T[0 …m – 1]). This algorithm is implemented in C + + as strstr().
In the subsequent sections, we start with the brute force method and gradually move towards better algorithms.
• Brute Force Method
• Rabin-Karp String Matching Algorithm
• String Matching with Finite Automata
• KMP Algorithm
• Boyer-Moore Algorithm
• Suffix Trees
15.3 Brute Force Method
In this method, for each possible position in the text T we check whether the pattern P matches or not. Since the length of T is n, we have n – m + 1 possible choices for comparisons. This is because we do not need to check the last m – 1 locations of T as the pattern length is m. The following algorithm searches for the first occurrence of a pattern string P in a text string T.
Algorithm
//Input: Pattern string P[0..m-1], 8 and F //Goal: All valid shifts displayed
Finite AutomataStringMatcher(int P[], int m, F, 8) { q=0;
for (int i = 0; i < m; i++) q-6(q.T[i]);
if(q == m)
printf("Pattern occurs with shift: %d", i-m);
Time Complexity: O((n – m + 1) × m) ≈ O(n × m). Space Complexity: O(1).
15.4 Rabin-Karp String Matching Algorithm
In this method, we will use the hashing technique and instead of checking for each possible position in T, we check only if the hashing of P and the hashing of m characters of T give the same result.
Initially, apply the hash function to the first m characters of T and check whether this result and P’s hashing result is the same or not. If they are not the same, then go to the next character of T and again apply the hash function to m characters (by starting at the second character). If they are the same then we compare those m characters of T with P.
Selecting Hash Function
At each step, since we are finding the hash of m characters of T, we need an efficient hash function. If the hash function takes O(m) complexity in every step, then the total complexity is O(n × m). This is worse than the brute force method because first we are applying the hash function and also comparing.
Our objective is to select a hash function which takes O(1) complexity for finding the hash of m characters of T every time. Only then can we reduce the total complexity of the algorithm. If the hash function is not good (worst case), the complexity of the Rabin-Karp algorithm is O(n – m + 1) × m) ≈ O(n × m). If we select a good hash function, the complexity of the Rabin-Karp algorithm complexity is O(m + n). Now let us see how to select a hash function which can compute the hash of m characters of T at each step in O(1).
For simplicity, let’s assume that the characters used in string T are only integers. That means, all characters in T ∈ {0,1,2,…,9 }. Since all of them are integers, we can view a string of m consecutive characters as decimal numbers. For example, string ′61815′ corresponds to the number 61815. With the above assumption, the pattern P is also a decimal value, and let us assume that the decimal value of P is p. For the given text T[0..n – 1], let t(i) denote the decimal value of length–m substring T[i.. i + m – 1] for i = 0,1, …,n – m– 1. So, t(i) == p if and only if T[i..i + m – 1] == P[0..m – 1].
We can compute p in O(m) time using Horner’s Rule as:
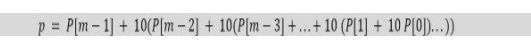
The code for the above assumption is:
int Brute ForceStringMatch (int T[], int n, int P[], int m) { for (int i=0; i<=n-m; i++) { int j=0;
while (j < m && Plj]== Ti + j])
jj+1;
if(j== m) return i;
return -1;
We can compute all t(i), for i = 0,1,…, n – m – 1 values in a total of O(n) time. The value of t(0) can be similarly computed from T[0.. m – 1] in O(m) time. To compute the remaining values t(0), t(1),…, t(n – m – 1), understand that t(i + 1) can be computed from t(i) in constant time.

For example, if T = ″123456″ and m = 3

Step by Step explanation
First : remove the first digit : 123 – 100 * 1 = 23
Second: Multiply by 10 to shift it : 23 * 10 = 230 Third: Add last digit : 230 + 4 = 234
The algorithm runs by comparing, t(i) with p. When t(i) == p, then we have found the substring P in T, starting from position i.
15.5 String Matching with Finite Automata
In this method we use the finite automata which is the concept of the Theory of Computation (ToC). Before looking at the algorithm, first let us look at the definition of finite automata.
Finite Automata
A finite automaton F is a 5-tuple (Q,q0 ,A,∑,δ), where
• Q is a finite set of states
• q0 ∈ Q is the start state
• A ⊆ Q is a set of accepting states
• ∑ is a finite input alphabet
• δ is the transition function that gives the next state for a given current state and input
How does Finite Automata Work?
• The finite automaton F begins in state q0
• Reads characters from ∑ one at a time
• If F is in state q and reads input character a, F moves to state δ(q,d)
• At the end, if its state is in A, then we say, F accepted the input string read so far
• If the input string is not accepted it is called the rejected string
Example: Let us assume that Q = {0,1{,q0 = 0,A = {1},∑ = {a, b}. δ(q,d) as shown in the transition table/diagram. This accepts strings that end in an odd number of a’s; e.g., abbaaa is accepted, aa is rejected.

Important Notes for Constructing the Finite Automata
For building the automata, first we start with the initial state. The FA will be in state k if k characters of the pattern have been matched. If the next text character is equal to the pattern character c, we have matched k + 1 characters and the FA enters state k + 1. If the next text character is not equal to the pattern character, then the FA go to a state 0,1,2,….or k, depending on how many initial pattern characters match the text characters ending with c.
Matching Algorithm
Now, let us concentrate on the matching algorithm.
• For a given pattern P[0.. m – 1], first we need to build a finite automaton F
○ The state set is Q = {0,1,2, …,m}
○ The start state is 0
○ The only accepting state is m
○ Time to build F can be large if ∑ is large
• Scan the text string T[0.. n – 1] to find all occurrences of the pattern P[0.. m – 1]
• String matching is efficient: Θ(n)
○ Each character is examined exactly once
○ Constant time for each character
○ But the time to compute δ (transition function) is O(m|∑|). This is because δ has O(m|∑|) entries. If we assume |∑| is constant then the complexity becomes O(m).
Algorithm:
value = 0;
for (int i=0; i<m-1; i++) { value value* 10; value = value + P[i];
Time Complexity: O(m).
15.6 KMP Algorithm
As before, let us assume that T is the string to be searched and P is the pattern to be matched. This algorithm was presented by Knuth, Morris and Pratt. It takes O(n) time complexity for searching a pattern. To get O(n) time complexity, it avoids the comparisons with elements of T that were previously involved in comparison with some element of the pattern P.
The algorithm uses a table and in general we call it prefix function or prefix table or fail function F. First we will see how to fill this table and later how to search for a pattern using this table. The prefix function F for a pattern stores the knowledge about how the pattern matches against shifts of itself. This information can be used to avoid useless shifts of the pattern P. It means that this table can be used for avoiding backtracking on the string T.
Prefix Table
int Fl]; //assume F is a global array void Prefix-Table(int P[], int m) { int i=1,j=0, F[0]=0; while(i<m) {
if(P[i]==Pij]){
Fil-j+1;
i++;
}
j++;
else if(j>0)
else {
j-Fj-1];
Fli=0;
i++;
As an example, assume that P = a b a b a c a. For this pattern, let us follow the step-by-step instructions for filling the prefix table F. Initially: m = length[P] = 7,F[0] = 0 and F[1] = 0.


At this step the filling of the prefix table is complete.
Matching Algorithm
The KMP algorithm takes pattern P, string T and prefix function F as input, and finds a match of Pin T.
int KMP(char T[], int n, int P[], int m) { int i=0,j=0; Prefix-Table(P,m);
while(i<n) {
if(T[i]==P]){
if(j=-m-1)
return i-j;
else{
i++;
j++;
}
}
else if(j>0)
j-Fj-1];
else
i++;
return -1;
Time Complexity: O(m + n), where m is the length of the pattern and n is the length of the text to be searched. Space Complexity: O(m).
Now, to understand the process let us go through an example. Assume that T = b a c b a b a b a b a c a c a & P = a b a b a c a. Since we have already filled the prefix table, let us use it and go to the matching algorithm. Initially: n = size of T = 15; m = size of P = 7.
Step 1: i = 0, j = 0, comparing P[0] with T[0]. P[0] does not match with T[0]. P will be shifted one position to the right.



Notes:
• KMP performs the comparisons from left to right
• KMP algorithm needs a preprocessing (prefix function) which takes O(m) space and time complexity
• Searching takes O(n + m) time complexity (does not depend on alphabet size)
15.7 Boyer-Moore Algorithm
Like the KMP algorithm, this also does some pre-processing and we call it last function. The algorithm scans the characters of the pattern from right to left beginning with the rightmost character. During the testing of a possible placement of pattern P in T, a mismatch is handled as follows: Let us assume that the current character being matched is T[i] = c and the corresponding pattern character is P[j]. If c is not contained anywhere in P, then shift the pattern P completely past T[i]. Otherwise, shift P until an occurrence of character c in P gets aligned with T[i]. This technique avoids needless comparisons by shifting the pattern relative to the text.
The last function takes O(m + |∑|) time and the actual search takes O(nm) time. Therefore the worst case running time of the Boyer-Moore algorithm is O(nm + |∑|). This indicates that the worst-case running time is quadratic, in the case of n == m, the same as the brute force algorithm.
• The Boyer-Moore algorithm is very fast on the large alphabet (relative to the length of the pattern).
• For the small alphabet, Boyer-Moore is not preferable.
• For binary strings, the KMP algorithm is recommended.
• For the very shortest patterns, the brute force algorithm is better.
15.8 Data Structures for Storing Strings
If we have a set of strings (for example, all the words in the dictionary) and a word which we want to search in that set, in order to perform the search operation faster, we need an efficient way of storing the strings. To store sets of strings we can use any of the following data structures.
• Hashing Tables
• Binary Search Trees
• Tries
• Ternary Search Trees
15.9 Hash Tables for Strings
As seen in the Hashing chapter, we can use hash tables for storing the integers or strings. In this case, the keys are nothing but the strings. The problem with hash table implementation is that we lose the ordering information – after applying the hash function, we do not know where it will map to. As a result, some queries take more time. For example, to find all the words starting with the letter “K”, with hash table representation we need to scan the complete hash table. This is because the hash function takes the complete key, performs hash on it, and we do not know the location of each word.
15.10 Binary Search Trees for Strings
In this representation, every node is used for sorting the strings alphabetically. This is possible because the strings have a natural ordering: A comes before B, which comes before C, and so on. This is because words can be ordered and we can use a Binary Search Tree (BST) to store and retrieve them. For example, let us assume that we want to store the following strings using BSTs:
this is a career monk string
For the given string there are many ways of representing them in BST. One such possibility is shown in the tree below.

Issues with Binary Search Tree Representation
This method is good in terms of storage efficiency. But the disadvantage of this representation is that, at every node, the search operation performs the complete match of the given key with the node data, and as a result the time complexity of the search operation increases. So, from this we can say that BST representation of strings is good in terms of storage but not in terms of time.
15.11 Tries
Now, let us see the alternative representation that reduces the time complexity of the search operation. The name trie is taken from the word re”trie”.
What is a Trie?
A trie is a tree and each node in it contains the number of pointers equal to the number of characters of the alphabet. For example, if we assume that all the strings are formed with English alphabet characters “a” to “z” then each node of the trie contains 26 pointers. A trie data structure can be declared as:
struct TrieNode{
}
char data;
int is_End_Of_String;
// Contains the current node character. // Indicates whether the string formed from root to // current node is a string or not
struct TrieNode *child[26]; // Pointers to other tri nodes
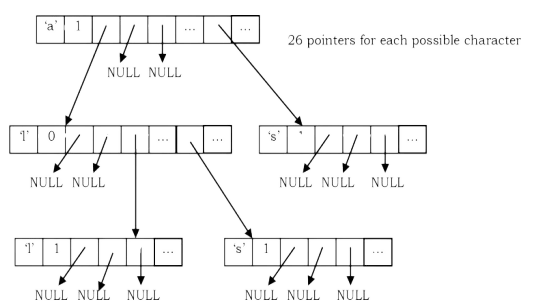
Suppose we want to store the strings “a”,”all”,”als”, and “as”“: trie for these strings will look like:
Why Tries?
The tries can insert and find strings in O(L) time (where L represents the length of a single word). This is much faster than hash table and binary search tree representations.
Trie Declaration
The structure of the TrieNode has data (char), is_End_Of_String (boolean), and has a collection of child nodes (Collection of TrieNodes). It also has one more method called subNode(char). This method takes a character as argument and will return the child node of that character type if that is present. The basic element – TrieNode of a TRIE data structure looks like this:
struct TrieNode{ char data;
};
int is_End_Of_String;
struct TrieNode *child[];
struct TrieNode TrieNode subNode(struct TrieNode "root, char c){
if(root!= NULL){
for(int i=0; i < 26; i++){
if(root.child[i]-data == c) return root.child([i];
}
}
return NULL;
Now that we have defined our TrieNode, let’s go ahead and look at the other operations of TRIE. Fortunately, the TRIE data structure is simple to implement since it has two major methods: insert() and search(). Let’s look at the elementary implementation of both these methods.
Inserting a String in Trie
To insert a string, we just need to start at the root node and follow the corresponding path (path from root indicates the prefix of the given string). Once we reach the NULL pointer, we just need to create a skew of tail nodes for the remaining characters of the given string.
void InsertInTrie(struct TrieNode *root, char *word) {
if(!*word) return; if(!root) {
}
struct TrieNode *newNode = (struct TrieNode *) malloc (sizeof(struct TrieNode *));
newNode-data="word;
for(int i=0; i<26; i++) newNode-child[i]=NULL;
if(!*(word+1))
newNode-is_End_Of_String = 1;
else newNode-child['word] = InsertInTrie(newNode-child[*word], word+1); return newNode;
root-child("word] = InsertInTrie(root-child["word], word+1);
return root;
Time Complexity: O(L), where L is the length of the string to be inserted.
Note: For real dictionary implementation, we may need a few more checks such as checking whether the given string is already there in the dictionary or not.
Searching a String in Trie
The same is the case with the search operation: we just need to start at the root and follow the pointers. The time complexity of the search operation is equal to the length of the given string that want to search.
int SearchInTrie(struct TrieNode *root, char *word){
if(!root)
return -1;
if(!*word){
if(root- is_End_Of_String) return 1;
else return -1;
if(root-data == "word)
return SearchInTrie(root-child['word], word+1); else return -1;
Time Complexity: O(L), where L is the length of the string to be searched.
Issues with Tries Representation
The main disadvantage of tries is that they need lot of memory for storing the strings. As we have seen above, for each node we have too many node pointers. In many cases, the occupancy of each node is less. The final conclusion regarding tries data structure is that they are faster but require huge memory for storing the strings.
Note: There are some improved tries representations called trie compression techniques. But, even with those techniques we can reduce the memory only at the leaves and not at the internal nodes.
15.12 Ternary Search Trees
This representation was initially provided by Jon Bentley and Sedgewick. A ternary search tree takes the advantages of binary search trees and tries. That means it combines the memory efficiency of BSTs and the time efficiency of tries.
Ternary Search Trees Declaration

The Ternary Search Tree (TST) uses three pointers:
• The left pointer points to the TST containing all the strings which are alphabetically less than data.
• The right pointer points to the TST containing all the strings which are alphabetically greater than data.
• The eq pointer points to the TST containing all the strings which are alphabetically equal to data. That means, if we want to search for a string, and if the current character of the input string and the data of current node in TST are the same, then we need to proceed to the next character in the input string and search it in the subtree which is pointed by eq.
Inserting strings in Ternary Search Tree
For simplicity let us assume that we want to store the following words in TST (also assume the same order): boats, boat, bat and bats. Initially, let us start with the boats string.

Now if we want to insert the string boat, then the TST becomes [the only change is setting the is_End_Of_String flag of “t” node to 1]:

Now, let us insert the next string: bat
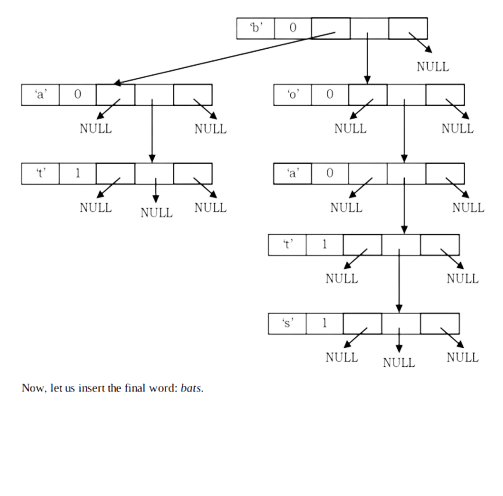
Now, let us insert the final word: bats
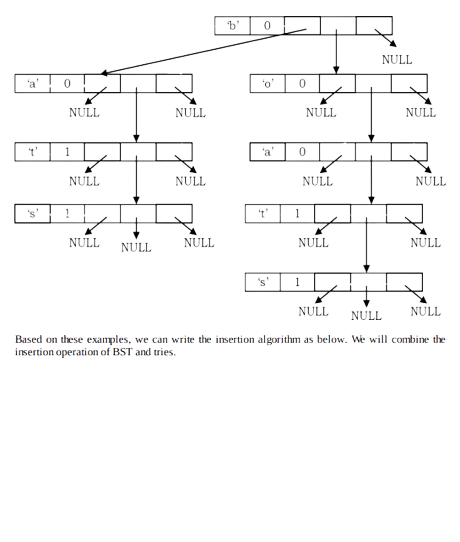
Based on these examples, we can write the insertion algorithm as below. We will combine the
insertion operation of BST and tries.
struct TSTNode *InsertInTST(struct TSTNode *root, char *word) { if(root == NULL) {
root (struct TSTNode *)malloc(sizeof(struct TSTNode)); root-data = "word;
root-is_End_Of_String = 1;
root-left = root-eq = root-right = NULL;
if("word < root-data)
}
root-left InsertInTST (root-left, word);
else if(*word == root-data) {
if(*(word+1))
root-eq InsertInTST (root-eq, word+1); else root-is_End_Of_String = 1;
else root-right InsertInTST (root-right, word);
return root;
Time Complexity: O(L), where L is the length of the string to be inserted.
Searching in Ternary Search Tree
If after inserting the words we want to search for them, then we have to follow the same rules as that of binary search. The only difference is, in case of match we should check for the remaining characters (in eq subtree) instead of return. Also, like BSTs we will see both recursive and nonrecursive versions of the search method.
int SearchInTSTRecursive(struct TSTNode *root, char *word){
if(!root) return -1;
if("word < root-data)
}
}
return SearchInTSTRecursive(root-left, word); else if("word> root-data)
return SearchInTSTRecursive(root-right, word);
else {
if(root-is_End_Of_String && "(word+1)==0) return 1;
return SearchinTSTRecursive(root-eq, ++word);
int SearchinTSTNon-Recursive(struct TSTNode *root, char *word) {
while (root) {
if("word < root-data)
root = root-left;
else if("word=root-data) {
if(root-is_End_Of_String &&*(word+1) == 0)
return 1;
word++;
root = root-eq;
}
else root root-right;
}
return -1;
Time Complexity: O(L), where L is the length of the string to be searched.
Displaying All Words of Ternary Search Tree
If we want to print all the strings of TST we can use the following algorithm. If we want to print them in sorted order, we need to follow the inorder traversal of TST.
char word[1024];
void DisplayAllWords(struct TSTNode *root) {
if(!root)
return;
DisplayAllWords(root-left); word[i] = root-data;
if(root-is_End_Of_String) { word[i] = '\0';
}
printf("%c", word);
DisplayAllWords(root-eq);
i--;
DisplayAllWords(root-right);
Finding the Length of the Largest Word in TST
This is similar to finding the height of the BST and can be found as:
int MaxLengthOfLargestWordInTST(struct TSTNode *root) {
if(!root)
return 0;
return Max(MaxLength OfLargest WordInTST(root-left),
MaxLengthOfLargest Word InTST(root-eq)+1,
MaxLengthOfLargest WordInTST(root-right));
15.13 Comparing BSTs, Tries and TSTs
• Hash table and BST implementation stores complete the string at each node. As a result they take more time for searching. But they are memory efficient.
• TSTs can grow and shrink dynamically but hash tables resize only based on load factor.
• TSTs allow partial search whereas BSTs and hash tables do not support it.
• TSTs can display the words in sorted order, but in hash tables we cannot get the sorted order.
• Tries perform search operations very fast but they take huge memory for storing the string.
• TSTs combine the advantages of BSTs and Tries. That means they combine the memory efficiency of BSTs and the time efficiency of tries
15.14 Suffix Trees
Suffix trees are an important data structure for strings. With suffix trees we can answer the queries very fast. But this requires some preprocessing and construction of a suffix tree. Even though the construction of a suffix tree is complicated, it solves many other string-related problems in linear time.
Note: Suffix trees use a tree (suffix tree) for one string, whereas Hash tables, BSTs, Tries and TSTs store a set of strings. That means, a suffix tree answers the queries related to one string. Let us see the terminology we use for this representation.
Prefix and Suffix
Given a string T = T1T2 … Tn , the prefix of T is a string T1 …Ti where i can take values from 1 to n. For example, if T = banana, then the prefixes of T are: b, ba, ban, bana, banan, banana.
Similarly, given a string T = T1T2 … Tn , the suffix of T is a string Ti …Tn where i can take values from n to 1. For example, if T = banana, then the suffixes of T are: a, na, ana, nana, anana, banana. Observation From the above example, we can easily see that for a given text T and pattern P, the exact string matching problem can also be defined as:
• Find a suffix of T such that P is a prefix of this suffix or
• Find a prefix of T such that P is a suffix of this prefix.
Example: Let the text to be searched be T = acebkkbac and the pattern be P = kkb. For this example, P is a prefix of the suffix kkbac and also a suffix of the prefix acebkkb.
What is a Suffix Tree?
In simple terms, the suffix tree for text T is a Trie-like data structure that represents the suffixes of T. The definition of suffix trees can be given as: A suffix tree for a n character string T[1 …n] is a rooted tree with the following properties.
• A suffix tree will contain n leaves which are numbered from 1 to n
• Each internal node (except root) should have at least 2 children
• Each edge in a tree is labeled by a nonempty substring of T
• No two edges of a node (children edges) begin with the same character
• The paths from the root to the leaves represent all the suffixes of T
The Construction of Suffix Trees
Algorithm
1. Let S be the set of all suffixes of T. Append $ to each of the suffixes.
2. Sort the suffixes in S based on their first character.
3. For each group Sc (c ∈ ∑):
(i) If Sc group has only one element, then create a leaf node.
(ii) Otherwise, find the longest common prefix of the suffixes in Sc group, create an internal node, and recursively continue with Step 2, S being the set of remaining suffixes from Sc after splitting off the longest common prefix.
For better understanding, let us go through an example. Let the given text be T = tatat. For this string, give a number to each of the suffixes.
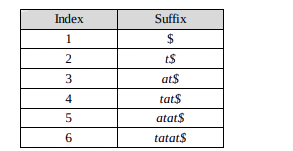
Now, sort the suffixes based on their initial characters.

In the three groups, the first group has only one element. So, as per the algorithm, create a leaf node for it, as shown below.
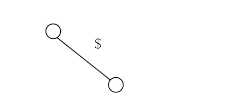
Now, for S2 and S3 (as they have more than one element), let us find the longest prefix in the group, and the result is shown below.

For S2 and S3 , create internal nodes, and the edge contains the longest common prefix of those groups.
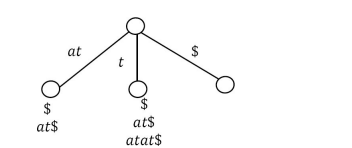
Now we have to remove the longest common prefix from the S2 and S3 group elements.

Out next step is solving S2 and S3 recursively. First let us take S2 . In this group, if we sort them based on their first character, it is easy to see that the first group contains only one element $, and the second group also contains only one element, at$. Since both groups have only one element, we can directly create leaf nodes for them.

At this step, both S1 and S2 elements are done and the only remaining group is S3 . As similar to earlier steps, in the S3 group, if we sort them based on their first character, it is easy to see that there is only one element in the first group and it is $. For S3 remaining elements, remove the longest common prefix.

In the S3 second group, there are two elements: $ and at$. We can directly add the leaf nodes for the first group element $. Let us add S3 subtree as shown below.

Now, S3 contains two elements. If we sort them based on their first character, it is easy to see that there are only two elements and among them one is $ and other is at$. We can directly add the leaf nodes for them. Let us add S3 subtree as shown below.
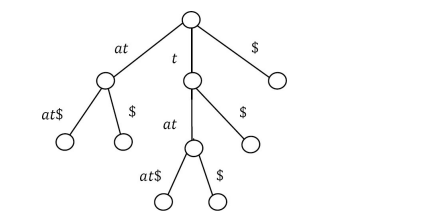
Since there are no more elements, this is the completion of the construction of the suffix tree for string T = tatat. The time-complexity of the construction of a suffix tree using the above algorithm is O(n 2 ) where n is the length of the input string because there are n distinct suffixes. The longest has length n, the second longest has length n – 1, and so on.
Note:
• There are O(n) algorithms for constructing suffix trees.
• To improve the complexity, we can use indices instead of string for branches.
Applications of Suffix Trees
All the problems below (but not limited to these) on strings can be solved with suffix trees very efficiently (for algorithms refer to Problems section).
• Exact String Matching: Given a text T and a pattern P, how do we check whether P appears in T or not?
• Longest Repeated Substring: Given a text T how do we find the substring of T that is the maximum repeated substring?
• Longest Palindrome: Given a text T how do we find the substring of T that is the longest palindrome of T?
• Longest Common Substring: Given two strings, how do we find the longest common substring?
• Longest Common Prefix: Given two strings X[i …n] and Y[j …m],how do we find the longest common prefix?
• How do we search for a regular expression in given text T?
• Given a text T and a pattern P, how do we find the first occurrence of P in T?
15.15 String Algorithms: Problems & Solutions
Problem-1 Given a paragraph of words, give an algorithm for finding the word which appears the maximum number of times. If the paragraph is scrolled down (some words disappear from the first frame, some words still appear, and some are new words), give the maximum occurring word. Thus, it should be dynamic.
: Solution For this problem we can use a combination of priority queues and tries. We start by creating a trie in which we insert a word as it appears, and at every leaf of trie. Its node contains that word along with a pointer that points to the node in the heap [priority queue] which we also create. This heap contains nodes whose structure contains a counter. This is its frequency and also a pointer to that leaf of trie, which contains that word so that there is no need to store the word twice.
Whenever a new word comes up, we find it in trie. If it is already there, we increase the frequency of that node in the heap corresponding to that word, and we call it heapify. This is done so that at any point of time we can get the word of maximum frequency. While scrolling, when a word goes out of scope, we decrement the counter in heap. If the new frequency is still greater than zero, heapify the heap to incorporate the modification. If the new frequency is zero, delete the node from heap and delete it from trie.
Problem-2 Given two strings, how can we find the longest common substring?
Solution: Let us assume that the given two strings are T1 and T2 . The longest common substring of two strings, T1 and T2 , can be found by building a generalized suffix tree for T1 and T2 . That means we need to build a single suffix tree for both the strings. Each node is marked to indicate if it represents a suffix of T1 or T2 or both. This indicates that we need to use different marker symbols for both the strings (for example, we can use $ for the first string and # for the second symbol). After constructing the common suffix tree, the deepest node marked for both T1 and T2 represents the longest common substring.
Another way of doing this is: We can build a suffix tree for the string T1$T2#. This is equivalent to building a common suffix tree for both the strings.
Time Complexity: O(m + n), where m and n are the lengths of input strings T1 and T2 .
Problem-3 Longest Palindrome: Given a text T how do we find the substring of T which is the longest palindrome of T?
Solution: The longest palindrome of T[1..n] can be found in O(n) time. The algorithm is: first build a suffix tree for T$reverse(T)# or build a generalized suffix tree for T and reverse(T). After building the suffix tree, find the deepest node marked with both $ and #. Basically it means find the longest common substring.
Problem-4 Given a string (word), give an algorithm for finding the next word in the dictionary.
Solution: Let us assume that we are using Trie for storing the dictionary words. To find the next word in Tries we can follow a simple approach as shown below. Starting from the rightmost character, increment the characters one by one. Once we reach Z, move to the next character on the left side.
Whenever we increment, check if the word with the incremented character exists in the dictionary or not. If it exists, then return the word, otherwise increment again. If we use TST, then we can find the inorder successor for the current word.
Problem-5 Give an algorithm for reversing a string.
Solution:
//If the str is editable
char *ReversingString(char str[]) { char temp, start, end;
if(str == NULL || *str ==
return str;
-'10)
for (end = 0; str[end]; end++); end--;
for (start = 0; start < end; start++, end--) {
}
temp = str[start]; str[start] = str[end]; str[end] = temp;
return str;
Time Complexity: O(n), where n is the length of the given string. Space Complexity: O(n).
Problem-6 If the string is not editable, how do we create a string that is the reverse of the given string?
Solution: If the string is not editable, then we need to create an array and return the pointer of that.
//If str is a const string (not editable) char ReversingString(char* str) { int start, end, len;
char temp, *ptr=NULL; len-strlen(str);
}
ptr-malloc(sizeof(char)*(len+1));
ptr strcpy(ptr,str);
for (start=0, end-len-1; start<=end; start++, end--) { temp-ptr[start]; ptr[start]=ptr[end]; ptr[end]=temp;
return ptr;
//Swapping
Time Complexity: O(n/2)=O(n), where n is the length of the given string. Space Complexity: O(1).
Problem-7 Can we reverse the string without using any temporary variable?
Solution: Yes, we can use XOR logic for swapping the variables.
char ReversingString(char *str) {
int start 0, end= strlen(str)-1; while(start<end) {
Λα
str[start] str[end]; str[end] ^ str[start]; str[start]^= str[end];
++start; --end;
}
return str;
Time Complexity: O(n/2)=O(n), where n is the length of the given string. Space Complexity: O(1).
Problem-8 Given a text and a pattern, give an algorithm for matching the pattern in the text. Assume ? (single character matcher) and * (multi character matcher) are the wild card characters.
Solution: Brute Force Method. For efficient method, refer to the theory section.
int PatternMatching(char *text, char *pattern) {
if('pattern == 0) return 1;
if("text == 0)
return *p == 0;
if('?'*pattern)
return PatternMatching(text+1,pattern+1) | | PatternMatching(text,pattern+1); if *pattern)
return PatternMatching(text+1,pattern) || Pattern Matching(text,pattern+1); if("text == *pattern)
return PatternMatching(text+1,pattern+1);
return -1;
Time Complexity: O(mn), where m is the length of the text and n is the length of the pattern. Space Complexity: O(1).
Problem-9 Give an algorithm for reversing words in a sentence. Example: Input: “This is a Career Monk String”, Output: “String Monk Career a is This”
Solution: Start from the beginning and keep on reversing the words. The below implementation assumes that ‘ ‘ (space) is the delimiter for words in given sentence.
void ReverseWordsInSentences(char *text) { int wordStart, wordEnd, length; length = strlen(text);
ReversingString(text, 0, length-1);
for(wordStart=wordEnd = 0; word End < length; wordEnd ++) { if(text[wordEnd]!=''){
wordStart = wordEnd;
while (text[wordEnd] != '' && wordEnd < length) wordEnd ++;
word End--;
ReversingString(text, wordStart, wordEnd); // Found current word, reverse it now.
}
}
void ReversingString(char text[], int start, int end) { for (char temp; start < end; start++, end--) {
temp = str[end]; str[end]= str[start];
strstart] = temp;
Time Complexity: O(2n) ≈ O(n), where n is the length of the string. Space Complexity: O(1).
Problem-10 Permutations of a string [anagrams]: Give an algorithm for printing all possible permutations of the characters in a string. Unlike combinations, two permutations are considered distinct if they contain the same characters but in a different order. For simplicity assume that each occurrence of a repeated character is a distinct character. That is, if the input is “aaa”, the output should be six repetitions of “aaa”. The permutations may be output in any order.
Solution: The solution is reached by generating n! strings, each of length n, where n is the length of the input string.
void Permutations (int depth, char *permutation, int *used, char *original) {
int length = strlen(original);
if(depth == length)
else{
printf("%s", permutation);
for (int i=0; i < length; i++) { if(!used[i]) {
used[i] = 1;
permutation[depth] = original[i];
Permutations(depth + 1, permutation, used, original);
used[i] = 0;
Problem-11 Combinations Combinations of a String: Unlike permutations, two combinations are considered to be the same if they contain the same characters, but may be in a different order. Give an algorithm that prints all possible combinations of the characters in a string. For example, “ac” and “ab” are different combinations from the input string “abc”, but “ab” is the same as “ba”.
Solution: The solution is achieved by generating n!/r! (n – r)! strings, each of length between 1 and n where n is the length of the given input string.
Algorithm: For each of the input characters a. Put the current character in output string and print it. b. If there are any remaining characters, generate combinations with those remaining characters.
void Combinations(int depth, char *combination, int start, char *original) {
int length = strlen(original); for (int i = start; i < length; i++) { combination[depth] original[i]; combination[depth+1] = '\0'; printf("%s", combination); if(i < length-1)
Combinations(depth + 1, combination, start + 1, original);
Problem-12 Given a string “ABCCBCBA”, give an algorithm for recursively removing the adjacent characters if they are the same. For example, ABCCBCBA nnnnnn> ABBCBA- >ACBA
Solution: First we need to check if we have a character pair; if yes, then cancel it. Now check for next character and previous element. Keep canceling the characters until we either reach the start of the array, reach the end of the array, or don’t find a pair.
void RremoveAdjacent Pairs(char* str) { int len = strlen(str), i, j = 0; for (i=1; i <= len; i++){
}
}
return;
while ((str[i]== str[j]) && (>= 0)){
i++;
j-;
str[++] = str[i];
//Cancel pairs
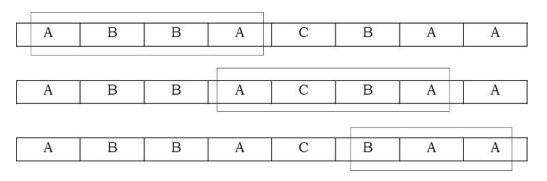
Problem-13 Given a set of characters CHARS and a input string INPUT, find the minimum window in str which will contain all the characters in CHARS in complexity O(n). For example, INPUT = ABBACBAA and CHARS = AAB has the minimum window BAA.
Solution: This algorithm is based on the sliding window approach. In this approach, we start from the beginning of the array and move to the right. As soon as we have a window which has all the required elements, try sliding the window as far right as possible with all the required elements. If the current window length is less than the minimum length found until now, update the minimum length. For example, if the input array is ABBACBAA and the minimum window should cover characters AAB, then the sliding window will move like this:
Algorithm: The input is the given array and chars is the array of characters that need to be found.
1 Make an integer array shouldfind[] of len 256. The i th element of this array will have the count of how many times we need to find the element of ASCII value i.
2 Make another array hasfound of 256 elements, which will have the count of the required elements found until now.
3 Count <= 0 4 While input[i]
a. If input[i] element is not to be found→ continue
b. If input[i] element is required => increase count by 1.
c. If count is length of chars[] array, slide the window as much right as possible.
d. If current window length is less than min length found until now, update min length.
#define MAX 256
void MinLengthWindow(char input[], char chars[]) {
int shouldfind[MAX] = (0,), hasfound [MAX] = (0,); int j=0, cnt = 0, start=0, finish, minwindow INT_MAX; int charlen strlen(chars), iplen strlen(input); for (int i=0; i< charlen; i++)
.
shouldfind[chars[i]] += 1;
finish = iplen;
for (int i=0; i< iplen; i++) {
if(!shouldfind[input[i]])
continue;
hasfound input[i] += 1;
if(should find input[i]]>= hasfound [input[i]])
cnt++;
if(cnt == charlen) {
while (shouldfind input[j]]== 0 || hasfound[input[ij]]> shouldfind[input[j]]] if has found input[j]]> shouldfind[input[j]])
j++;
}
hasfound input[j]]--;
if(minwindow (i-j+1)) {
minwindow i-j+1;
finish = i;
start = j;
}
}
printf("Start: %d and Finish: %d", start, finish);
Complexity: If we walk through the code, i and j can traverse at most n steps (where n is the input size) in the worst case, adding to a total of 2n times. Therefore, time complexity is O(n).
Problem-14 We are given a 2D array of characters and a character pattern. Give an algorithm to find if the pattern is present in the 2D array. The pattern can be in any order (all 8 neighbors to be considered) but we can’t use the same character twice while matching. Return 1 if match is found, 0 if not. For example: Find “MICROSOFT” in the below matrix.

Solution: Manually finding the solution of this problem is relatively intuitive; we just need to describe an algorithm for it. Ironically, describing the algorithm is not the easy part.
How do we do it manually? First we match the first element, and when it is matched we match the second element in the 8 neighbors of the first match. We do this process recursively, and when the last character of the input pattern matches, return true.
During the above process, take care not to use any cell in the 2D array twice. For this purpose, you mark every visited cell with some sign. If your pattern matching fails at some point, start matching from the beginning (of the pattern) in the remaining cells. When returning, you unmark the visited cells.
Let’s convert the above intuitive method into an algorithm. Since we are doing similar checks for pattern matching every time, a recursive solution is what we need. In a recursive solution, we need to check if the substring passed is matched in the given matrix or not. The condition is not to use the already used cell, and to find the already used cell, we need to add another 2D array to the function (or we can use an unused bit in the input array itself.) Also, we need the current position of the input matrix from where we need to start. Since we need to pass a lot more information than is actually given, we should be having a wrapper function to initialize the extra information to be passed.
Algorithm:
If we are past the last character in the pattern
Return true
If we get a used cell again
Return false
if we got past the 2D matrix
Return false
If searching for first element and cell doesn’t match
FindMatch with next cell in row-first order (or column-first order)
Otherwise if character matches
mark this cell as used
res = FindMatch with next position of pattern in 8 neighbors
mark this cell as unused
Return res
Otherwise
Return false
}
#define MAX 100
boolean FindMatch_wrapper(char mat[MAX][MAX], char *pat, int nrow, int ncol) { if(strlen(pat)>nrow*ncol) return false;
int used[MAX][MAX] {{0});
return FindMatch(mat, pat, used, 0, 0, nrow, ncol, 0);
//level: index till which pattern is matched & x, y: current position in 2D array boolean FindMatch(char mat[MAX][MAX], char *pat, int used[MAX][MAX],
int x, int y, int nrow, int ncol, int level) {
if(level == strlen(pat)) //pattern matched
}
return true;
if(nrow=x | | ncol=y) return false;
if(used[x][y])
return false;
if(mat[x][y] != pat[level] && level == 0) {
if(x < (nrow -1))
return FindMatch(mat, pat, used, x+1, y, nrow, ncol, level); //next element in same row else ifly < (ncol-1))
return FindMatch(mat, pat, used, 0, y+1, nrow, ncol, level); //first element from same column else return false;
else if(mat[x][y]== pat[level]) {
boolean res;
used[x][y]= 1;
//marking this cell as used
//finding subpattern in 8 neighbors
res = (x>0 ? FindMatch(mat, pat, used, x-1, y, nrow, ncol, level+1): false) || (res = x < (nrow - 1) ? Find Match(mat, pat, used, x+1, y, nrow, ncol, level+1): false) ||
(res = y> 0? FindMatch(mat, pat, used, x, y-1, nrow, ncol, level+1): false) ||
(res y < (ncol 1)? FindMatch(mat, pat, used, x, y+1, nrow, ncol, level+1): false) ||
(res = x < (nrow - 1)&&(y <ncol -1)?FindMatch(mat, pat, used, x+1, y+1, nrow, ncol, level+1): false) || (res = x < (nrow - 1) && y> 0? FindMatch(mat, pat, used, x+1, y-1, nrow, ncol, level+1): false) || <(ncol-1)? FindMatch(mat, pat, used, x-1, y+1, nrow, ncol, level+1): false) || (res = x > 0 && y > 0? FindMatch(mat, pat, used, x-1, y-1, nrow, ncol, level+1): false);
(res = x>0&& y < (
used[x][y]= 0;
return res;
//marking this cell as unused
}
else return false;
Problem-15 Given two strings str1 and str2, write a function that prints all interleavings of the given two strings. We may assume that all characters in both strings are different. Example: Input: str1 = “AB”, str2 = “CD” and Output: ABCD ACBD ACDB CABD CADB CDAB. An interleaved string of given two strings preserves the order of characters in individual strings. For example, in all the interleavings of above first example, ‘A’ comes before ‘B’ and ‘C comes before ‘D’.
Solution: Let the length of str1 be m and the length of str2 be n. Let us assume that all characters in str1 and str2 are different. Let Count(m,n) be the count of all interleaved strings in such strings. The value of Count(m,n) can be written as follow

To print all interleavings, we can first fix the first character of strl[0..m-1] in output string, and recursively call for str1[1..m-1] and str2[0..n-1]. And then we can fix the first character of str2[0..n-1] and recursively call for str1[0..m-1] and str2[1..n-1].
void PrintInterleavings(char *str1, char *str2, char *iStr, int m, int n, int i){
}
}
// Base case: If all characters of strl & str2 have been included in output string, // then print the output string
if (m==0 && n ==0) printf("%s\n", iStr);
// If some characters of strl are left to be included, then include the // first character from the remaining characters and recur for rest if (m != 0) {
iStr[i] = str1[0];
PrintInterleavings(str1+ 1, str2, iStr, m-1, n, i+1);
// If some characters of str2 are left to be included, then include the // first character from the remaining characters and recur for rest if (n =0){
iStr[i] = str2[0];
PrintInterleavings(str1, str2+1, iStr, m, n-1, i+1);
// Allocates memory for output string and uses PrintInterleavings() for printing all interleaving's void Print(char *strl, char *str2, int m, int n){
// allocate memory for the output string char *iStr= (char*)malloc((m+n+1)* sizeof(char)); // Set the terminator for the output string iStr[m+n] = '\0';
// print all interleaving's using PrintInterleavings() PrintInterleavings(str1, str2, iStr, m, n, 0);
free(iStr);
Problem-16 Given a matrix with size n × n containing random integers. Give an algorithm which checks whether rows match with a column(s) or not. For example, if i th row matches with j th column, and i th row contains the elements – [2,6,5,8,9]. Then;’’ 1 column would also contain the elements – [2,6,5,8,9].
Solution: We can build a trie for the data in the columns (rows would also work). Then we can compare the rows with the trie. This would allow us to exit as soon as the beginning of a row does not match any column (backtracking). Also this would let us check a row against all columns in one pass. If we do not want to waste memory for empty pointers then we can further improve the solution by constructing a suffix tree.
Problem-17 Write a method to replace all spaces in a string with ‘%20’. Assume string has sufficient space at end of string to hold additional characters.
Solution: Find the number of spaces. Then, starting from end (assuming string has enough space), replace the characters. Starting from end reduces the overwrites.
void encodeSpaceWithString(char* A){ char *space = "%20"; int stringLengthstrlen(A); if(stringLength ==0){ return;
}
int i, numberOfSpaces = 0; for(i=0; i< stringLength; i++){ if(A[i]==''|| A[i]=='\t'){
}
numberOfSpaces ++;
if(!numberOfSpaces)
return;
int newLength = len + numberOfSpaces * 2; A[newLength] = '\0';
for(i= stringLength-1; i >= 0; i--){ if(A[i]==''|| A[i]=='\t'){
A[newLength--] = '0'; A[newLength--] = '2'; A[newLength---"%';
}
else
A[newLength--] = A[i];
Time Complexity: O(n). Space Complexity: O(1). Here, we do not have to worry about the space needed for extra characters.
Problem-18 Running length encoding: Write an algorithm to compress the given string by using the count of repeated characters and if new corn-pressed string length is not smaller than the original string then return the original string.
Solution:
With extra space of O(2):
string CompressString(string inputStr){ char last = inputStr.at(0);
int size = 0, count = 1;
char temp[2]; string str;
for (int i=1; i < inputStr.length(); i++){
if(last == inputStr.at(i))
else{
count++;
itoa(count, temp, 10);
str += last;
str += temp;
last = inputStr.at(i);
count = 1;
}
str = str+last+ temp;
// If the compresed string size is greater than input string, return input string
if(str.length() >= inputStr.length())
return inputStr;
else return str;
Time Complexity: O(n). Space Complexity: O(1), but it uses a temporary array of size two.
Without extra space (inplace):
char CompressString(char *inputStr, char currentChar, int lengthIndex, int& countChar, int& index){ if(lengthIndex == -1)
}
return currentChar;
char lastChar CompressString(inputStr, inputStr[lengthIndex], lengthIndex-1, countChar, index); if(lastChar == currentChar)
else {
countChar++;
inputStr[index++] = lastChar;
for(int i=0; i< NumToString(countChar).length(); i++) inputStr[index++] NumToString(countChar).at(i);
countChar = 1;
return currentChar;
Time Complexity: O(n). Space Complexity: O(1)

